基于110t拼装式起重船的结构强度与浮箱体拼装优化研究

李爱华

（上海交通大学船舶海洋与建筑工程学院，上海 200240）

基于110t拼装式起重船的结构强度与浮箱体拼装优化研究

李爱华

（上海交通大学船舶海洋与建筑工程学院，上海 200240）

文章针对某110t拼装式起重船，研究其两侧增设首尾浮箱后的结构性能，提出了对浮箱结构的四个整改方案，并利用Fuzzy综合评判理论对其浮箱拼装优化进行综合评判，具有一定的应用价值。

拼装式起重船；结构强度；浮箱；有限元；Fuzzy综合评判理论

0 引言

为保障物资输送和维持海上的交通通畅，浮箱技术的研究和运用将作为首选。浮箱作为重要的浮渡工具，不仅能在战时用于跨越江河或海滩障碍，同时也在平时的抗洪抢险、桥梁施工和船舶航行作业等国民经济建设中发挥重要作用，其重要性越来越受到国内外企业的重视。而起重船作为海洋工程的辅助船舶，不仅在海洋油气田的开发过程中发挥着重要的作用，还是海上工程吊装、海洋打捞作业中不可或缺的装备。该种类型的船舶近年来得到了大力的发展。[1，2]因此，本文主要工作是将浮箱增设到起重船后，计算自身的结构强度和研究浮箱的拼装性能。

1 110t拼装式起重船有限元分析

1.1 有限元模型

按照《船舶与海上设施起重规范》（2007）（以下简称“规范”）进行建模与边界处理，同时利用有限元软件MSC/PATRAN及MSC/NASTRAN对110t拼装式起重船船体结构强度进行有限元校核计算。在建模过程中，沿着船长方向定义为X方向，沿着船宽度方向取为Y方向，高度方向就看作Z方向。[3]船体有限元模型共有7 544个节点，9 204个单元；浮箱有限元模型共有2 568个节点，2 514个板单元，有限元模型如图1所示。

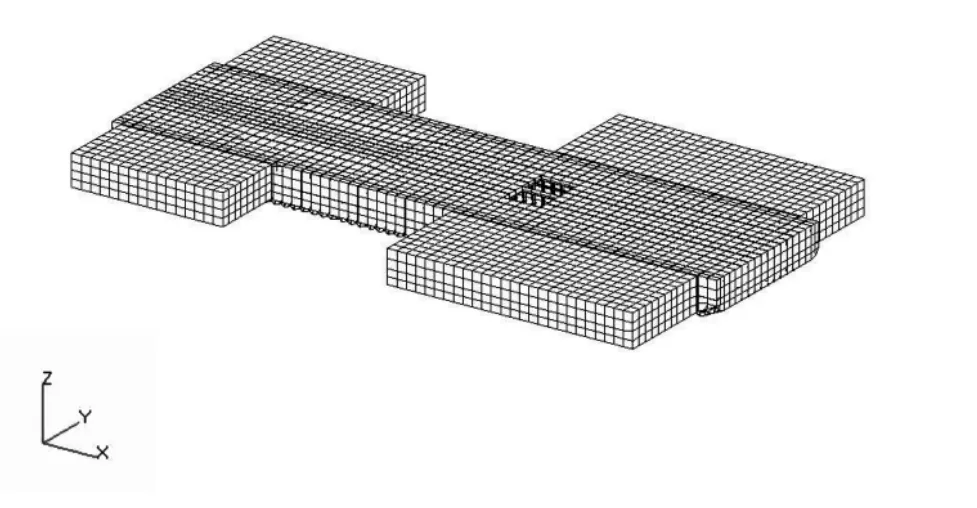
图1 整体有限元模型

1.2 边界条件与载荷加载

在对110t拼装式起重船整船有限元分析时，需要对模型边界进行确定，结合规范的要求，边界条件如表1所示。

表1 110t拼装式起重船整体的边界约束

本船的计算荷载工况主要考虑到有风无风、吊臂位置等因素。在计算过程中往往涉及到危险工况来分析，所以本文的工况可包括6种，具体是：工况1，扒杆起吊角度为70°，此时不考虑风载；工况2，扒杆处于过桥的时候，起吊角度为12°，同样不受风载；工况3，扒杆起吊角度为70°，此时考虑风载；工况4，组合受载，风速55m/s（前后方），静横倾30°，甲板前后上方受到加速度影响；工况5，组合受载，风速55m/s（横向），静横倾30°，甲板前后上方受到加速度影响；工况6，扒杆起吊角度为70°，同时受到组合载荷影响。

加载位置：根据总布置图以及载荷计算所得值，加载位置为扒杆底部与甲板接触位置。在对整船有限元分析时，必须要采取MPC对主船体以及浮箱之间关系，这样可以更好地传递他们之间的载荷，如图2和图3所示。

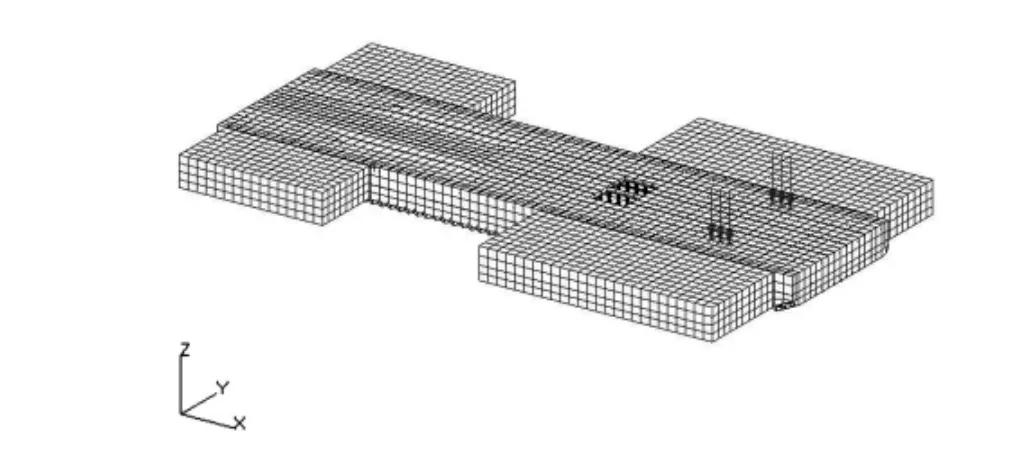
图2 船体整体载荷加载

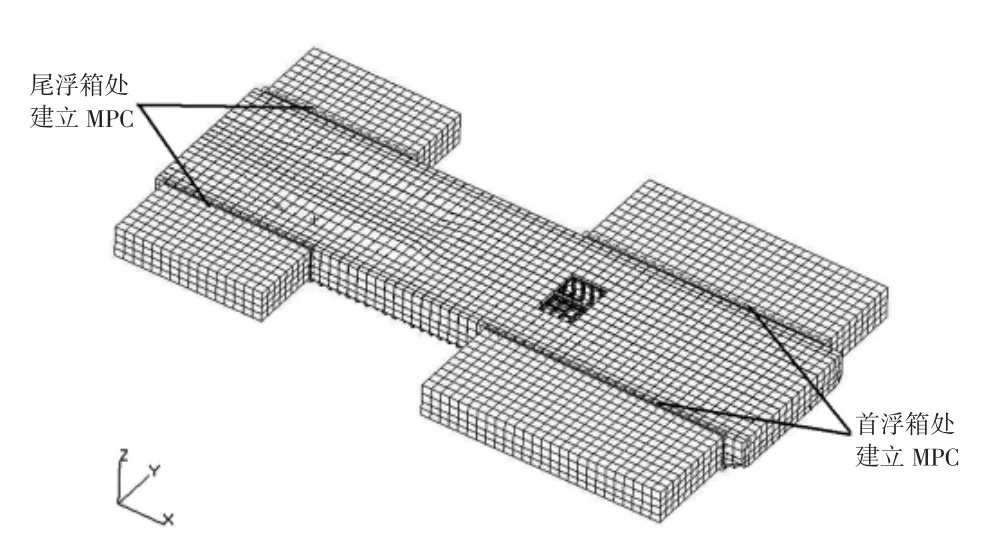
图3 采取MPC建立主船体与浮箱连接图

1.3 许用应力

按照规范的规定，确定出不同工况下的起重机结构安全系数以及许用应力，船体构件许用应力如表2所示。

表2 船体构件许用应力

1.4 应力结果

通过对110t拼装式起重船船体结构的计算，应力结果如表3所示，并有以下结论：

（1）该船在6个工况下的有限元强度均满足规范许用应力的要求；

（2）船体在工况6，即扒杆起吊角度为70°，同时受到组合载荷影响下计算出来的应力最大值为132MPa，其原因主要是船舶受到组合载荷影响，不仅有风速还有加速度等因素，造成船舶应力较大。

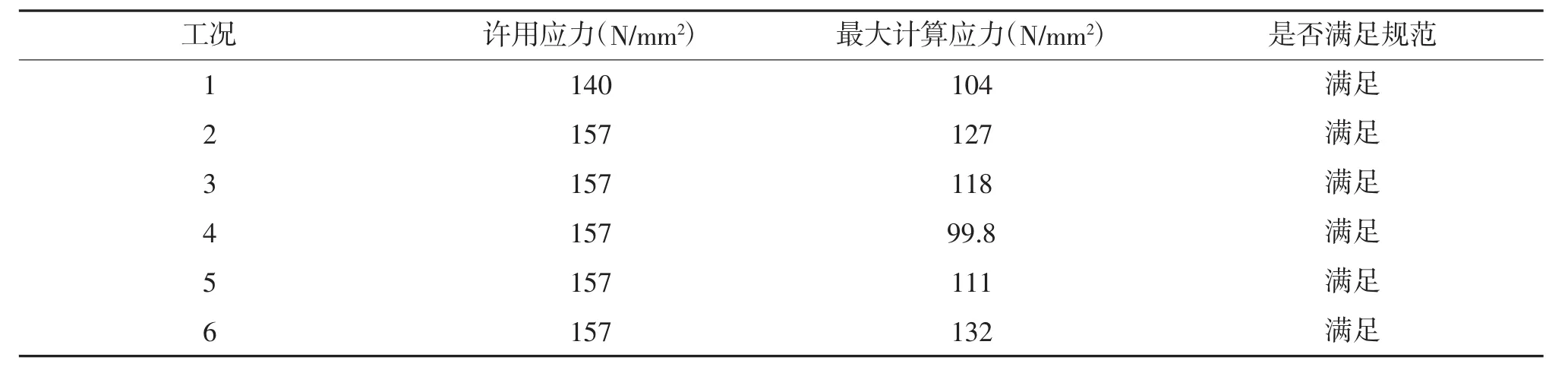
表3 应力水平汇总

2 浮箱体结构性能研究

2.1 概述

基于对110t拼装式起重船结构强度的研究，可提出如下四种浮箱改进方案，研究对船舶整体强度的影响。具体为：方案Ⅰ，在尾浮箱内部增设横舱壁；方案Ⅱ，在尾浮箱内部增设纵舱壁；方案Ⅲ，增加尾浮箱与靠近船体舷侧外板的厚度（从原来的6mm增加为7mm）；方案Ⅳ，把首尾浮箱做成一个整体，不改变其高度。

2.2 计算结果比较

改进后的浮箱结构在起重船受到外载荷作用下，拼装式起重船应力计算结果比较如表4所示。可以发现，不同方案之下的110t拼装式起重船的船体强度应力都有所提高，这为今后拼装式起重船结构的设计提供一定借鉴意义。

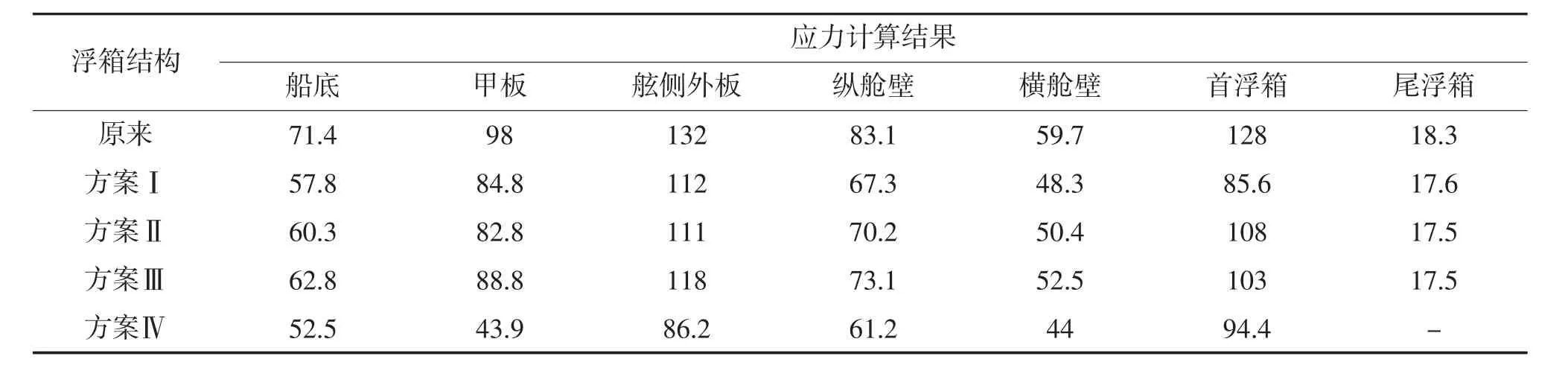
表4 应力比较（MPa）

3 拼装式起重船结构的模糊综合批判

下面将主要通过Fuzzy综合评判理论对前面提到的四种方案进行综合评判，确定最优方案，这样也会为实际建造提供一定参考意见。

3.1 建立评判对象因素集

评判对象因素集如式（1）所示。式中，u1为安全性；u2为工艺性；u3为经济性。其中u2（工艺性）由切割长度的数值、加工场所的具体情况、装配情况、涂装技术要求等四个子因素确定，如式（2）所示。式中，u21为切割长度；u22为加工条件；u23为装配条件；u24为涂装。

3.2 建立因素权重集

在建立因数权重集时，首先需要对安全性、工艺性和经济型进行整体确定权重，在此可以认为第一层因素权重模糊集。从这三个因素中，安全性最重要，直接影响船舶在码头装载和航行过程中船舶以及人员的安全，而工艺性是在安全性得到满足的前提下，对船舶切割、加工、装配等技术指标的改进与提高，经济性因素的重要性相对最小，仅仅出于船舶营运为目的而考虑的一项因素，通过表5可得权重A=（0.366，0.337，0.297）。在建立因数权重集时，还需要对工艺性中涉及到切割长度的数值、加工场所的具体情况、装配情况、涂装技术进行确定权重，在此可以认为第二层因素权重模糊集。在本文选定的四项指标中，钢料切割最重要，对船体建造工艺的质量起到很大影响，也影响了此结构的强度，因此该项指标最重要。构件加工和装配在切割的基础上进行的，也比较重要，直接影响焊接的工作量以及分段建造工艺要求，涂装的重要性相对最小，通过表6可得权重A2=（0.283，0.269，0.242，0.206）。第一层进行的自上而下的成对比较，具体数值如表5所示。第二层进行的自上而下的成对比较，具体数值如表6所示。

表5 第一层因素权重模糊集

表6 第二层因素权重模糊集

3.3 建立评判集

从这四种方案中选取一种最优方案作为最终优化方案，所以评判集可以简单表示，如式（3）所示。

式中，V1为方案Ⅰ；V2为方案Ⅱ；V3为方案Ⅲ；V4为方案Ⅳ。

3.4 评估指标的量化

在评估以下三个指标中，对构件加工、装配以及涂装的要求可以跟实际建造拼装式起重船的船厂相结合，认为方案Ⅲ不管从加工、装配还是涂装都比较简单，而方案Ⅰ和Ⅱ通需要增设舱壁结构，增加加工装配等焊接工作量，相对复杂一点，方案Ⅳ从首尾浮箱整合角度出发认为建造工艺要求最高，而涂装技术跟方案Ⅲ没有太大变化。因此，可得到模糊权重集如表7所示。

表7 评估指标量化

通过参阅相关资料可以总结出相关统计函数。以实际数值、最大允许值和相关统计公式的方式，分别对其余三项指标给予简单数值化，具体如表8所示。

表8 三项评判指标

3.5 第二层因素权重模糊集

拼装式起重船的船体安全性、工艺性、经济性的指标如表9所示。

表9 安全性、工艺性、经济性的指标

将表9中设计到u1，u21，u3的具体的数据放到表8所要求的各种统计公式函数中，这样可以得到不同指标下的数值。结合前面表7的计算结果，得到安全性、工艺性（切割长度）以及经济性参数的评判模糊集。最后得到第二层因素权重模糊集，如式（4）所示。

3.6 第一层因素权重模糊集

同理可以得到第一层因素权重模糊集，如式（5）所示。

通过Fuzzy综合评判理论计算，得到了最终因素权重模糊集B，其中方案Ⅳ的值最大，说明方案Ⅳ对拼装式起重船整体的性能最为理想。

4 结束语

本文主要基于110t起重船的基础上，在两侧增设首尾浮箱后研究整体的结构性能。同时针对起重船发展现状和工程背景，对110t拼装式起重船的结构性能进行深入的研究分析。通过对拼装式起重船浮箱的研究，可以得出比较优良的浮箱结构。这种结构不仅加强了起重船本身的强度，也提高了船舶的稳性和抗沉性，进而也为起重船进行高难度施工作业提供有力保障。

[1]王淑平,王波.3000t海上运架梁专用起重船结构设计[J].船舶设计通讯,2006(2)：48-51.

[2]张志明,徐丹铮,张超,等.大型起重船船型开发的若干技术问题初探[J].船舶,2005(1)：10-15.

[3]张永昌.MSC NASTRAN有限元分析理论基础与应用[M].北京:科学出版社,2004.

Research on the Structural Strength of the 110t Assembled Floating Crane as well as the Assembling Optimization of the Floating Box

LI Ai-hua
(School of Ship,Oceanic&Architectural Engineering,Shanghai Jiaotong University,Shanghai 200240,China)

Based on a study of the structure performance of the floating boxes installed on both flanks of a certain 110t assembled floating crane,this article puts forward four rectification measures as well as makes a comprehensive evaluation of its assembling optimization in combination with the FUZZY theory.

Assembled floating crane;Structural strength;Floating box;Finite element;FUZZY theory

U674.35

A

1671-9891（2014）03-0030-05

10.3969/j.issn.1671—9891.2014.03.009

2014-04-25

李爱华（1968—），男，江苏如东人，上海交通大学船舶海洋与建筑工程学院硕士生。