飞机柔性件铆装中的接触力建模与偏差分析
2014-04-13谭昌柏王志国
张 雪,谭昌柏,王志国,周 强
(南京航空航天大学机电学院,江苏南京 210016)
飞机柔性件装配的主要方法是铆接装配,铆接通常会引起较大的装配变形,且由于影响因素众多而难以分析控制,装配工艺过程严重影响飞机制造的质量。从质量工程的角度对柔性件铆接装配偏差进行合理预测和分析,对于减少飞机制造中的尺寸协调问题、提高飞机制造准确度具有重要意义。
在柔性件装配分析模型研究中,大多采用有限元模型分析和仿真装配过程,Liu和Hu[1]将影响系数法与统计分析方法相结合,基于柔性件线弹性假设,利用有限元分析方法分别提取零件和装配体的刚度矩阵,推导和建立了装配偏差和零件输入偏差之间的线性关系,克服了直接采用有限元法建模时计算工作量大、效率低的缺点。但该方法在建立敏感度矩阵时,没有考虑接触作用对装配过程的影响,在某些装配过程中,零件存在较大的干涉接触作用,此类接触对于最终的装配偏差存在较大影响。因此,上述装配偏差分析模型在准确度和可靠性方面存在一定局限性。Dahlström 和 Lindkvist[2]针对装配过程中影响系数法未考虑接触作用的问题,提出了基于影响系数法的接触力模型。该模型研究了接触力对装配力和回弹变形的影响,其局限性是仅考虑装配力沿夹紧方向大小相同情况下的平衡焊枪装配情况。飞机铆接装配的受力特点具有不同于平衡焊枪装配的特点,通常需要将零件压紧到理论连接位置进行铆接,上述方法没有关注接触状态下如何保证连接点位于指定位置的问题,且没有研究定位夹紧力和铆接力大小的求取方法,只是通过多次试验来确定。Kang Xie[3]等人研究了柔性件装配过程中考虑接触的尺寸偏差累积模型,提出了修正维数缩减法(Enhanced Dimension Reduction Method),基于 ABAQUS的参数化建模方法,采用有限元分析实现了二维零件的尺寸接触模型,但该模型仅应用于二维模型,未能实现三维有限元模型的接触力建模。本文基于测量数据的三维零件模型,对接触力模型在装配仿真过程中的实现、装配偏差分析等问题进行研究。
1 柔性件铆接装配过程建模
目前,关于柔性件装配偏差分析的相关研究中,最具代表性的是基于装配过程柔性件线弹性变形假设的影响系数法[4](Method of Influence Coefficient,MIC)。其基本思想是通过力学模型建立柔性件局部受力与变形的线性关系,然后运用该模型进行装配偏差统计分析,该方法的显著优点是在效率上远远优于直接运用有限元分析工具建立仿真模型进行偏差分析的蒙特卡罗仿真法[1]。
关于柔性件装配过程的偏差来源,影响装配准确度的主要因素包括以下几方面:偏差(零件偏差、过程偏差)、装配方案(装配顺序、夹具方案、连接配置)和概念设计(几何体形状、刚度条件、零件数量、接头类型)[5]。
1.1 基于线弹性假设的装配偏差分析
线弹性假设方法是基于柔性件小变形、线弹性的假设,运用线性有限元的方法研究柔性件在装配过程中装配力与装配变形之间的关系,建立反映装配前后柔性件关键测点偏差之间关系的力学模型。
飞机柔性件装配的过程中,由于零件制造偏差、装配夹具偏差以及定位偏差的耦合,相互具有连接关系的零件在装配点会形成一定的位置偏差。为了完成装配,需施加一定的装配力,强制柔性件变形,使装配点的偏差闭合。零件变形可以分为弹性变形和塑性变形,弹性变形是线性的,塑性变形是非线性的。小变形情况下,可认为零件只有弹性变形,这时位移与受力的关系是线性的。柔性件在装配过程中的变形是小变形,可以假设为线弹性的过程,刚度矩阵K不变。在这种假设的前提下,可以运用线性关系式表达力F与变形量δ之间的关系,如式(1)所示。

有限元模型的总体刚度矩阵是大规模的稀疏矩阵,不利于计算。本文根据线性分析各阶段的柔性件定位以及约束加载边界条件,利用商业软件ANSYS提取超元刚度矩阵,超元刚度矩阵只包含对装配偏差起作用的关键节点及自由度,大大简化了矩阵,提高了计算效率。
1.2 柔性件铆接装配过程分解
飞机柔性件铆接,首先采用夹具对工件进行定位夹持,然后用铆枪(铆机)将两柔性件上的铆接点定位到理论连接位置并铆接,随后释放铆枪(铆机),两板回弹至平衡位置。根据装配中不同的力作用过程可将柔性件的铆接过程分为以下4个步骤。
步骤1:零件定位,即参与装配的零件各自定位在夹具上,如图1(a)所示。零件存在制造误差,图中零件在关键点处的制造偏差分别为V1和V2。
步骤2:铆枪把薄板零件夹持到名义位置,如图1(b)所示。铆枪对两个薄板分别施加铆接力F1和 F2,则有
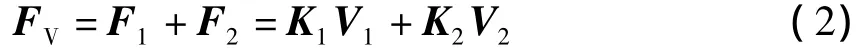
式中:FV为施加到两个零件上的装配力;K1和K2分别为两零件的刚度矩阵。
步骤3:铆接两薄板零件,如图1(c)所示。两柔性件通过铆接的方式连接在一起。连接后装配体的总刚度矩阵变为KZ。
步骤4:释放铆枪及部分夹具,装配体从名义位置回弹至平衡位置,如图1(d)所示。于是,回弹力FH与回弹位移U之间有以下关系:FH=KZU。回弹力大小应等于两板的定位夹紧力和铆接力,即

因此有

式中:S1和S2为装配体偏差相对于两零件铆接点偏差的敏感度矩阵;S=[S1,S2];V=[V1,V2]T。

图1 柔性件铆接过程示意
按照以上对装配过程的分析,可建立装配误差与零件输入误差之间的线性关系,通过预测装配体的质量来评价零件制造误差和设计方案是否符合制造准确度要求,提高了仿真分析效率。
2 基于线弹性假设的接触计算分析
铆接装配中的接触问题属于边界非线性问题。由于基于线弹性假设的柔性件装配过程建模难以将接触力影响直接纳入力与位移的简单线性关系中,相关研究也很少考虑装配中柔性件的相互接触问题,然而在装配存在较大零件干涉的情况下,薄板件可能出现相互穿透这种与实际装配情况相悖的情况,严重影响分析结果的准确性和可靠性。
铆接装配工艺通常要求连接件在指定连接位置下形状闭合,即需求解给定铆接位置条件下的装配力。铆接完成后,进行接触计算,将参与装配的两个柔性件分为上侧面和下侧面,并规定上侧面的节点不可穿透下侧面的单元,以约束两柔性件的干涉行为。接触计算主要解决装配中接触状态分析、接触力与节点位移关系、接触平衡计算等问题。
基于接触的装配偏差分析流程如图2所示。

图2 基于接触的装配偏差分析流程
2.1 装配中动态接触状态分析
基于三角网格模型进行几何干涉分析,通过计算网格模型中上侧板节点与下侧板单元的距离矢量,判断上侧板节点干涉情况及干涉量。
如图3所示,已知上侧面节点P在笛卡尔直角坐标系中的坐标,下侧面相应的最近的单元ΔABC的法矢n,节点A,B,C的坐标,那么可知上侧面节点与相应下侧面单元的距离d=AP·n,其中AP为以A为起点、P为终点的向量。
当d>0时,节点P处于ΔABC的法矢正方向一侧,未发生干涉;
当d=0时,节点P处于ΔABC面内,未发生干涉;
当d<0时,节点P处于ΔABC的法矢负方向一侧,发生干涉。

图3 零件接触状态分析示意图
2.2 节点间接触力的等效转化
上侧面节点与相应下侧面单元的相互作用力应满足力与力矩平衡条件。如图4所示,P'为上侧面节点P在下侧面单元ΔABC的投影点,分别以ΔABC三条边为转矩,按力与力矩平衡条件分别求出ΔABC的各节点所受的接触反力。设P点受单元ΔABC作用力为R,ΔABC顶点A,B,C受到的反作用力为 RA,RB,RC,满足条件:

式中:SA为ΔP'BC的面积;SB为ΔP'AC的面积;SC为ΔP'AB的面积。

图4 接触反力求解示意图
2.3 节点干涉量与接触力的线性作用关系
发生接触的两个物体必须满足3个条件[6-8],即:(1)单边接触条件,两薄板之间间隙必须大于等于零,即d≥0;(2)压力条件,两薄板之间相互作用力必须为负,即为正压力,p≤0;(3)补充条件,受压力的节点,与对应单元处于恰好接触状态,即p×d=0。
为了消除已经产生的干涉,在干涉节点上施加接触力,使之回到正常位置,那么选择节点的次序、施加接触力的大小以及判定接触状态正常与否的条件将是接触算法的重点。
在小变形的装配过程中,零件的几何形状、夹具布局、零件的节点和单元间的相互位置关系近似不变,为简化接触问题建模和提高效率,不妨认为接触位置迭代过程中节点受力与节点间隙的作用关系保持不变。
若上侧面可能发生接触的区域共n个节点,设任意节点i受到接触力Ri作用,该区域受到接触力 RUp(RUp={R1,R2,…,Rn})作用,相应的下侧面接触区域单元中各节点受到等效接触力RDown作用,则RDown与RUp满足力与力矩平衡条件。在两柔性件夹紧、铆枪压紧以后,两薄板在接触区域发生干涉,设第j个节点与相应下侧面单元的初始间隙为d0j,在该节点上施加单位力,相应下侧面单元也将产生力的响应,从而引起上侧面n个节点与相应单元的间隙发生变化,这些距离变化相应可以用向量{c1j,c2j,…,cnj}T表示。
在第j个节点上施加非单位力Rj时,则有n个间隙变化响应为{c1j,c2j,…,cnj}TRj。
在接触区域各节点上施加力R={R1,R2,…,Rn},由接触区域节点与相应单元的间隙改变量组成的矩阵为:

式(6)中接触力向量R和最终的间隙向量d未知。经过接触计算的最终结果必须满足接触的上述3个条件:任意dj≥0;任意Rj≤0;所有满足Rj≠0 的节点,dj=0(j=1,2,…,n)。
3 接触平衡位置的迭代算法
接触平衡算法以接触区域节点干涉量与接触力的线性关系为依据,以单边接触条件、压力条件和补充条件为约束,通过动态地调整各节点的接触力和节点位置,多次迭代求解后得到零件平衡位置,平衡后的零件间接触力也是后续回弹力计算的基础。
应用接触算法解决干涉问题的基本思路是通过对接触区域存在最大干涉量的节点施加接触力来消除干涉,同时更新网格节点位置,再按照接触的条件进行检测,若仍存在干涉则重复上述过程,通过多次迭代求解接触力和接触平衡位置。接触算法流程如图5所示。初始阶段,接触力向量R清零(即两板不存在接触力)。首先,寻找上侧面接触区域中发生干涉最严重的节点i,即最大穿透点,dmin=di。在该节点施加绝对值尽量小的接触力Ri,其大小刚好使接触区域某一节点的干涉消除。Ri被记录和累加于接触力向量R中。根据式(6)更新两板之间的间隙向量d。检验上侧面所有存在接触力的节点,是否间隙为非正(条件3)。如果条件不成立,则记录下不满足条件的节点号m,并在i点和m点分别施加一定的接触力改变量ΔR(与R的正负相反)。为了避免接触力向量中出现拉力,必须检验所有接触力是否均为非正值(条件2)。如果不成立,则需要将不满足条件的节点间接触力设置为零。然后重新计算间隙向量,直至满足条件2和3。最后,检验间隙向量d是否全部为非负(条件1),假如满足条件,则算法结束,否则回到第一步寻找发生干涉最严重的节点,重新循环。

图5 接触算法流程图
以上算法仅适用于铆接力和穿透较小的情况,这是因为只有在小变形情况下,线性响应假设才能成立,式(6)才可用。存在较大装配变形和干涉的情况下,上述算法依据的线性响应方法可能导致算法的不可靠或难以收敛。解决方法是将铆接装配过程分为若干小变形阶段,然后采用部分析因设计方法来建立不同阶段的节点作用力和间隙的线性关系,这种分段线性逼近的方法可以更好地体现接触的动态非线性特点。
4 实验验证
为了验证本文提出的接触力建模方法,采用Visual C++6.0和OpenGL技术实现了上述接触力建模和装配偏差分析算法,并在柔性件装配实验台上进行了装配偏差分析实验。一方面,通过软件分别在考虑接触和不考虑接触两种情况下进行柔性件装配仿真,记录关键节点的位置信息。另一方面,在实验平台上进行装配实验,测量并记录零件上关键点位置信息,如图6所示。该装配实验台固定两薄板一端,铆接区域两侧采用过约束的夹头压紧,在两板重叠区域进行铆接。

图6 柔性件装配偏差实验
零件制造误差、夹具定位误差引起装配体在装配耦合位置的偏差,该偏差在夹具和铆枪的作用下被消除。夹具和铆枪释放后,装配件在回弹力的作用下到达最终平衡位置。
图7所示为根据该装配过程建立的有限元网格模型及其约束,两个柔性件采用相同的定位方式,分别有两个固定点(用▲标示),限制 x,y,z向自由度;3个定位夹紧点(用△标记),限制z向自由度;两个铆接点(用●标记),限制6个方向自由度。定位夹紧点在回弹阶段被释放。

图7 装配偏差的有限元仿真分析模型
两柔性件的材料属性为:弹性模量 E=72GPa,泊松比v=0.3。采用shell63三角形单元(ANSYS单元类型)。两薄板尺寸均为340mm×300mm×0.85mm,各包含158个单元和87个节点。采用vmax/L=3.7/340的实验情况。
在考虑接触和不考虑接触情况下分别进行薄板装配仿真,两柔性件装配回弹后的状态如图8所示。可见,在不考虑接触情况下,零件间发生了明显的穿透现象。

图8 考虑接触与不考虑接触的装配仿真
对比装配仿真与装配实验回弹后的节点位置信息,结果见表1。由表中可知,采用仿真分析时,考虑接触情况下节点位置相对于实验结果的平均偏差为-0.176%,而不考虑接触情况下的节点偏差相对于实验结果的平均偏差为-6.711%。由此可见,考虑接触时装配偏差分析结果比不考虑接触的装配偏差分析更接近实际的装配结果,接触现象对于装配仿真过程的精确度有很大影响。

表1 装配偏差实验结果与仿真结果对比
6 结束语
本文提出的飞机柔性件铆接中的接触力建模和装配偏差分析方法,着重解决基于几何干涉分析的接触状态检测、接触平衡求解算法,使得仿真过程更加接近真实装配过程。但是目前的研究仅通过较为简单的柔性平板件验证了飞机柔性件装配接触力模型,要提高该模型的适用性,还需要采用更加复杂的飞机曲面零件为研究对象,拓展接触力模型的应用范围。
[1] Liu SC,Hu SJ.Variation simulation for deformation sheet mental assemblies using finite element methods[J].ASME Journal of Manufacturing Science and Engineering,1997,119:368-374.
[2] Dahlström S,Lindkvist L.Contact modeling method of influence coefficient for variation simulation of sheet mental assemblies[C]//2004 ASME International Mechanical Engineering Congress and Exposition,Anaheim,California USA,2004,11:13-20.
[3] Xie K,Wells L,Jaime A,et al.Variation propagation analysis on compliant assemblies considering contact Interaction[J].ASME,2007,129:934-942.
[4] Liu SC,Hu S J,Woo T C.Tolerance analysis for sheet metal assemblies[J].Journal of Mechanical Design,1996,118:62-67.
[5] 邢彦锋.基于柔性偏差分析的车身装配顺序优化研究[D].上海:上海交通大学,2008.
[6] Hills D A.Mechanics of Elastic Contacts[M].Oxford:Butterworths,1993:115-116.
[7] Mijar A R,Arora JS.Review of formulations for elastostatic frictional contact problems[J].Structural and Multidisciplinary Optimization,2000(20):167-189.
[8] Stavroulaki M E,Stavroulakis G E.Unilateral contact application using FEA software[J].International Journal of Computer Mathematics,2002,12(1):115-125.
