基于响应曲面法的表面粗糙度预测模型研究

亓 剑，阎 兵

(天津职业技术师范大学机械工程学院，天津 300222)

基于响应曲面法的表面粗糙度预测模型研究

亓 剑，阎 兵

(天津职业技术师范大学机械工程学院，天津 300222)

通过正交试验，研究了高速端铣加工中切削参数对表面粗糙度的影响。采用田口设计方法和响应曲面法构建了表面粗糙度预测模型，分析了主轴转速、进给量、切深对表面粗糙度的影响。结果显示，进给量对表面粗糙度的影响最显著，主轴转速次之，切深的影响不大。模型预测精度为99.84%，达到了较高的预测水平。

高速加工;端铣;表面粗糙度;响应曲面法;试验设计;田口设计

在数控加工中，多种因素会对最后成形工件的质量和制造业的经济成本产生直接影响。刀具的材料、机床控制系统、不同类型的刀具夹持器、机床的轴向性能和切削参数(主轴转速、切深、进给量和步距)都是直接影响成形工件表面质量的重要因素。而在加工过程中，尤其是在产品生产周期最后阶段，表面粗糙度是表征表面光洁度、尺寸和几何性质的重要指标，是决定产品质量的重要参数［1］。目前预测表面粗糙度的方法主要有建立回归方程、表面形貌分析、构建神经网络［2］等。神经网络具有并行处理自学习以及特有的非线性适应性信息处理能力的优点［3］，适用于处理需要同时考虑多种因素和条件的模糊信息处理的问题，但需要大量的数据进行训练。文献［2］采用了自适应神经模糊推理系统，通过进行大量试验，建立了粗糙度预测模型。本文综合田口设计和响应曲面法，用较少的试验数据获得粗糙度预测模型。

1 基于田口方法的试验设计

田口设计是由日本田口玄一博士创立的一种聚焦于最小化过程变异，或使产品、过程对环境变异最不敏感的实验设计方法，能够设计出环境多变条件下优化、稳定的试验方案。田口设计通常采用正交表来设计试验，用较少的试验次数来获取更多的信息。

在机械加工中，切削用量的选择是否合理，直接关系到生产效率、加工成本、加工精度和表面质量，以外圆纵车为例，单件机动工时为:

在特定工序中，A0为常数，S为切削速度，D为切深，F 为进给量［4］。由式(1)可以看出，S，D，F 的乘积对生产效率有着直接影响，但它们之间又是相互联系、相互制约的，必须采用切削速度、进给量和切深的最佳组合才能得到较高的表面质量。

在研究高速端铣过程中，主轴转速与切削速度有直接关系，选取主轴转速S、进给量F和切深D3个参数，设为x1，x2，x3，分4个水平设计正交试验。如图1所示，试验采用立式加工中心(MAKINO S56)，铝钛硅氮涂覆硬质合金刀具，四切削刃立铣刀，刀具直径为 10mm，切削工件为 100mm×80mm×40mm的K340模具钢，洛氏硬度62，材料成分为:碳，1.10%;硅，0.90%;锰，0.40%;铬，8.30%;钼，2.10%;钒，0.50%。采用 SURFCOM－130A粗糙度检测仪对加工后表面质量进行检测，检测参数为轮廓算术平均偏差Ra。引用文献［2］中16组数据，设计L16(43)正交表。L16(43)表示有16行3列，16表示要做16次试验，3表示有3个因素，数字1～4表示取4个水平。加工参数和等级见表1，试验编码及结果见表2。

2 基于响应曲面法的模型建立及结果分析

2.1 模型建立

图1 立式加工中心(MAKINO S56)以及粗糙度检测仪SURFCOM－130A

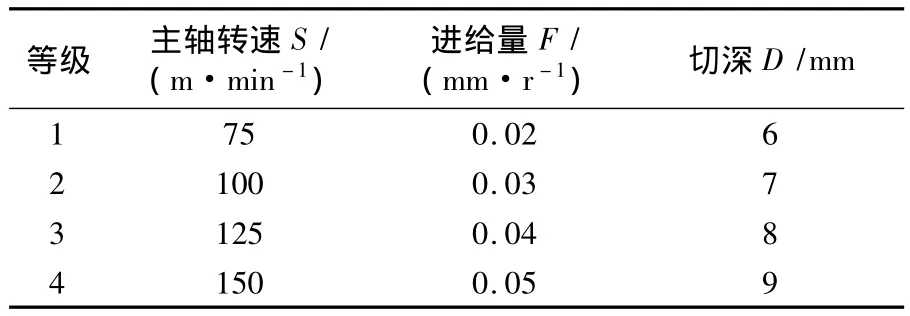
表1 加工参数和等级

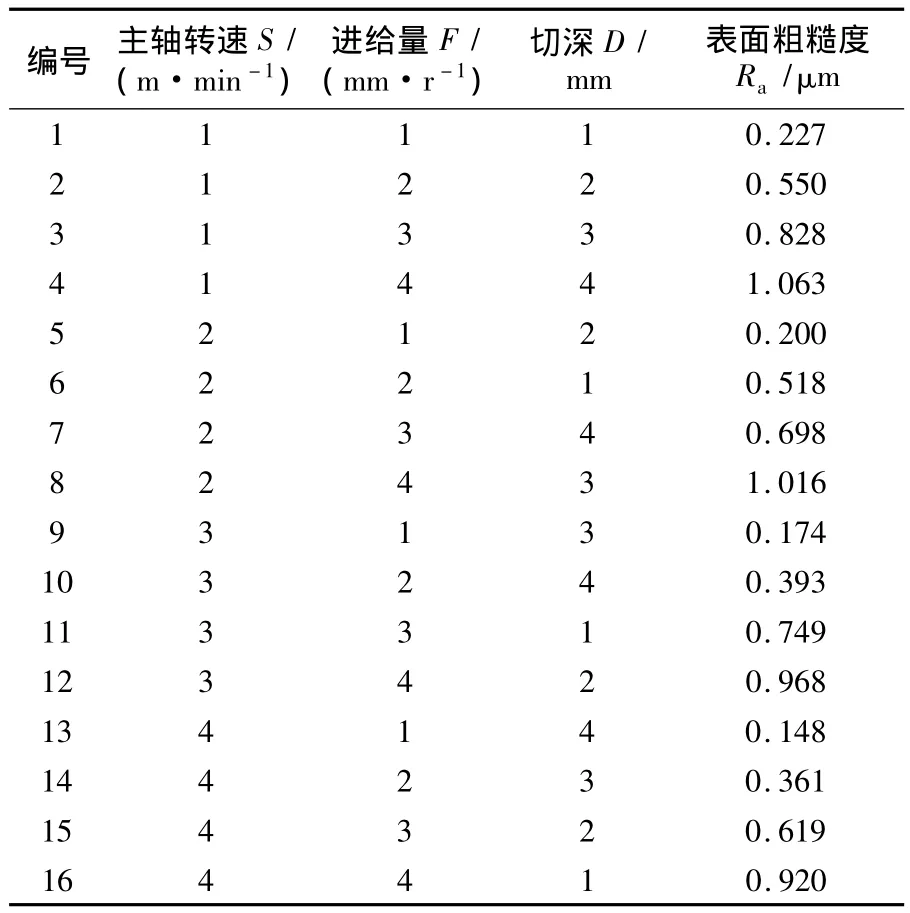
表2 试验编码及结果

D.C.Montgomery提出的响应曲面法(Response surface methodology，RSM)，即非线性回归，是一种结合数学和统计学原理、用于分析多个独立变量如何影响一个独立响应等问题的方法。响应曲面方法采用经验公式模型去逼近输出和输入之间的关系，在工程计算和科学应用中，常常用这种经验模型去表达一些事物的发展规律或描述相关理论［5］。

在本试验中，主轴转速、进给量、切深为独立变量，表面粗糙度为独立响应，为了更准确地了解切削参数对加工表面粗糙度的影响规律，采用二次数学回归的方法建立表面粗糙度和切削参数之间的关系:

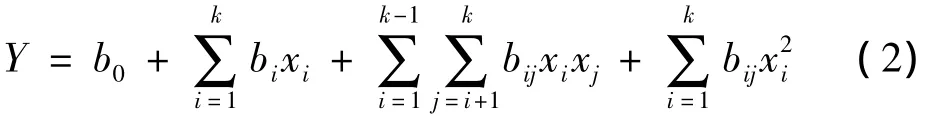
式中:xi为 m维自变量的第 i分量;b0，bi，bij为多项式的待定系数。将待定系数按照一定次序排列，可以构成矢量b，利用n个试验点，采用最小二乘法求解矢量b。

根据文中系统响应输出与输入变量的选择，多项式模型响应曲面可表示为［6］:

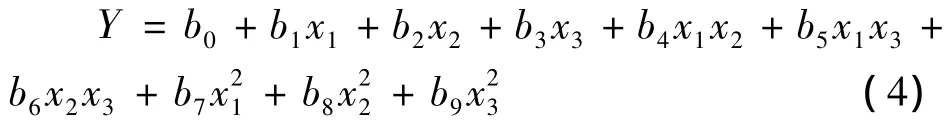
将各试验因素的自由变量和表面粗糙度转换为矩阵，利用最小二乘法，经过拟合，去除无关因子，最终得到表面粗糙度的回归方程:

其中参数 x1，x2，x3的取值范围:x1为 75～150m/min，x2为0.02～0.05mm/r，x3为6～9mm。对回归方程进行方差分析，回归分析计算公式如下:

式中:SS Regression为回归方差;MS Regression为回归均方差;yi为观测值;?为拟合值;为均值;n为试验次数;p为回归方程自由度。计算结果见表3。当检验水平为0.05时，查F分布表知F(6，9)=3.37，远小于计算结果，所以高速端铣平面时，建立的表面粗糙度预测模型的显著性水平极高。另选出16组试验参数进行实际切削，以检验模型的预测精度，结果见表4。

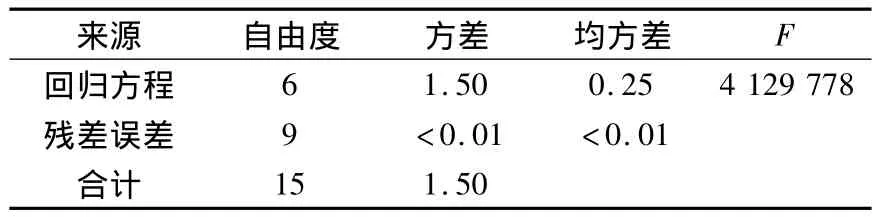
表3 方差分析

从表4可以看出，粗糙度预测误差在1%以内，模型准确度为99.84%，达到了较高的预测水平，说明模型完全可以用来预测工件表面粗糙度。

2.2 结果分析

利用最小二乘法得到主轴转速和粗糙度、进给量和粗糙度、切深和粗糙度的拟合曲线，分别如图2、图3、图4 所示。

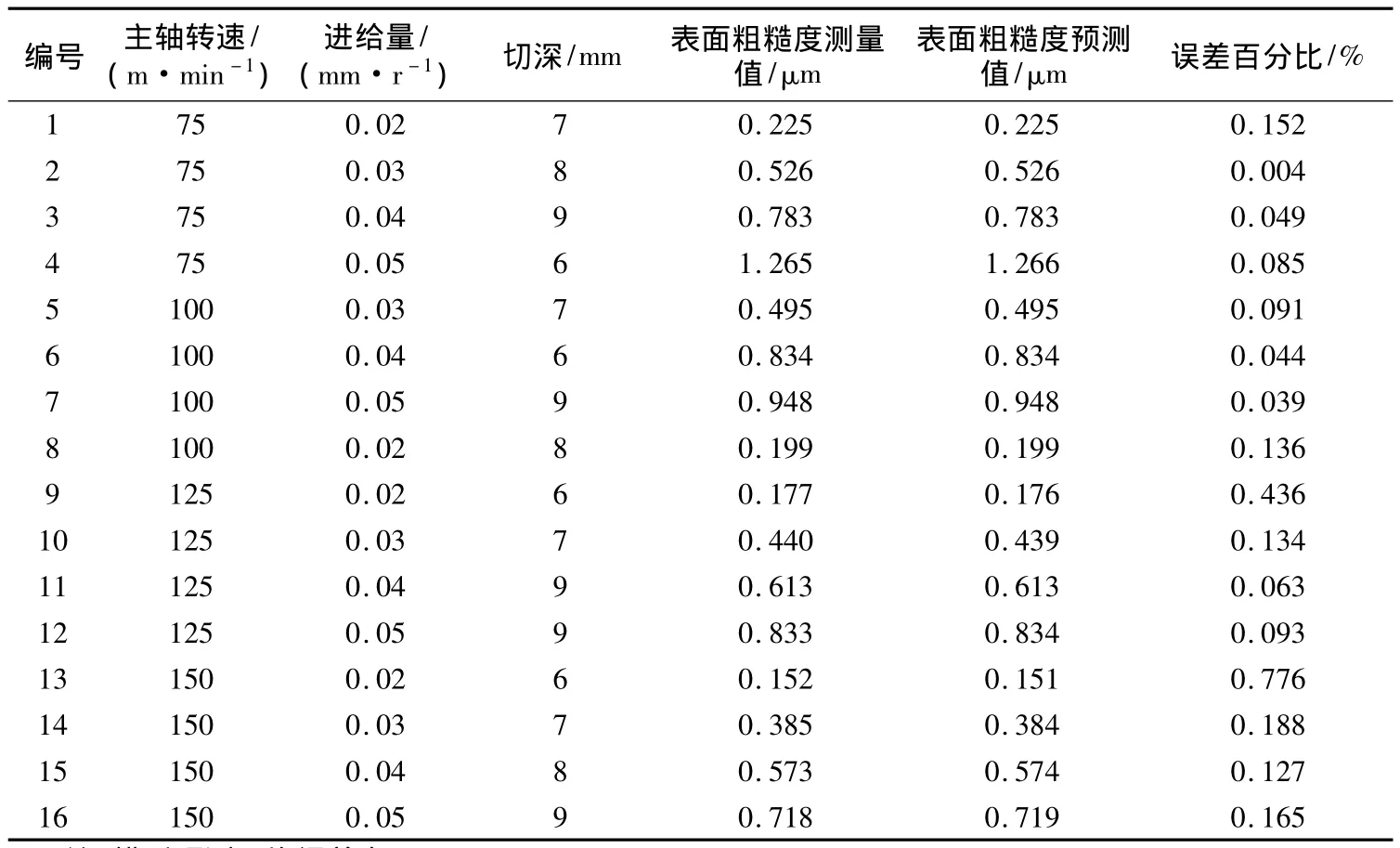
表4 模型验证

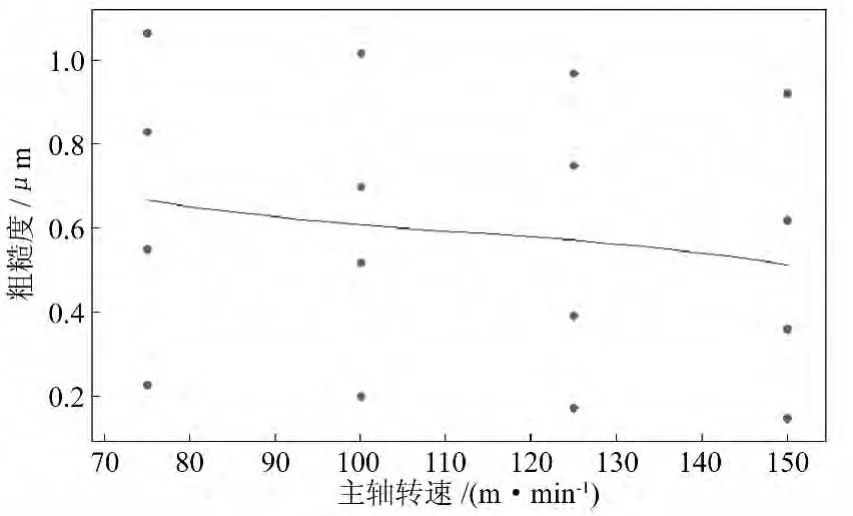
图2 主轴转速与粗糙度拟合曲线

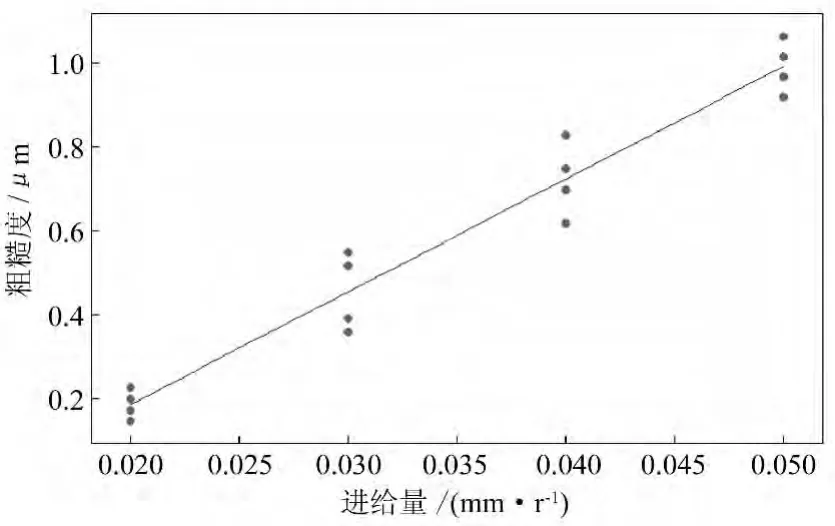
图3 进给量与粗糙度拟合曲线

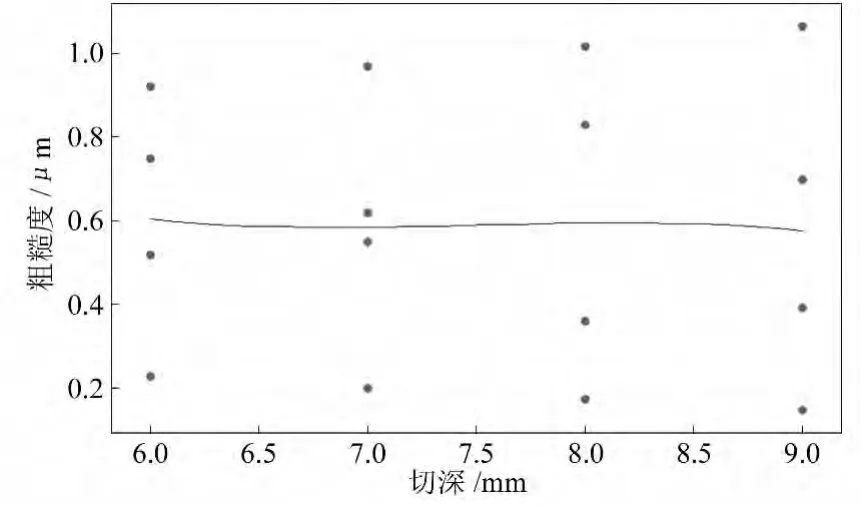
图4 切深与粗糙度拟合曲线

综合回归方程和拟合曲线图可以看出，粗糙度随着进给量的提高而增大，随着主轴转速的增大而减小，而切深对粗糙度的影响不大。进给量对粗糙度的影响最大，主轴转速的影响次之，切深的影响最小。图5、图6、图7分别为粗糙度与进给量、切深，粗糙度与主轴转速、切深，粗糙度与主轴转速、进给量的等值线图。等值线图能形象地反映出试验过程中，粗糙度和任意两个切削加工参数之间的关系。

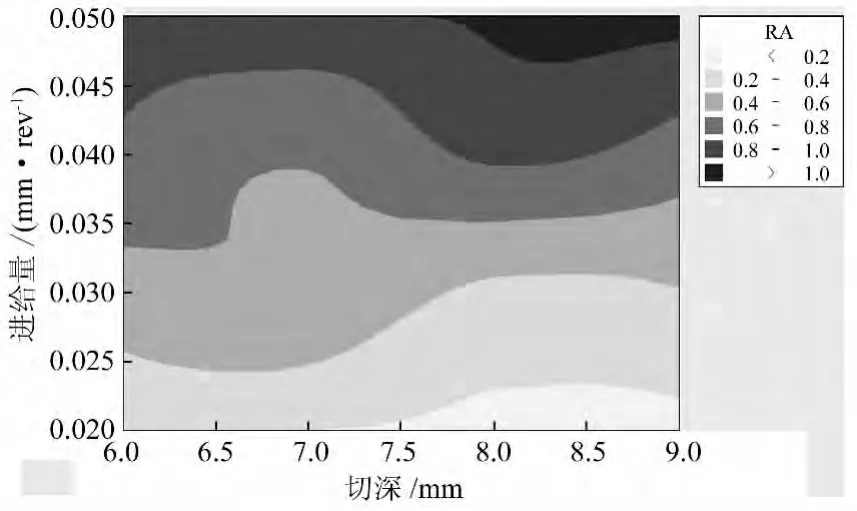
图5 粗糙度与进给量、切深的等值线图

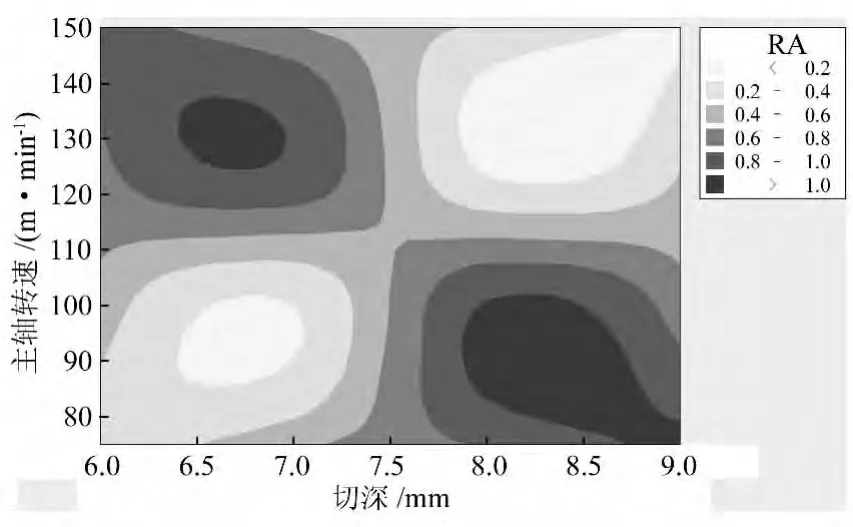
图6 粗糙度与主轴转速、切深的等值线图

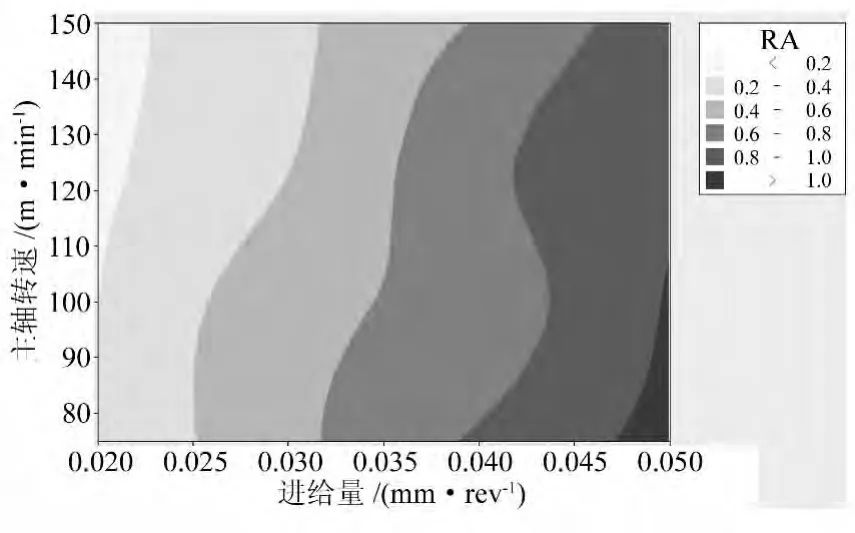
图7 粗糙度与主轴转速、进给量的等值线图

从图5可以看出，当进给量在 0.020～0.035mm/r之间时，随着切深的增加，粗糙度变小;当进给量在0.035～0.050mm/r之间时，随着切深的增大，粗糙度变大。从图6可以看出明显的分段性，在主轴转速为80～110m/min范围时，切深从6.0mm到6.8mm之间粗糙度随着切深的增加而逐渐减小，从6.8mm到9.0mm之间粗糙度随着切深的增加而逐渐增大，并在6.8mm和8.3mm分别达到了粗糙度的极小、极大值;而当主轴转速在110～150m/min范围时，粗糙度和主轴转速、切深的关系恰好相反，在6.8mm和8.3mm分别达到了粗糙度的极大、极小值。而图7再一次验证了进给量对粗糙度的影响较为显著。

3 结束语

本文采用文献［2］中的原始数据，考虑了主轴转速、进给量、切深3方面因素，基于田口设计方法对试验进行了重新设计，并利用响应曲面法构建了表面粗糙度预测模型。影响表面粗糙度的3个因素中，进给量对表面粗糙度的影响最显著，主轴转速次之，切深的影响不大。

相对于文献［2］中的自适应神经网络模型，该模型不需要做大量的试验，同时建立的数学模型有更高的预测精度。结合表面粗糙度预测模型和等值线图，在实际生产中，可结合生产条件，选择最优的切削参数。

［1］ Jayswal S C，Taufik，Mohammad.Modeling and analysis of the surface roughness and geometrical error using taguchi and response surface methodology［J］.International Journal of Engineering Science ＆ Technology，2011，3(7):5809－5817.

［2］ Desale Purushottam S，Jahagirdar，Ramchandra S.Modeling of hardened die steel Böhler K340 for prediction of surface roughness in high speed end milling using adaptive neuro－fuzzy inference system［J］.International Journal of Applied Engineering Research，2012，7(11):1297 －1304.

［3］ 王武，汤三，张元敏.基于神经网络的高速铣削表面粗糙度预报［J］.机械设计与制造，2010(3):216－217.

［4］ 韩荣第.金属切削原理与刀具［M］.哈尔滨:哈尔滨工业大学出版社，2007.

［5］ 刘牧，杨茂奎.基于响应曲面法的表面粗糙度预测模型研究［J］.精密制造与自动化，2006(2):37 －40.

［6］ 张金超，时礼平，余剑，等.基于响应曲面法的表面粗糙度预测模型的建立与切削参数的优选［J］.机械工程师，2012(4):15－17.

Predictive Modeling of Surface Roughness Based on Taguchi Design and Response Surface Methodology

QI Jian，YAN Bing
(Tianjin University of Technology and Education，Tianjin，300222，China)

It presents the effect of process of parameter in high speed face milling operation to predict surface roughness.It establishes the mathematical model to predict surface roughness in terms of machining parameters such as spindle speed，feed rate，and cutting depth.The results show that feed rate is major factor influencing the surface roughness followed by spindle speed and cutting depth，and verifies the mathematical model with confirmatory test and is useful for the prediction of surface roughness.

High Speed Machining;Face Milling;Surface Roughness;RSM;DOE;Cutting Parameters Optimization

TH161+.14

A

2095－509X(2014)01－0073－04

10.3969/j.issn.2095 －509X.2014.01.018

2013－10－16

亓剑(1990—)，男，山东莱芜人，天津职业技术师范大学硕士研究生，主要研究方向为高速、高效、高精加工。