基于免疫遗传算法的铁路列车运行调整研究

李荣娜 张 喜

（北京交通大学交通运输学院 北京100044）

0 引 言

列车运行调整是指在列车运行工作中，因各种因素和突发事件的影响，使得列车运行的实际状态偏离预定值，需要对列车运行方案重新铺划，以尽可能小的代价，尽快地恢复列车的有序运行状态［1］。随着科学技术的进步，国内外有许多学者都注重依托先进的系统来研究列车运行调整问题，以期实现调度指挥的自动化。

目前，学者和专家针对列车运行调整问题提出了数学规划、模拟仿真和人工智能等多种模型与算法。张翠平等根据图论模型的理论建立了列车运行调整问题的线性规划模型，并采用改进的启发式算法进行求解［2］。启发式算法求解速率较快，但对于求解多目标函数时，效果就不太理想。陈雍君以货运铁路为研究对象，建立了以列车旅行平均时间最少为优化目标函数的区间列车冲突调整模型，在求解时使用了序优化方法，减少了计算量［3］。

而在列车运行调整问题中，遗传算法是1种可以很好地模拟列车运行调整过程的算法，一些学者也进行了研究。但是由于遗传算法本身存在的问题，如收敛速度较慢、易出现早熟等，有时候不能获得最优的结果。而免疫遗传算法是将免疫算法与遗传算法相结合产生的1种方法，可在很大程度上避免遗传算法中的早熟现象，从而快速找到全局最优解。

1 列车运行调整的数学模型

选择了双线自动闭塞的线路，并以该调度区段单方向的运行调整问题为例进行研究。为了精确地构造和描述模型，建立以下的相关变量：

M－调度区段内的车站总数；

N－调度区段内列车总数；

Qi，j－列车i在车站j的起车附加时分；

Ti，j－列车i在车站j的停车附加时分；

I－最小追踪列车间隔时间；

Si，j－列车i在车站j的最小作业标准时间；

Dj－车站j可供使用的到发线数量；

列车运行调整的模型建立包括2部分：①目标函数的建立；②约束条件的确定。

1.1 列车运行调整目标函数的建立

列车运行调整的目的就是使偏离列车运行图的列车尽快恢复按图行车。因此，以与列车运行图的偏差最小为优化目标［4］。具体的调整模型如下

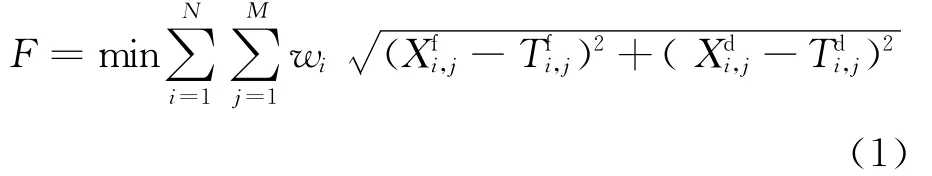
式中：wi为列车i的权重因子，wi越大，说明列车的等级级别越高。

1.2 列车运行调整约束条件的模型化

列车运行调整问题是1个约束条件众多的组合优化问题，所产生的调整计划必须满足一定的约束条件，才可以执行最后求解得到的调整计划。

列车运行调整必须满足的约束条件如下。

1）区间运行时分约束。根据列车在区间的运行时间不得小于区间规定的最小运行时这一规定，有

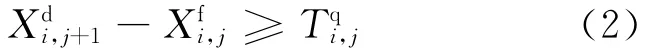
2）追踪间隔时间约束。在区间内追踪运行的2列列车之间需要满足最小追踪间隔时间的约束，即

式中：i为k的后行列车。

3）车站停车时分约束。列车i在车站j的作业时间不得小于规定的在该车站的最小作业时间，该约束条件为

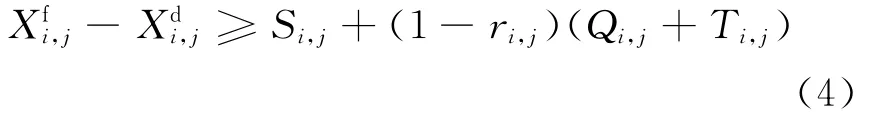
式中：ri，j为列车i在车站j的通过和停站情况，可以定义为

4）发车时间约束。根据发车时间不得早于计划发车时间，有

5）到发线约束条件。由于1个车站可以使用的到发线的数目都是固定的，因此列车实际的到发线使用数目不应该大于车站总的到发线数量。首先，引用一函数，在t时刻，令

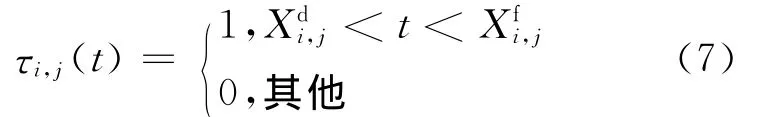
则到发线的约束条件为

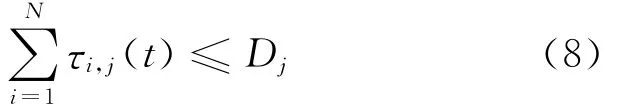
6）越行约束。如果列车在车站发生越行，就需要满足

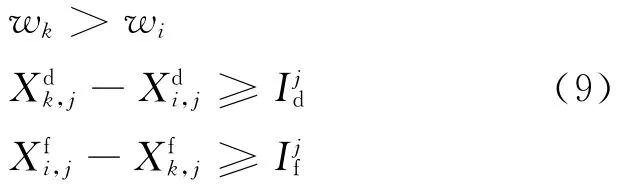
2 基于免疫遗传算法的列车运行调整算法

2.1 算法介绍

遗传算法是以自然界中的生物进化过程为背景，将生物进化过程中的繁殖、选择、交叉、变异和竞争等概念引入算法中［5］。它一般包括以下几个步骤，首先，对问题的解进行编码，并产生编码后的初始种群；根据优化问题的目标函数来制定适应度函数；然后，根据适应度函数值挑选个体参与遗传操作；最后，按照优胜劣汰和适者生存的生物学原理逐代进行衍化，直至得到问题的最优解或近似最优解。遗传算法具有自组织性、自适应性、并行性、过程性、不确定性等特点。这些特点使得遗传算法在优化问题中得到了极为成功的应用。但是，它也存在一些不足，如遗传算法的局部搜索能力很差，并极容易出现早熟现象，从而导致算法的收敛性降低［6］。

为克服遗传算法存在的缺陷，将免疫系统的相关理论引入到遗传算法的框架里，提出了1种新的算法——免疫遗传算法。免疫遗传算法是在遗传算法的基础上，借鉴生物免疫系统自适应识别和排除侵入生物体内的抗原性异物的功能，将生物免疫系统的学习、记忆、抗体多样性的特点引入遗传算法而得［7］。在实际问题中，免疫遗传算法将求解问题的目标函数对应于入侵生命体的抗原，问题的解对应为免疫系统产生的抗体，并通过一系列遗传操作及抗体亲和度的计算，在保持抗体多样性的基础上，找出针对问题的最优解［7］。总而言之，免疫遗传算法既保留了遗传算法随机全局并行搜索的特点，又在很大程度上避免过早收敛，确保收敛于全局最优解。

相较于遗传算法，免疫遗传算法具有以下特点［8］。

1）通过个体浓度评价可以对抗体进行促进和抑制，很好地保持了抗体的多样性，这样，能够增强算法的全局搜索能力，从而使算法收敛更快。

2）具有免疫记忆功能，该功能是免疫遗传算法的1个重要特色，可以使系统在处理同类问题时，使用记忆库中的个体作为初始群体，这样加快搜索速度，迅速收敛到全局最优解。

3）具有自我调节功能，可以提高局部搜索能力。

2.2 免疫遗传算法设计

1）编码设计。列车运行调整问题的解就是列车的运行时刻，因此采用实数编码，能够省去推算的过程，直接求得结果，简便可行。定义从午夜零点到某个时刻所经过的秒数代表现实中的相应时刻，如，6000代表着01：40：00。

文中的编码格式为：xk＝（，，…，），其长度为M×N×2。

2）适应度函数设计。适应度函数是衡量遗传算法中解的好坏的1种标准，个体的适应度值越大，表明解的性能越优。在遗传算法中，适应度函数一般是目标函数，为了便于操作，一般要求适应度值非负，而且适应度值增大方向必须对应目标函数优化的方向。因此，笔者设计的适应度函数如下。

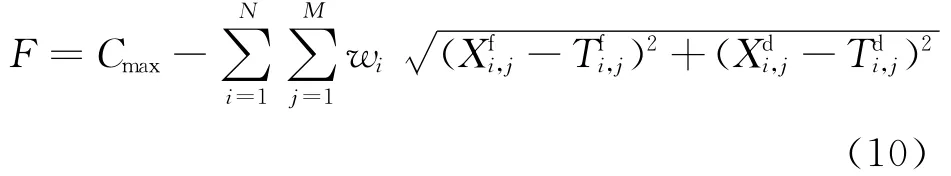
式中：Cmax为事先设定的一较大正数。

算法必须考虑对约束条件的处理，笔者采用罚函数法进行处理，即对解空间中无对应可行解的个体在计算适应度值时增加一个罚函数，降低该个体遗传到下一代的概率。第1个约束条件进行罚函数处理的过程如下

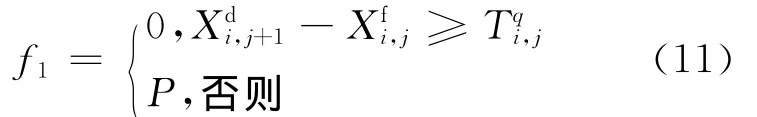
式中：P为一正数。

剩余的约束条件可依次进行，则经过罚函数方法处理得到的新的适应度函数为

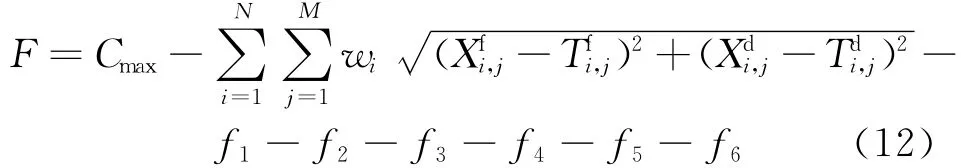
3）抗体浓度。抗体和抗体之间的亲和力反映了抗体之间的相似程度，此处借鉴由Forrest等提出的R位连续方法计算抗体与抗体之间的亲和力［9］。即

式中：ki，j为抗体i和j中相同的位数；L为抗体的长度。

亲和力越大，表明2个抗体之间的相似程度越高，当种群进入下一代时，亲和力大的抗体将会大肆繁殖，但是如果相似抗体太多，为了防止算法在小范围内进行复制，使得算法收敛于局部解，就要抑制它们的再繁殖，从而保证算法求解的范围比较广。选用浓度来决定抗体的促进和抑制。设Ci为抗体i的浓度，则浓度定义为

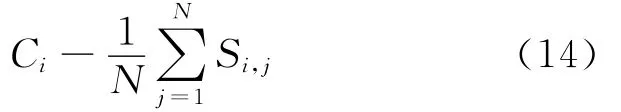
其中：τ为预先设定的阈值，一般取值范围为［0.9，1］.

4）抗体的抑制和促进。免疫遗传算法的选择概率不仅与个体的适应度有关，而且与抗体的浓度有关［6］。这是免疫遗传算法区别于遗传算法的1个重要特色。设抗体i的期望繁殖率为P，则其选择复制的概率为

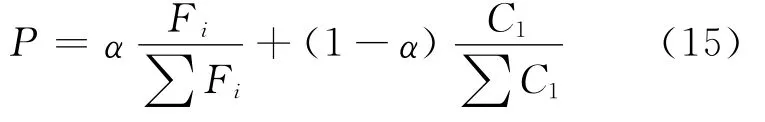
式中：α为常数。由上式可见，个体适应度越高，则期望繁殖概率越大；个体浓度越大，则期望繁殖概率越小。这样既鼓励了适应度高的个体，同时抑制了浓度高的个体，从而确保了个体多样性［9］。

5）选择操作。选择：按照轮盘赌选择机制和精英保留策略相结合的方式进行选择操作。精英保留策略是指群体中适应度最高的个体不进行交叉操作与变异操作，直接遗传到下1代种群中，目的是为了保证群体收敛到最优解。

轮盘赌选择是基于适者生存这一思想，按照期望繁殖概率进行选择。

6）交叉操作。是指从种群中选取2个个体，通过2个染色体的交换组合，从而产生下1代的新的个体。由于采用的是实数编码，因此采用实数交叉法，即染色体xi和染色体xj在随机选取的k基因位上进行基因交换，用数学公式可以描述为

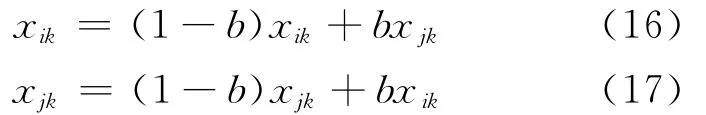
式中：b为随机数。

7）变异操作。变异操作是算法中很重要的一步，笔者采用混合变异算法，即采用基于实数编码的非均匀变异与边界变异法进行变异操作。将进化代数T分为2个阶段，当进化到当前代数t时，若0＜t＜T／2，时，采用非均匀变异算法，否则采用边界变异法。这样混合的变异方式可以提高算法的收敛速度，使算法尽快收敛于全局最优解。

2.3 免疫遗传算法的基本步骤

在上述内容的基础上，得到基于免疫遗传算法（调整算法）的步骤如下。

1）输入抗原。输入目标函数和各种约束条件，作为抗原。

2）产生初始抗体群。把抗体定义为列车运行调整问题的可行解，在解空间上，随机生成一定数目的个体。

3）计算适应度和浓度。计算抗体群中的适应度和浓度。

4）记忆细胞。先将适应度最高的若干个体放入记忆库中，再按照期望繁殖率将剩余的抗体选入记忆库，这些记忆库中的个体可以直接传递到下1代中。

5）抗体的抑制和促进。在免疫遗传算法中，适当地采用抑制策略以保持种群中抗体的多样性，在构造选择概率时，综合考虑适应度和浓度来实现。

6）新群体的产生。通过遗传操作，产生新1代的抗体。

7）终止条件判断。若满足终止条件，则输出结果，否则返回到步骤3）。

3 实例分析

以某双线自动闭塞铁路12：00～16：00时的10辆列车为例。在算法运行中，比较重要的参数有：交叉概率，变异概率，迭代次数，种群规模最大迭代次数等［10］。经过反复试验，本例参数设置为：迭代次数maxgen＝200，种群规模sizepop＝30，记忆库容量overbest＝10，交叉概率pcross＝0.8，变异概率pmutation＝0.1，多样性评价参数α＝0.9，浓度阈值τ＝0.9。应用免疫遗传算法进行计算，并将其与遗传算法的运行过程进行对比，结果见图1和图2。

由此可以看出，免疫遗传算法在40多代进行收敛，而遗传算法在60多代后曲线才收敛，显然，免疫遗传算法收敛速度较快。此外，免疫遗传算法收敛到最优解，而遗传算法只收敛到次优解，这说明免疫遗传算法能搜索到更优结果。

在进行试验时，同时对2种算法试验20次，发现遗传算法试验成功率仅为70%，而免疫遗传算法能达到100%。

综上所述，免疫遗传算法在收敛速度，最优值以及试验成功率方面都具有更为优越的特性。

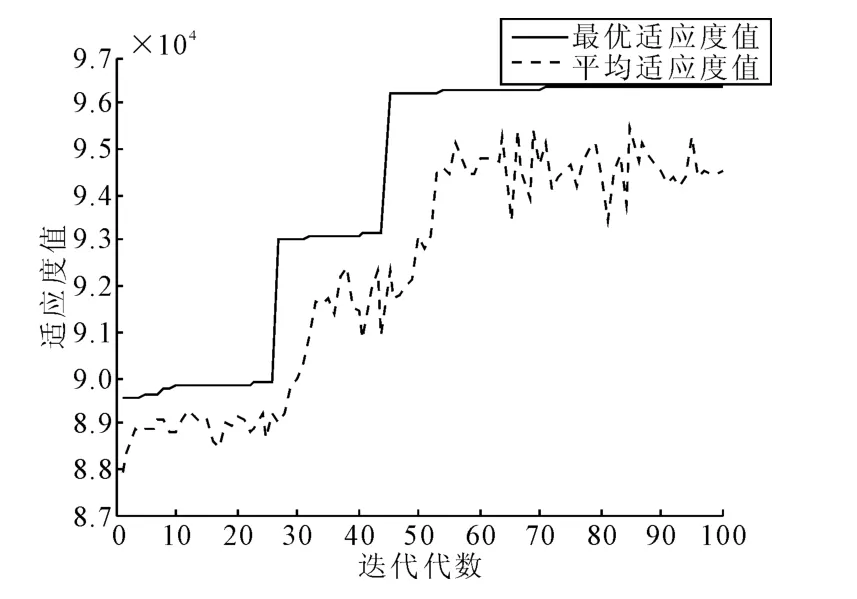
图1 免疫遗传算法收敛曲线Fig.1 The convergence curve of the immune genetic algorithm

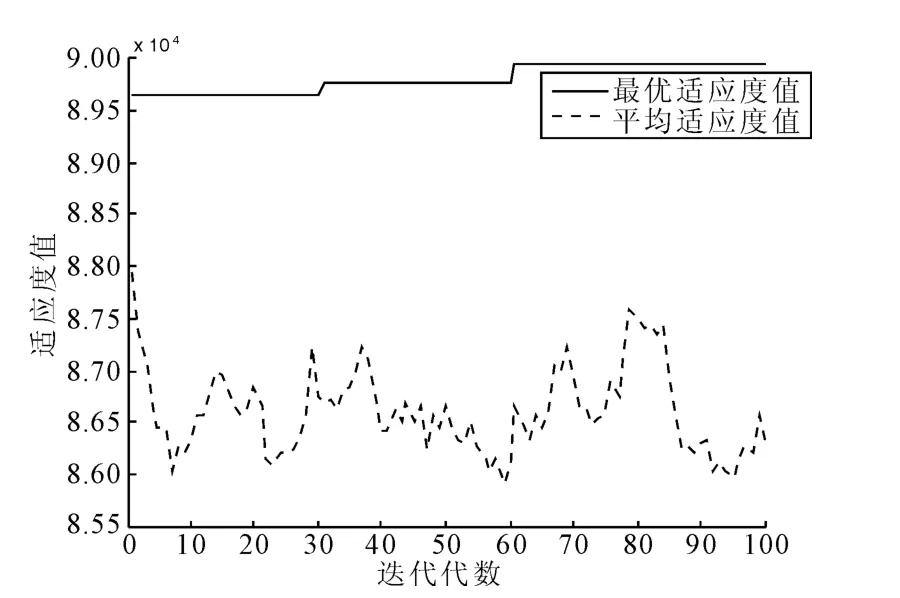
图2 遗传算法收敛曲线Fig.2 The convergence curve of the genetic algorithm

4 结束语

针对遗传算法在运用中存在的不足，选用1种免疫遗传算法进行列车运行调整问题的求解。列车运行调整模型的建立，突出了以偏离运行图最小为目标函数的特点，并充分考虑了区间运行时分、车站停车时分约束、越行约束等条件，在此基础上设计了免疫遗传算法的各个步骤。其中，适应度函数进行了罚函数方法处理，亲和度采用了不同于信息熵的R位连续方法进行计算，选择操作则是综合了轮盘赌选择机制和精英保留策略的方式，变异操作采用了混合的变异方式进行操作。仿真结果表明，免疫遗传算法在收敛速度，最优值甚至试验成功率方面都具有更好的性能。

［1］ 李志宏.列车运行智能调整系统相关问题研究［D］.成都：西南交通大学，2006.

［2］ 张翠平，曹成铉.列车运行调整的图论模型与启发式算法［J］.科学技术与工程，2010，10（10）：2560－2564.

［3］ 陈雍君.基于序优化方法的列车运行调整算法研究［J］.铁道学报，2010，32（3）：1－8.

［4］ 梁 旭，黄 明.现代智能优化混合算法及其应用［M］.北京：电子工业出版社，2011.

［5］ 豆雯雯.基于免疫蚁群算法列车运行调整模型的优化与研究［D］.兰州：兰州交通大学，2012.

［6］ 刘泉叮.基于免疫遗传算法的OD矩阵反推模型与算法［D］.重庆：重庆大学，2010.

［7］ 莫 军.基于免疫遗传算法的水下无人平台航路规划［J］.舰船科学技术，2012，34（9）：76－78.

［8］ 王宏刚，张 琦等.基于遗传算法的高速铁路行车调整模型［J］.中国铁道科学，2006，27（3）：96－100.

［9］ 史 峰.Matlab智能算法30个案例分析［M］.北京：北京航空航天大学出版社，2011.

［10］ 赵胜武，赵建武，林 杨.基于免疫遗传算法的公交线网优化研究［J］.交通信息与安全，2009，27（6）：43－47.