三参数区间灰数的距离熵模型及应用研究
2014-04-08胡丽平李炳军
王 娜,胡丽平,李炳军
(河南农业大学信息与管理科学学院,河南 郑州 450000)
在灰色决策理论与技术中,以决策信息为区间灰数情况下的研究最为活跃,相关研究成果不断涌现[1~5].然而,在区间灰数决策问题研究中,用区间灰数表示决策信息时,为了覆盖整个取值范围,区间灰数的上限与下限常常会取的过大,造成决策的不确定性程度增大.文献[6]提出了三参数区间灰数的概念,即除了取值区间外,还可以获知灰数的最可能取值点,为区间灰数决策问题研究指出了新的途径.此后,相继出现了一系列关于三参数区间灰数决策问题的研究成果.文献[7]通过构建三参数区间数,改进了项目决策评价方法;文献[8]探讨了方案指标值为区间灰数且灰数取值可能性最大数已知的决策问题;文献[9]提出了三参数区间值模糊集上的TOPSIS决策方法;文献[10]通过定义三参数区间数型偏好序之间的偏差函数,给出了一种确定决策者权重向量的有效方法;文献[11]提出了一种基于相对优势度的三参数区间灰数的排序方法,并应用于变量为三参数区间灰数数据包络分析模型;文献[12]建立了基于三参数区间数熵测度的属性权重模型,并构建了依据TOPSIS思想的不确定性决策框架.这些研究成果丰富和深化了三参数区间灰数决策理论,为本研究提供了借鉴.信息熵可表示系统的有序程度,用以解决信息的量化度量问题[13].近年来,信息熵已被广泛应用到多个行业,用来对不稳定数据进行修正,从而降低不稳定性对结果的主观性影响.本研究将三参数区间灰数决策问题与信息熵相结合,构建三参数区间灰数的距离熵模型,以期解决灰色决策问题中三参数区间灰数属性的赋权问题,并借助相关实例,验证模型的有效性和适用性.
1 三参数区间灰数及灰距离熵模型
1.1三参数区间灰数及运算
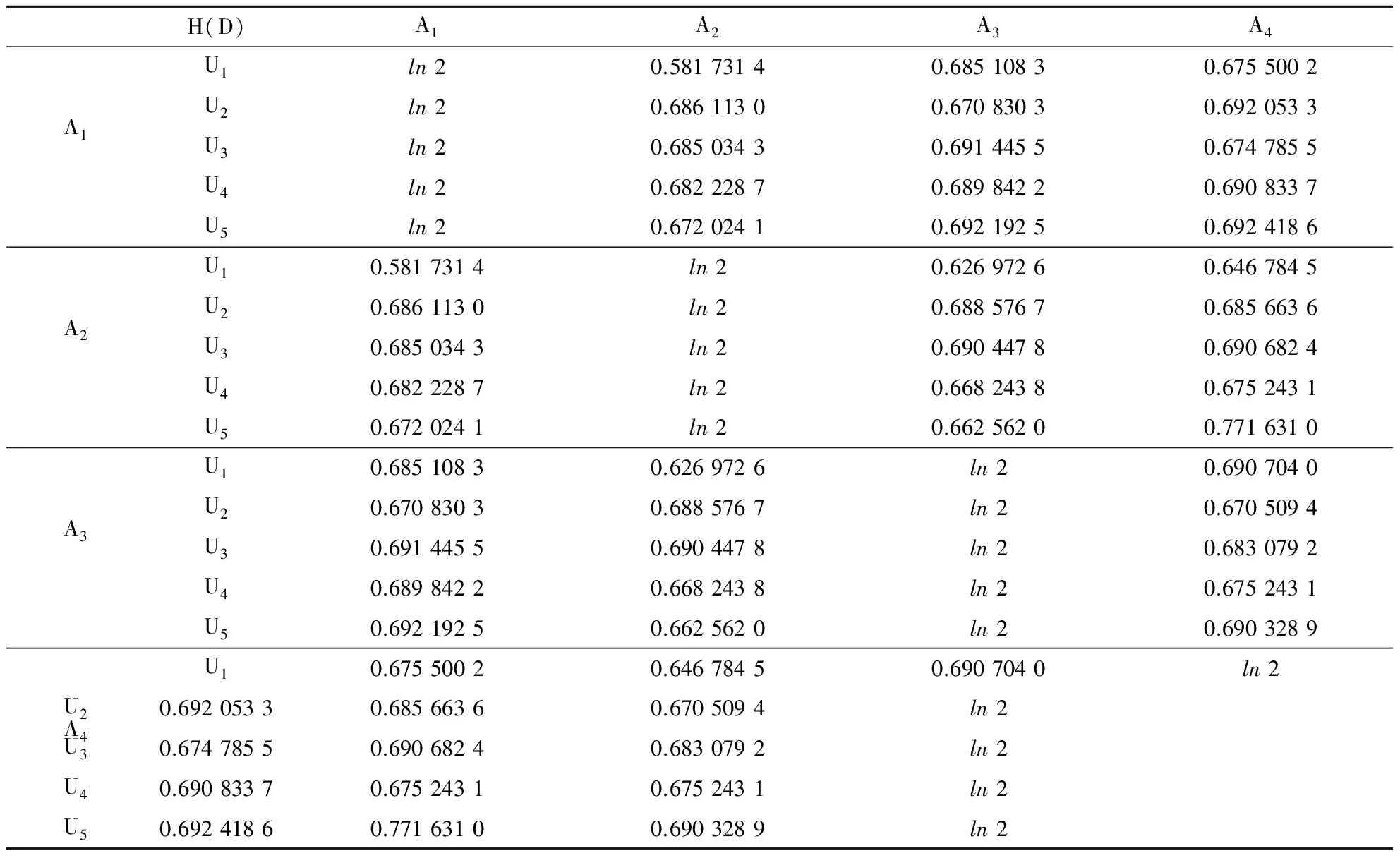
记x(⊗)∈[xL,x*,xU](0 类似于区间灰数的运算性质[14],可定义三参数区间灰数的运算.设a(⊗)∈[aL,a*,aU](0 加法运算:a(⊗)+b(⊗)=[aL+bL,a*+b*,aU+bU] 减法运算:a(⊗)-b(⊗)=[aL-bU,a*-b*,aU-bL] a(⊗)-a(⊗)=[aL-aU,0,aU-aL] 乘法运算: a(⊗)·b(⊗)=[min(aLbL,aLbU,aUaL,aUbU),a*b*,max(aLbL,aLbU,aUaL,aUbU)] 指数运算:ca(⊗)=[caL,ca*,caU],c为正实数,a(⊗)为正区间灰数 乘方运算:[aL,a*,aU]n=[(aL)n,(a*)n,(aU)n] 1.2三参数区间灰数距离熵 信息熵是信息论中的重要概念,是系统紊乱程度的测度.对一个具体的系统来说,如果这个系统随机性很大、非常混乱、毫无秩序,则此系统的信息熵就一定很大;反之,如果一个系统是确定的、具有一定的规则、服从一定的秩序,则此系统的信息熵就一定小.SHANNONCE[13]提出了信息熵的公式: (1) Pi表示随机事件i发生的概率;n表示事件的个数. 类似信息熵定义,参照[15]和[16],定义三参数区间灰数的距离熵.令a(⊗)=⊗1,b(⊗)=⊗2,a(⊗)和b(⊗)中的aL=a,a*=m,bU=b,bL=c,b*=n,bU=d,定义三参数区间灰数⊗1∈[a,m,b](0 (2) 为三参数区间灰数⊗1和⊗2的距离熵.灰距离熵不是⊗1和⊗2之间距离的大小,而是2者接近度的度量. 定理1三参数区间灰数⊗1和⊗2越接近,灰距离熵H(D)就越大,当⊗1=⊗2时(即a=c,b=d,m=n),H(D)最大;⊗1和⊗2越远离,H(D)就越小. H(d1)=-P1lnP1-(1-P1)ln (1-P1). 对H(d1)求P1的导数,H(d1)′=-lnP1-1+ln(1-P1)+1, 同理,b=d时,H(d2)最大,maxH(d2)=ln 2;m=n时,H(d3)最大,maxH(d3)=ln 2. 因此,当a=c,b=d,m=n时,距离熵H(D)最大, H(d1)]=ln 2. 同理可证,当⊗1和⊗2越远离时,H(D)就越小. 2.1三参数区间灰数决策问题及属性权重的确定 在多属性决策中,所有方案在同一属性下的属性值差异越小,则说明该属性对决策的影响越小;反之,则说明该属性对决策的影响越大.从这个角度考虑,方案属性值差异度越大的属性应赋予较大的权重.由三参数区间灰数距离熵的定义及定理1可知,三参数区间灰数⊗1和⊗2越接近,灰距离熵H(D)就越大,当⊗1=⊗2时,H(D)最大;⊗1和⊗2越远离,H(D)就越小.因此对于属性值是三参数区间灰数的多属性决策问题,其每一个属性值的差异性就可以用三参数区间灰数的距离熵来表示.对于属性Uj,若方案Ai与其他方案的偏差用Dij表示,可定义: (3) (4) 对于属性Uj而言,Dj表示每个方案与其他方案的灰距离熵总偏差.所有方案在属性Uj下灰距离熵偏差越大,说明该属性指标对方案决策和排序所起的作用越小;反之,所有方案在属性Uj下灰距离熵偏差越小,说明该属性对方案决策和排序所起的作用越大.因此,从对方案进行排序的角度考虑,方案综合属性值灰距离熵越小的属性Uj,就认为它辨识度越好,而尽可能地赋予它较大的权重.对所有的属性Uj,若使所有待评方案与其他决策方案的灰距离熵最小,则得到的各属性的权重一定是优化的,即属性权重的赋权模型为: (5) 2.2实例分析 某大型体育馆有A1,A2,A3,A44种备选方案,根据U1~U55种属性(属性分别为质量、成本、工期、安全、施工难度)进行决策,请多位专家分别给出权重区间和属性矩阵,各属性值以三参数区间灰数形式给出,则每个属性值权重的取值分别为: ω1∈[0.12,0.15], ω2∈[0.23,0.35], ω3∈[0.10,0.15], ω4∈[0.32,0.40], ω5∈[0.10,0.18]. 各方案的属性值如表1所示,数据来源于文献[7]. 表1 各方案属性值 归一化处理成标准区间数决策矩阵: 利用公式(2)计算各属性值下4种方案之间的灰距离熵,结果见表2. 表2 属性Uj的灰距离熵 基于表2,由式(3)和式(4)得: 7.813 602ω1(k≠i) 从而得: D=7.813 602ω1+8.187 492 6ω2+8.230 949 4ω3+ 8.193 477 6ω4+8.173 378 4ω5 由式(5),区间权重的赋权模型为: 应用LINGO程序,求解得到属性权重为: ω1=0.15,ω2=0.25,ω3=0.10,ω4=0.32,ω5=0.18. 这样,决策就转化为权重已知情况下的三参数区间灰数多属性决策问题,应用灰色多属性决策的理想解法[17],加权标准化决策矩阵为: 进一步求得,方案A1,A2,A3,A4的相对贴近度为: C1=0.514 4;C2=0.341 7;C3=0.655 4; C4=0.486 7. 根据相对贴近度的大小,各方案的最终排序为A3>A1>A4>A2.方案3为最优方案.与文献[7]结果一致.本研究运用灰距离熵模型对多属性决策的属性进行赋权,一定程度上减少了主观因素对权重的影响,使结果更为优化合理和说服力. 在现实决策问题中,三参数区间灰数广泛存在.本研究借助信息熵理论,建立了三参数区间灰数距离熵模型,证明了三参数区间灰数与灰距离熵之间的关系,及灰距离熵的相关性质.针对具有三参数区间灰数特征的多属性决策问题,根据离差最大化思想和三参数区间灰数距离熵模型,给出了一种新的属性赋权模型,并结合具体实例,验证了该赋权模型的适用性,为三参数区间灰数多属性决策提供了一种新的属性赋权方法.同时,本研究所建立的灰距离熵模型,也可应用于多属性决策问题的属性筛选,以及多指标评价问题的指标体系约简. 参考文献: [1]罗 党,周 玲,罗迪新.灰色风险型多属性群决策方法[J].系统工程与电子技术,2008,30(9):1674-1678. [2]陈孝新.一种基于证据推理的混合型灰色多属性群决策方法[J].控制与决策,2011,26(6):170-172. [3]胡军华,许 琦.基于前景理论的区间数多准则决策方法[J].统计与信息论坛,2011,26(9): 23-27. [4]CUI J,LIU S F,XIE N M.Novel grey decision making model and its numerical simulation[J].Transactions of Nanjing University of Aeronautics and Astronautics,2012,29(2):112-117. [5]王晓勇,楼佩煌,唐敦兵.基于信息量的不确定型多属性决策方法[J].运筹与管理, 2012,21(1):64-69. [6]卜广志,张宇文.基于三参数区间数的灰色模糊综合评判[J].系统工程与电子技术,2001,23(9):43-45. [7]戴 勇,范 明,姚 胜.引入三参数区间数的多属性项目决策及研究[J].决策方法研究,扬州大学学报:自然科学版,2006,9(3):21-23. [8]罗 党.三参数区间灰数信息下的决策方法[J].系统工程理论与实践,2009,9(1):124-130. [9]兰 蓉,范九伦.三参数区间值模糊集上的TOPSIS决策方法[J].系统工程理论与实践,2009,29(5):129-136. [10] 林 键,姜 永.基于三参数区间数型偏好序的群决策方法[J].山东大学学报:理学版, 2011,46(7):65-69. [11] 王洁方,刘思峰.三参数区间灰数排序及其在区间DEA效率评价中的应用[J].系统工程与电子技术,2011,33(1):106-109. [12] 闫书丽,刘思峰,朱建军,等.基于熵测度的三参数区间数信息下的TOPSIS决策方法[J].中国管理科学,2013,21(6):145-151. [13] SHANNON C E.A mathematical theory of communication[J].The Bell System Technical Journal,1948,27(3-4):373-423. [14] 罗 党.灰色决策问题分析方法[M].郑州:黄河水利出版社,2005. [15] 刘 伟,葛世伦,王念新,等.基于数据复杂性的信息系统复杂度测量[J].系统工程理论与实践,2013,33(12):3198-3208. [16] 王鹏飞,李 畅.不确定多属性决策双目标组合赋权模型研究[J].中国管理科学, 2012,20(4):104-108. [17] 丁进进.灰色多属性决策若干问题探讨[D].郑州:华北水利水电学院,2012.
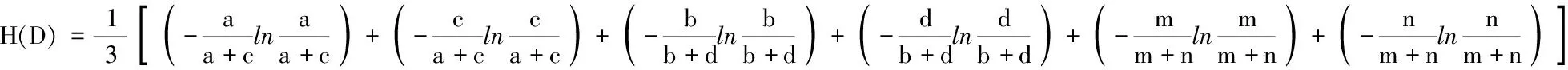
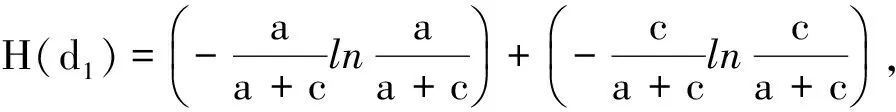
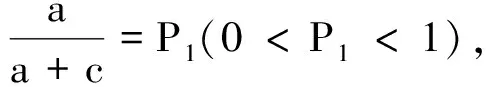
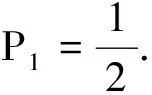
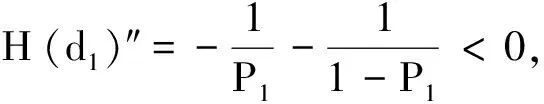
2 三参数区间灰数距离熵的应用
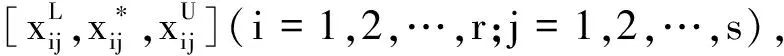

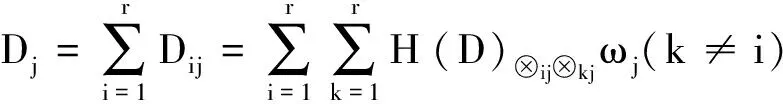




3 结语
