三维模型特征点曲度球面调和表达

屠 宏，耿国华

(西北大学信息科学与技术学院可视化技术研究所， 陕西 西安 710127)

三维模型作为继音频、图像以及视频之后的第4种多媒体形式受到了越来越多的关注，并且其在工业设计、虚拟现实、游戏动漫等方面的应用也越来越广泛.随着三维数据获取技术、三维建模以及计算机软硬件技术的快速发展，三维模型的大量获取变得容易.目前许多科研机构都建立了大型的三维模型库，如何在大型三维模型库中快速、准确的找到自己所需的三维模型，成为多媒体信息检索中的一个重要课题.目前，常用的三维模型检索方式主要包括文件名匹配、基于内容的检索、基于语义的检索.后2种检索方式是目前的研究热点. 本研究提出的三维模型检索方法属于基于内容的检索的范围.许多学者在基于内容的三维模型检索方面作了大量的研究工作.PETIT等[1]利用优化的形状平面分层次的表达了三维模型，提高了三维模型检索的查准率，然而此方法的时间复杂度较高，且算法过程较复杂；WU等[2]利用几何驱动法检索医学三维模型；NELSON等[3]首先将球面调和的方法应用于三维模型的形状分析，将三维模型看做被平面区域参数化的曲面，进而在参数域中对其进行球面调和分析；ERTURK等[4]首次使用球面调和分析的方法提取三维模型特征，但是他使用的是距离作为调和函数，使得检索的查全率较高，但是查准率较低.随着三维模型数量、质量和检索技术的提高，对检索系统的查准率的要求也在提高.因此，基于局部特征的三维模型检索算法迅速发展起来[5～8].模型的局部特征易受噪声的影响，种类较多；提取一种鲁棒的、能真实反映模型局部特征的描述符是一项具有挑战性的工作. 本研究定义了一种新的局部特征描述符——曲度，曲度包含了平均曲率和高斯曲率的信息，通过球面调和分析，以弥补平均曲率和高斯曲率自身的缺点，从而显著提高检索算法的查准率.

1 曲度的提出

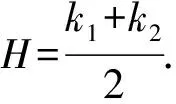
基于这种情况，本研究提出了一种新的度量刻画曲面的弯曲程度，即曲度.

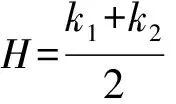
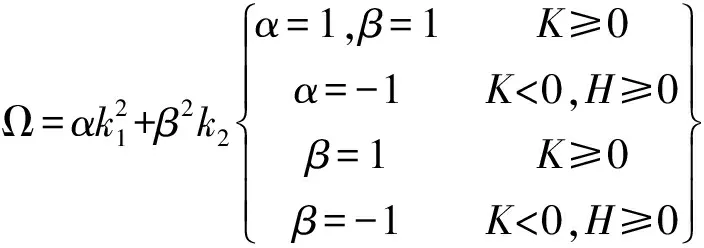
(1)

式中：Ω为曲面的曲度,α,β分别为调和系数.

2 三维模型曲度的球面调和表达

2.1三维模型特征点的选取

在对三维模型进行预处理后，使用单位球体将其包裹，单位球体的球心与三维模型的质心重合.从球心向外发射射线，其与三维模型的交点为特征点.该点在球坐标的表示为： (rsinθcosφ,rsinθsinφ,rcosθ)，其中θ∈[0,π]，φ∈[0,2π].由于是单位球，半径r=1，因此毎个点的坐标为(sinθcosφ,sinθsinφ,cosθ).具体的实现方法为：xij=(sinθicosφj,sinθisinφj,cosθi)，其中θ=(2i+1)π/2n，φ=(2jπ)/n，i,j=0,1,2,…，n.

2.2三维模型特征点的曲度计算

根据公式(1)和三维模型主曲率的具体情况推导出曲度的3种表达.

1)α=1,β=1:

(2)

2)α=1,β=-1:

(3)

3)α=-1,β=-1:

(4)

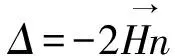
则(θ,φ,Ω)构成函数关系，即f(θ,φ)=Ω，该函数的散度为0，即：2f=0

用球面坐标表示为：

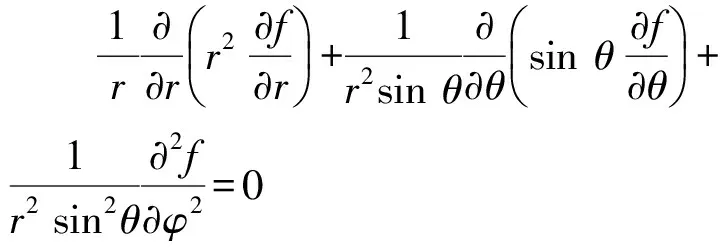
(5)

利用分离变量的方法可以得到以上方程的解为：

(6)

(7)

式中：Pnm为协同勒让德函数.

这样，就可以提取Hm,n作为模型的特征.进而使用欧式距离进行匹配.

3 检索试验结果分析

本研究在Windows平台上实现了一个3D模型检索的试验系统， 使用数据库为普林斯顿大学的PSB,从中选取1 000个模型作为试验数据库(包括动物、人物2类).检索接口使用模型输入接口,试验系统实现了高斯曲率调和方法(X)、平均曲率调和方法(Y)以及本研究采用的曲度调和方法(Z)，并采用查全率与查准率作为评价3种方法的依据. 对同一输入模型分别使用高斯曲率、平均曲率以及曲度进行调和分析，并分别使用2组特征进行检索试验，根据验结果绘制了PR(查准率-查全率)曲线(图1).检索结果动物类模型和人物类模型的前6个模型见图2和图3.研究结果表明，本研究的方法明显优于另外2种调和方法.

图2列举了以动物类模型Input_1为输入模型，分别以高斯曲率、平均曲率以及曲度为其特征的检索结果,并列举了3种方法检索后结果排在前6位的模型.输入模型包含的节点较多，在节点处曲率变化较大，对于此类模型，曲度和高斯特征检索效果应优于平均曲率的检索效果，试验结果也验证了这一推断.平均曲率特征检索出1个问题模型.在检索结果排序方面，高斯曲率和曲度为特征的检索结果排序更合理.

图3列举了以人物类模型Input_2为输入模型，分别以高斯曲率、平均曲率以及曲度为其特征的检索结果，并列举了3种方法检索后结果排在前6位的模型.输入模型近似圆柱体，曲率分布较均匀，多处高斯曲率为0，对于此类模型，曲度和平均曲率为特征的检索效果应优于高斯曲率.试验结果验证了这一推断.高斯曲率特征检索出2个问题模型，其检索性能不如平均曲率和曲度特征.

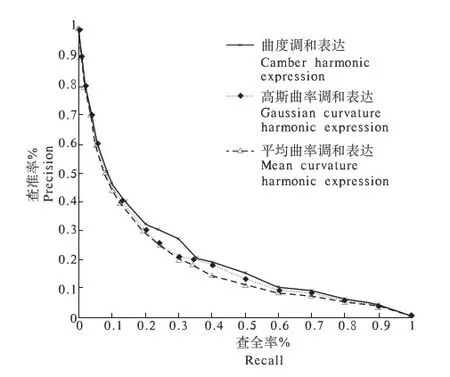
图1 3种方法的查准率-查全率曲线

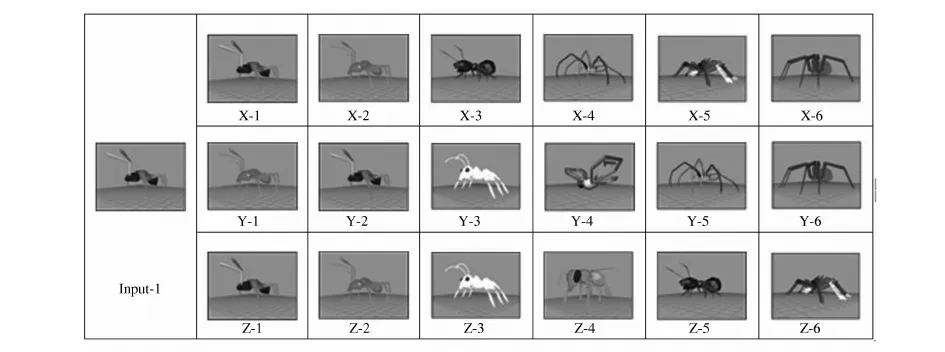
图2 动物类模型的检索结果

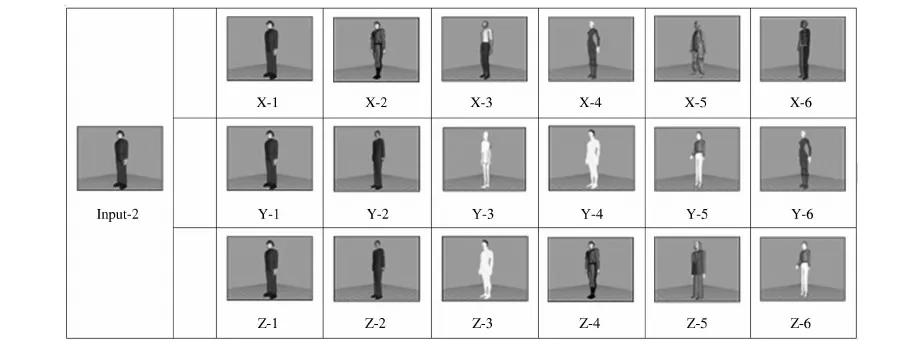
图3 人物类模型的检索结果

三维模型特征点的平均曲率描述了通常意义下的弯曲程度，但是当模型平滑区域较大时，特征点平均曲率的方差较小，对不同三维模型的敏感度较低；高斯曲率可以理解为最大与最小法曲率的加权值，其对模型上的鞍点不敏感(复杂模型鞍点较多).本研究定义的曲度特征描述符很好的克服了平均曲率与高斯曲率的缺点，更好的表达了三维模型特征点的局部特征，取得了较好的检索效果.

4 结语

本研究提出了一种新的曲面弯曲程度度量——曲度.曲度较精确的描述了三维模型特征点的局部特征，真实、全面的放映了模型曲面的弯曲程度.试验结果表明，采用曲度作为调和函数检索三维模型取得了较好的检索效果.但是，特征点曲度的计算依赖于2个主曲率的计算，而在离散的网格曲面上，主曲率的计算容易受到噪声的影响且计算较复杂.另外，曲度值Ω∈[0,1]，因此计算机的截断误差也会影响曲度的计算精度.随着计算机硬件技术的提高，曲度值的计算也会越来越精确.曲度是一种局部特征，采用曲度作为三维模型的特征描述符主要提高了检索的查准率，如果要全面的检索三维模型必须配合全局特征.以后应在曲度特征的基础上，需找合适的全局特征与之配合使用，建立更完善的特征描述符进行检索，进而得到更好的检索效果.

参考文献：

[1]PETIT S F,WU B,KAZHDAN M,et al. Increased organ sparing using shape-based treatment plan optimization for intensity modulated radiation therapy of pancreatic adenocarcinoma[J]. Radiotherapy and Oncology,2012,102(1): 38-44.

[2]WU B,RICCHETTI F,SANGUINETI G,et al. Patient geometry-driven information retrieval for IMRT treatment plan quality control[J]. Medical Physics,2009,36(12): 5497-5505.

[3]NELSON L,GETZOFF D E . Spherical harmonic molecular surfaces[J].IEEE Computer Graphics and Applications,1988,8(4): 42-50.

[4]ERTURK S ,DENNIS T J. 3D model representation using spherical harmonics[J].IEEE Electronics Letters,1997,33(11): 951-952.

[5]LIU Z B,BU S H,ZHOU K,et al. A survey on partial retrieval of 3D shapes[J]. Journal of Computer Science and Technology,2013,28(5): 836-851.

[6]BAE M S,PARK I K. Content-based 3D model retrieval using a single depth image from a low-cost 3D camera[J]. Visual Computer,2013,29(8): 555-564.

[7]CHEN Q,FANG B,YU Y M,et al. 3D CAD model retrieval based on the combination of features[J]. Multimedia Tools and Applications,2014,36: 1-19.

[8]DYN N,HORMANN K,KIM S J,et al. Optimizing 3D triangulations using discrete curvature analysis[J]. Mathematical Methods for Curves and Surfaces,2001,28(5)： 135-146.