多航段舱位控制与定价策略
2014-04-07刘长有
周 蔷,刘长有
(1.南京航空航天大学民航学院,江苏南京210016;2.中国民航大学空中交通管理学院,天津300300)
0 引言
为了合理地优化配置航空运输资源,有关航班在非热点城市实行航班转机运输已成为航空运输与相关组织研究的一大热点,这就形成了多航段舱位控制问题。单航段航线只需要考虑一个起点的收益与座舱分配问题,而多航段在考虑起飞点的同时,还必须兼顾中转点的顾客及收益问题。航空公司力求从收益管理的角度出发,对起飞点与中转点进行统一考虑,实现整体利润的最大化。1972年,文献[1]就单航段、两级票价价格的舱位控制问题提出了边际收益的概念。1987年,文献[2]提出了边际期望座位收益方法(EMSR),这种方法已经成为各航空公司舱位控制的经典方法。1995年,文献[3]就需求函数是一般函数的情形提出了两级票价结构的收益管理模型。文献[4-5]在文献[3]的基础上,又考虑了风险因素及多种票价,提出了另外一种两级票价结构的收益管理模型,最后还证明了最优价格仅能从给定价格集的子集中取得,这一理论被称为最大凹向包络理论。2004年,文献[6]根据最大凹向包络理论分析了单航段的航空公司收益与舱位控制问题。对于多航段舱位控制的研究国外起步较早,也已经有了很多成果,而国内还处于起步阶段。2005年,文献[7]根据遗传算法构建了航空收益管理中的多航段舱位控制模型,但舱位的嵌套控制问题没有在这个模型中被考虑到。2010年,文献[8]针对航空货运收益,提出了基于椭球体的多航段舱位控制稳健优化模型,并结合粒子群算法求解。2012年,文献[9]对航空收益管理的研究现状进行了归纳。近年的多航段舱位控制研究,大多使用人工智能优化算法,此类算法需要反复迭代,计算量较大,一般不考虑舱位的嵌套控制问题。
本文将同时考虑多航段航空客运中的价格收益与舱位控制问题,将每个航段上的舱位视为独立的个体,然后根据最大凹向包络理论以及连续系统动态规划理论,分析研究多航段航班的动态价格与舱位控制,提出了一个考虑舱位价格嵌套的多航段舱位控制及定价策略模型。
1 问题描述与模型
目前的EMSR方法能很好地计算单航线的收益,是因为单航线是基于航段与航线的统一,也就是说,如果能保证航段收益的最大化,也就等同于保证了航线的最大化,但对于多航段的航班来说,单一航段收益的最大化可能与航线收益最大化是相互矛盾的[10]。在这种情况下,有必要提出适合多航段的舱位控制与收益模型,来保证多航段航班在整个航线上能实现收益的最大化。
设某航班的座位总数为M,舱位等级数为K,客流类型(不同航段上的客流)数为N,飞机起飞时间为T。对于属于第n类客流的第k个舱位等级给定的可行价格集合为Pnk= { p,,…,p,其中,mnk为第n类客流第k个舱位等级的可行价格数目,则假定:
设到时刻t为止,第n类客流的剩余可售座位数为Sn(t),λ(t)为对应p的需求密度函数,则时刻t舱位等级k在航段n上的价格与舱位分配的统一策略可表示为:
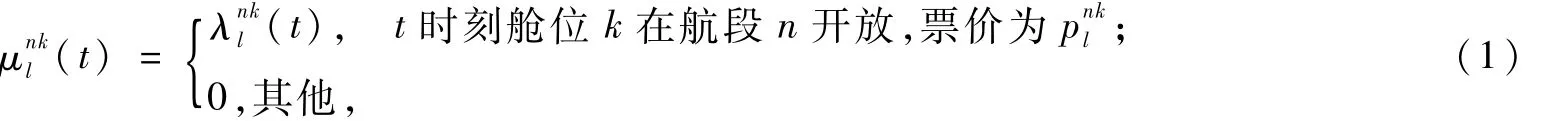
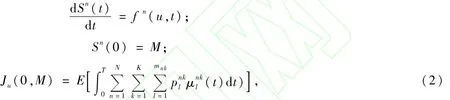
其中,fn(u,t)容易得到,实例分析中将给出仅一个中转点(即航段数为3)时的形式。根据连续控制系统动态规划理论,可构建Ham ilton-Jacobi方程[6,11-14]:
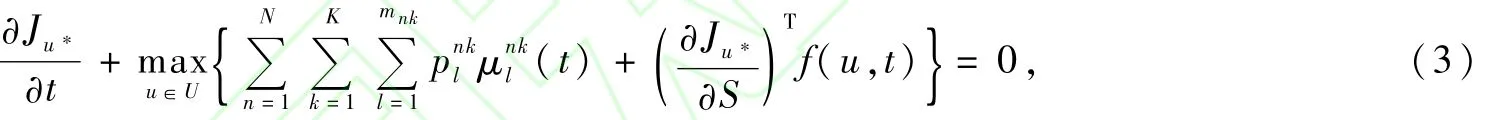
其中,S=(S1(t),S2(t),…,SN(t))T;f=(f1(u,t),f2(u,t),…,fN(u,t))T。由于座位数为整数,则可用差分形式离散化。求得,再根据边界条件即可求得Ju*,从而得到最优策略u*。
2 模型求解
对于本文的多航段航线的收益与舱位控制模型,结合文献[5]的最大凹向包络理论和Ham ilton-Jacobi控制方程来求解。文献[6]在单航段航线的定价策略研究中使用了类似方法,本文将其推广到多航段航线问题中。
第1步:利用最大凹向包络理论确定各航段各舱位的最优价格集。文献[5]证明,对于任一价格集合,存在最大凹向包络子集,最优价格只能从该子集中产生。
若t时刻航段n舱位等级k开放,最优价格只从Pnk的子集P中选择,最优价格集P满足以下性质:(Ⅰ)r(λ)是λ的递增凹函数,其中=;(Ⅱ)对应任一集合P,P⊂P⊆Pnk,P对应的r(λ)为λ的非递增凹函数;(Ⅲ)若∉P,则在任意时刻,均不开放。为便于表述,后文均假定P={,,…,}。
第2步:舱位控制。根据Ham ilton-Jacobi方程(见式(3))可得:

代入fn(u,t)的表达式可得,如果t时刻航段n舱位等级k开放,则其充要条件为:

第3步:开放舱位最优价格选择。文献[5]导出了单航段某个舱位等级某种价格被选择的充要条件。结合最大凹向包络子集性质,推广到多航段问题,则在t时刻航段n舱位等级k以价格p开放的充要条件为:

3 实例分析
某航空公司有一条从广州-武汉-西宁的航线,执行该航线的飞机有商用座位数为150个,其中舱位等级有公务舱与经济舱两种。为了方便计算,对每个航段进行编号,其中广州-西宁为1,广州-武汉为2,武汉-西宁为3。表1给出了各个航段各个舱位的价格集,以及对应的需求密度,并计算出了价格和需求密度的乘积(收入)。

表1 价格-需求密度表
3.1 求解最优价格集
作出收入与需求密度的关系图,如图1所示,利用最大凹向包络理论可得,航段n舱位等级k的最优价格集P为:
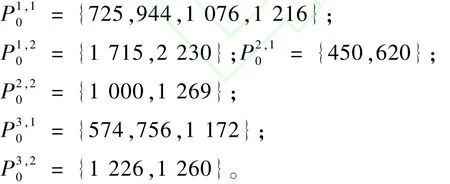
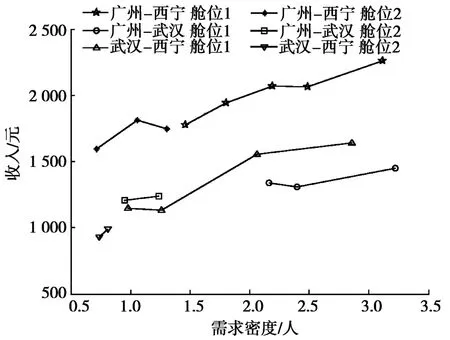
图1 收入(r)-需求密度(λ)关系图
3.2 求解Ham ilton-Jacobi方程
下面给出Hamilton-Jacobi方程的具体形式,首先需确定方程(2)中的fn(u,t)。为简化求解,航班“广州 -武汉 -西宁”可看成“广州-武汉”“武汉 -西宁”两段单航线,“广州-西宁”可由这两段单航线组合而成,则方程(2)的fn(u,t)为:

由于航段1可看成由航段2和航段3组合而成,故简化掉了f1(u,t),而Sn(t)(n=2,3)可理解为航段2和航段3上空闲的座位数。再给出的差分离散化形式:

其中,Ju*(t,M2,M3)表示当t时刻航段2、3空闲座位数分别为M2、M3时,从t到T时刻的最佳收益。将方程(7)和方程(8)代入式(3)即可得到Hamilton-Jacobi方程,再导出方程(6)所表示的各个价格开放的充要条件:

易得Hamilton-Jacobi方程的边界条件:①Ju*(t,0,0)=0;②Ju*(T,M2,M3)=0,在T的一左邻域内,所有舱位以最低价开放。求解Ju*,即可得到u*。对于Ju*(t,M2,0)和Ju*(t,0,M3)可看成单航段问题,文献[6]给出了具体的求解步骤,在此不作详述。对于M2,M3>0的情形,根据常数变异法,可写出方程通解为:
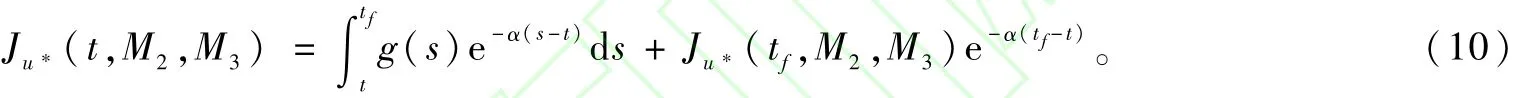
若在[t,tf]内u*与t无关(因u是取值离散的,u*必为分段与t无关的函数),则

[0,T]可分解为若干个区间[t,tf]进行求解,区间内u*与t无关,区间边界u*跳变,求解方法是文献[6]的单航段的求解方法的推广,篇幅限制不作详述。从M2,M3=0开始递推,即可计算出任意M2,M3>0的Ju*,最终计算得Ju*(0,M,M)为问题解。
3.3 算法稳定性分析
座位数较多时,方程(10)需采用数值积分求解。从tf=T递推计算每个区间[T,t1f],[t1f,t2f],[t2f,],…,[,0],需分析此递推过程的稳定性。根据方程(9)和方程(10)有:


说明若误差恒为正(或负),前一计算误差无缩小无放大地叠加到后一计算结果中,算法不稳定;若误差正负值交错出现,正负相抵,算法稳定。因而,求解过程要使误差正负等概率。

根据方程(10)可得:则方程(10)的递推过程是稳定的,即随着M2,M3的增加,前面计算的误差衰减。
3.4 求解结果
利用Matlab软件编程求解舱位控制与最优价格策略,求解得到在预剩余售期为T、剩余座位数为150时的最优价格策略,如表2所示。
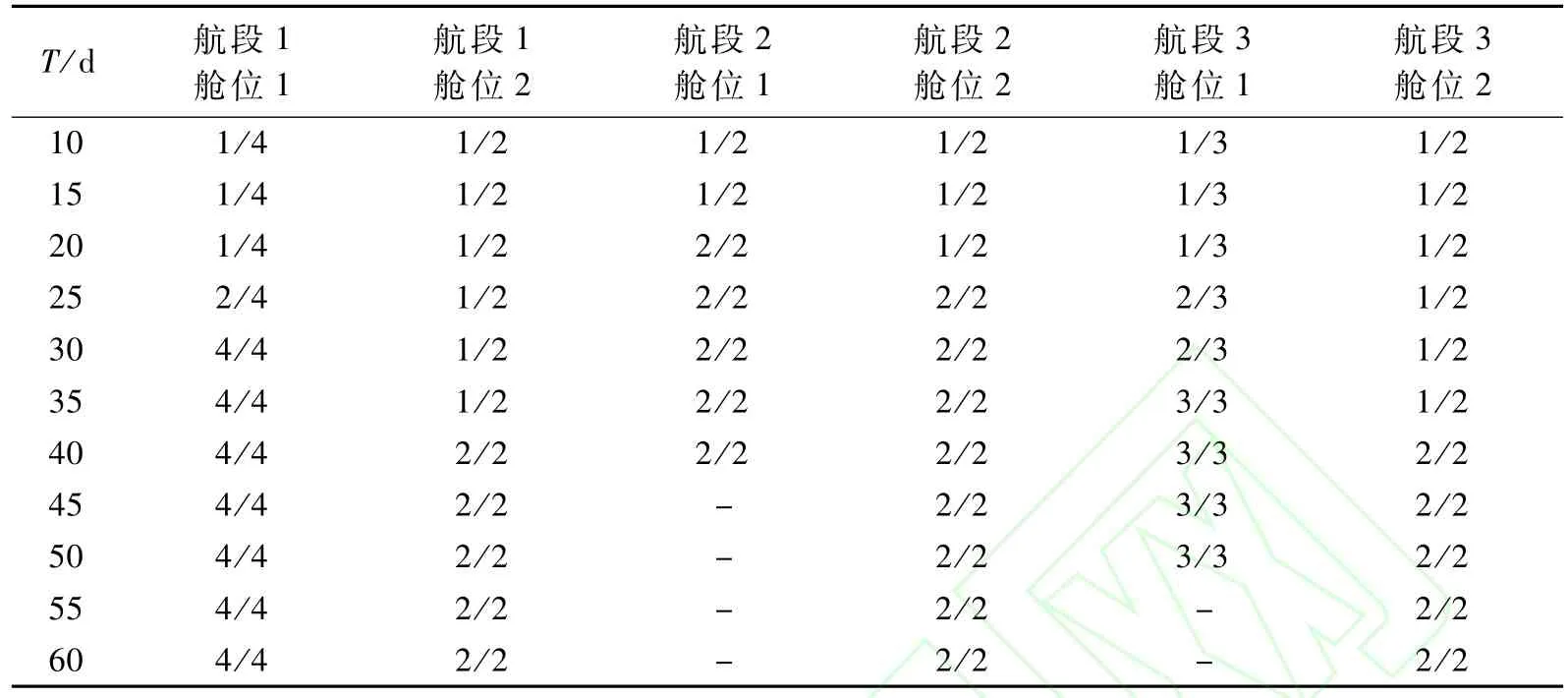
表2 不同剩余预售期下的最优价格策略
从表2可看出:剩余预售期增大,最优价格倾向较高价,这是由于剩余预售期越大,售完全部座位要求的需求密度越小,则可以选择较高的价格,以获得较大的收益。由表2还可看出:剩余预售期增大到一定程度时,有部分航段部分舱位不开放售票,这是由于剩余预售期较长时,停止部分收益率较低的舱位的售票,同样能把全部座位售完,以获得更大收益。以上分析可见,求解得到的最优价格策略与实际相符。
3.5 仿真模拟
为了验证最优价格策略的最优性,同时分析最优价格策略下的售票特性,对售票过程进行蒙特卡罗仿真模拟。
为验证最优价格策略的最优性,设待出售总座位数为150,在不同预售期长度下,分别使用最优价格策略、最高价格策略和最低价格策略进行20次仿真,计算得不同价格策略下20次仿真的平均总收益,如图2所示。
为观察最优价格策略下不同航段的售票状况,设待出售总座位数为150,在不同预售期长度下,采用最优价格策略进行20次仿真,计算得不同航段20次仿真的平均售票量和平均收益,如图3和图4所示。

图2 不同预售期长度下,3种售票策略的总收益
从图2可看出:在不同预售期长度下,最优价格策略的总收益始终大于最高和最低价格策略,体现了最优价格策略的优越性。由图2还可看出:预售期长度较短时,3种策略的总收益相差不大。这是由于预售期较短时,最优价格策略接近最高价格策略,而最高价格策略出售的票量较少,最低价格策略出售的票量较多,从而使三者结果相差不大;当预售期大于20 d时,最低价格策略的总收益不再随着预售期增大,这是由于20 d足够以最低价售完所有票,预售期大于20 d,较高的价格策略将可获得更高的收益;当预售期大于100 d后,最优价格策略的收益不再增加,因而最佳预售期长度为100 d。
从图3可看出:总体上,航段1“广州-西宁”的售票量最多,航段2“广州-武汉”次之,航段3“武汉-西宁”售票量最少,这是由于“广州-西宁”为始发-终点站航段,收益较大,应更多出售始发-终点站航段机票。
从图4可看出:航段1的收益明显大于航段2和航段3的收益,这与图3的分析结果一致,因而应更多地出售收益较大的始发-终点站航段机票。
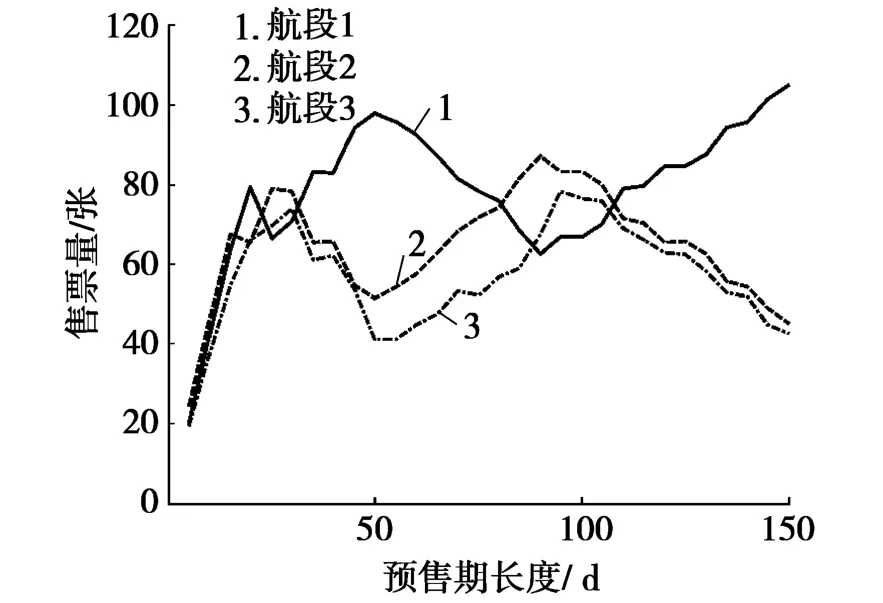
图3 不同预售期长度下,3条航段的最优售票量
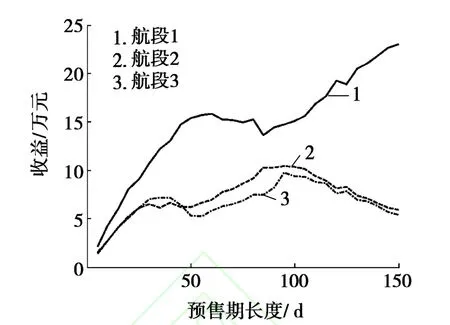
图4 不同预售期长度下,3条航段的最优收益
4 结论
本文基于收益管理的思想,以航空客运中的多航段航线的收益最大化为目标,采用最大凹向包络理论与Hamilton-Jacobi控制方程建立了多航段航线的动态价格与舱位控制分析模型,该模型能根据剩余售票时间、剩余座位,以及不同航段上的需求量,决定任意时刻每个舱位是否开放,以哪种价格开放。最后通过实例分析表明:模型能为多航段航线的舱位分配及价格的制定提供一个快速有效的决策参考,可推广到更多航段的情形。
[1] Littlewood K.Forecasting and Control of Passengers[C]//12 th AGIFORSSymposium Proceedings.1972:103-105.
[2]Peter P B.Air Travel Demand and Airline Seat Inventory Management[D].Cambridge:Massachusetts Institute of Technology,1987.
[3] Feng Y,Callego G.Optimal Stopping Times for End of Season Sale and Optimal Stopping Times for Promotional Fares[J].Management Science,1995,41:1371-1391.
[4] Feng Y,Xiao B.Optimal Policies of Yield Managementwith Multiple Predetermined Prices[J].Operation Research,2000,48:332-343.
[5] Feng Y,Xiao B.A Continuous-time Yield Management Model with Multiple Prices and Reversible Price Changes[J].Management Science,2000,46(5):644-657.
[6] 李晓花,萧柏春.航空公司收入管理价格与舱位控制的统一分析[J].管理科学学报,2004,7(6):63-69.
[7] 高强,朱金福,陈可嘉.航空收益管理中的多航段舱位控制模型[J].交通运输工程学报,2005,5(4):82-85.
[8] 衡红军,李雅静.多航段舱位控制稳健优化模型研究[J].计算机工程与设计,2010,31(12):2887-2893.
[9] 李金林,雷俊丽,冉伦,等.航空收益管理柔性舱位控制机制的研究现状与展望[J].北京理工大学学报,2012,32(4):331-347.
[10] De B S V,Freling R,Piersma N.Mathematical Programming for Network Revenue Management Revisited[J].European Journal of Operational Research,2002,137(1):72-92.
[11] 朱金福,刘玮,姚韵.航空客运舱位控制和超售综合动态建模研究[J].系统工程学报,2007,22(5):525-531.
[12] 巨永峰,李登峰.最优控制[M].重庆:重庆大学出版社,2005:159-167.
[13] 王莉莉,刘艺程.管道航路激活费用问题优化研究[J].河南科技大学学报:自然科学版,2013,34(1):41-44.
[14] 乐美龙,张健泽.航班超售与舱位控制综合优化[J].河南科技大学学报:自然科学版,2013,34(3):25-29.
