基于模糊广义预测控制算法的ATO系统仿真研究

顾桂梅蒲松芝

（1.兰州交通大学自动化与电气工程学院，730070，兰州；2.卡斯柯信号有限公司，200070，上海∥第一作者，副教授）

基于模糊广义预测控制算法的ATO系统仿真研究

顾桂梅1蒲松芝2

（1.兰州交通大学自动化与电气工程学院，730070，兰州；2.卡斯柯信号有限公司，200070，上海∥第一作者，副教授）

针对ATO（列车自动运行）系统的特点，设计了基于模糊广义预测控制算法的速度控制器，并结合实际线路建立了线路模型，生成了优化的目标曲线。利用Matlab分别对基于模糊广义预测控制算法和基于隐式广义预测控制算法的速度控制器进行了仿真。仿真结果表明，基于模糊广义预测控制算法的速度控制器不仅能使ATO系统的性能得到优化，而且在一定程度上削弱了坡道对列车运行速度造成的影响，具备良好的可移植性。

列车自动运行；模糊广义预测控制；仿真

First-author's address School of Automation and Electrical Engineering，Lanzhou Jiaotong University，730070，Lanzhou，China

列车自动运行（ATO）系统不仅能自动控制列车运行，减轻司机负担，而且能在保证列车安全运行的前提下，提高列车运行的各项性能，因此得到广泛关注，针对ATO系统的研究也取得了不少成果。然而，由于列车运行过程十分复杂且极易受环境因素影响，因此很难找到精确的数学模型。模糊广义预测控制（FGPC）算法是一种将模糊逻辑和广义预测控制（GPC）算法相集成的控制策略。该算法对被控过程模型要求不高，且能进一步提高系统的稳态精度，减小动态误差［1］。为此，本文将FGPC算法应用到ATO系统中。Matlab仿真结果表明，该算法能减弱或消除坡道对列车运行速度造成的影响。

1 ATO系统的设计

1.1 速度控制器的结构

ATO系统的性能指标包括运行的安全性、准时性，以及停车精准性、节能性和乘客舒适性。指标的好坏与系统对速度的控制密不可分，因此，对ATO仿真系统的设计，核心是对速度控制器的设计［2］。

根据系统功能、FGPC算法理论及机车实际特点，设计列车速度控制器（如图1所示）。首先，速度控制器对目标曲线进行柔化处理，得到参考轨迹并将其作为控制器的输入；其次，将广义预测控制器的输出作为列车运动模型的输入，并控制列车运行速度；其三，将当前时刻列车实际速度与目标速度进行比较，构成偏差向量；最后，将偏差向量及偏差变化量进行模糊推理并对预测误差加以补偿，即作用在列车运动模型上的控制信号u（t）由广义预测控制量u1（t）和模糊控制量u2（t）两部分组成，使列车实现无误差运行。这种将模糊推理和GPC算法组合的方法不仅提高了系统的鲁棒性，而且降低了对预测模型精确度的要求，对列车运行这样的复杂系统具有实际价值。

为提高ATO系统的适应性，在图1中，将线路坡道对列车运行速度的影响作为扰动量加入控制器中。因此，反馈的实际运行速度包括列车在GPC算法控制下对参考轨迹的追踪速度和环境因素对列车造成的干扰速度。模糊推理不仅对GPC误差进行补偿，还对环境引起的干扰速度进行补偿，从而降低了环境对列车运行速度的影响。

图1 速度控制器的设计

1.2 列车运动模型

广义预测控制是以受控自回归积分滑动平均模型（CARIMA）为基础的一种控制算法。设被控对象的数学模型采用如下的CARIMA方程描述：

A（z-1）y（k）=B（z-1）Δu（k-1）+ξ（k）/δ （1）其中

式中：

u（k），y（k）---分别为被控对象的输入和输出；

δ---差分算子，δ=1-z-1；

ξ（k）---均值为零、方差为σ2的白噪声。

为了使控制效果更加良好，在实际确定目标函数时，需考虑当前时刻的控制对系统未来时刻的干扰。目标函数为

式中：

n---最大预测时域；

m---控制时域；

λ---控制加权系数。

Δu（k+j-1）=0表示在m步后控制量不再变化。

GPC算法的控制目标是使被控对象输出值y（k）尽量靠近预定值yr（k）。在实际中，控制目标不是使y（k）直接跟随yr（k），而是追踪参考轨迹w（k+j）。参考轨迹为：

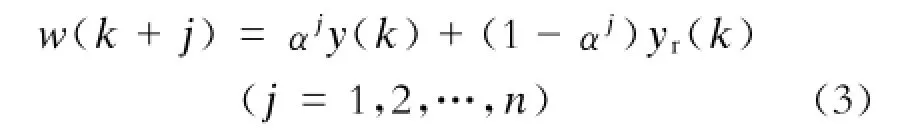
式中：

α-柔化系数，0＜α＜1。

由式（2）和式（3）可知，GPC算法的最终目的是通过Δu（k），Δu（k+1），…，Δu（k+m-1）的求解使得目标函数达到最小值。

要完成对ATO系统的仿真，首先要有列车运动模型作为控制对象。在此，对文献［3］中列车运动模型进行离散变换，并考虑坡道对列车运行的影响，确定速度控制器的输出差分方程为：

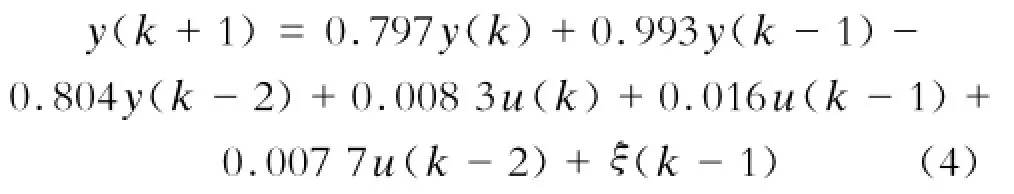
式（4）中，ξ（k-1）表示k-1时刻坡道对列车速度的干扰量。将列车运动模型的差分方程转换为广义预测CARIMA模型为：

其中：

1.3 线路模型

在图1中，将坡道对列车的影响作为干扰速度叠加在控制器上。因此，设计线路模型的最终目的是将坡道对列车产生的附加阻力转换为速度形式。

1.3.1 线路参数的化简

城市轨道交通线路由各种不同的线路条件组合而成，为减少工作量，在实际计算中需对坡道进行化简。化简坡道可由式（5）求出［4］。

式中：

i1，i2，…，in---各实际坡道坡度千分数；

l1，l2，…，ln---各实际坡道长度；

H1，H2---化简后坡道的始点和终点标高；

ih---化简后坡道坡度千分数；

lh---化简后坡道长度。

本文以上海轨道交通16号线惠南站到惠南东站上行为例，结合式（5）对坡道进行化简。

1.3.2 坡道附加阻力及其转换

坡道附加阻力是列车在坡道上运行时，其重力在沿下坡道方向的分力引起的。根据文献［4］，可得列车的坡道附加阻力为：

式中：

Wi---坡道附加阻力；

i---坡道坡度千分数；

g---重力加速度；

M---列车质量；

G1---列车所受重力；

θ---坡道夹角。

列车运行时的动能主要包括列车线性运动的动能和列车旋转部分的转动动能。

式中：

Ek---列车动能；

I---列车旋转部分转动惯量；

Rh---旋转部分换算半径；

w---列车旋转部分角速度，w=v/Rh；

γ---回转质量系数，是列车旋转部分的动能折算质量与列车全部质量的比值。

列车在坡道上运行，可将坡道产生的附加阻力视为独自作用在匀速运行列车上的合力。根据牛顿第二定律，结合式（6）和式（7），可得坡道附加阻力对列车运行产生的干扰速度为：

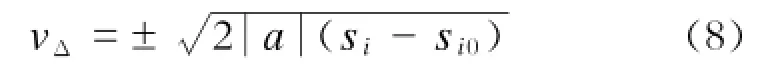
式中：

si---当前列车所在里程；

si0---列车所处坡道开始里程；

a---坡道附加阻力产生的加速度。

根据式（8），可得化简后坡道产生的速度干扰曲线，如图2所示。

图2 坡道产生的干扰速度曲线

分析图2可知，由于单质点列车模型忽略了列车的长度和车辆间的相互作用力，因此当列车跨越换坡点时，列车受力是瞬时变化的，从而导致了干扰速度的瞬时变化。

1.4 目标曲线的生成

速度控制器的功能是确保列车能很好地跟随目标曲线运行。当提供给速度控制器的目标曲线较差时，无论设计的速度控制器性能多好，也不能使ATO系统获得良好性能。这就要求供给速度控制器的目标曲线必须是一条最优的曲线。为提高系统节能性，本文在生成目标曲线时采用了节能策略。即：加速阶段以最大牵引力加速，中间阶段尽可能地延长列车匀速运行或惰行时间；进站阶段以最大制动力制动［5］。

在线路模型中，由于条件限制，区间被分为120 km/h和100 km/h两个限速不同的区段，进、出站限速为80 km/h，线路总里程为5 899 m。根据列车运动模型、线路模型及操纵策略得到列车运行过程理想的v-s目标曲线如图3所示。

图3 v-s目标曲线图

列车跟随目标曲线可能存在超调量，在设计目标曲线时，取区间最大仿真运行速度分别为32 m/s（区间最高限速）和26.5 m/s（曲线区段限速），进、出站最大运行速度为20.8 m/s，稍低于ATP（列车自动保护）系统给出的线路限速33.33 m/s、27.78 m/s和22.2 m/s。

1.5 参数的确定

GPC算法是基于参数模型的控制算法，模型参数的选取对速度控制器的控制性能会产生极大影响。对于模糊控制器来说，输入、输出变量的模糊论域及量化因子、比例因子等参数对系统的控制性能有着十分重要的影响，因此需要对这些参数进行说明。

1.5.1 广义预测控制参数的选取

根据文献［6］，在选择预测时域长度n时，必须使其超过受控对象的时滞和惯性部分。n的取值越大，系统的抗干扰和抗模型失配能力越好，但n取值太大会增加计算量，故取n=9。控制时域长度m取值越大则跟踪性能越好，但取值太大会导致系统不稳定，此处取m=2。控制加权系数λ用来限制控制增量Δu的剧烈变化，取λ=2。柔化系数α取值越大，系统的鲁棒性越好，但取值太大会导致系统的快速性降低，故取α=0.92。采样周期T过大会使受控模型不准，控制效果下降，T太小则会造成控制器延时，影响系统的稳定性，本文结合ATO系统的特点，取T=5。需特别说明的是，在选择采样周期时，为改善启动阶段的估计和控制，可首先测出对象的单位阶跃响应系数，以此作为初始参数。

1.5.2 模糊控制参数的选取

1.5.2.1 模糊语言变量的语言值分档

本文采用二维模糊控制结构，选取预测输出与参考轨迹的偏差e、偏差变化量ec作为模糊输入量，模糊控制量u2作为输出量。

模糊输入量的物理论域上下限分别为预测输出与参考轨迹的误差、误差变化量中的最大值和最小值；模糊控制量的物理论域取为u2=［-10，10］。两个模糊输入变量、输出控制量的模糊论域分别为［-6，6］和［-9.333，9.333］。模糊控制器的输入变量e、ec及输出变量u2的模糊子集均为｛NB，NM，NS，ZO，PS，PM，PB｝，含义依次为负大、负中、负小、零、正小、正中、正大。

1.5.2.2 模糊子集隶属函数的确定

根据系统特性，选用均匀分布的三角形函数作为模糊输入隶属函数，非均匀分布的三角形函数作为模糊输出隶属函数，且隶属度函数的中心值分别为［-6，-4，-2，0，2，4，6］和［-6，-2.667，-0.667，0.667，2.667，6］。图4、图5分别为输入变量模糊子集隶属函数和输出变量模糊子集隶属函数。

图4 输入变量e、ec模糊子集隶属函数

图5 输出变量u2模糊子集隶属函数

1.5.2.3 模糊控制规则的确定

为了使系统更好地利用模糊控制器的反馈补偿作用，必须认真分析模糊控制器的输入变量，并结合列车操作者的工作经验建立模糊规则库，本文以表1为模糊规则。

表1 模糊控制规则表

2 仿真结果

2.1 未考虑坡道时的仿真结果

图6为不考虑坡道的情况，且列车分别在GPC隐式算法和FGPC算法的控制下跟踪v-t目标曲线运行时的仿真结果。GPC算法参数已在前文做介绍。模糊控制的量化因子为ke=0.714，kec= 5.12，比例因子为ku=2.14。

图6 追踪v-t目标曲线仿真图

分析图6可知，前50 s，列车在GPC隐式算法的控制下运行时，列车速度变化缓慢，不能快速地跟随目标曲线，跟踪误差较大；经过模糊控制量的补偿作用后，速度控制器不仅能快速跟踪v-t目标曲线，减小跟踪误差，还能确保列车准时到站；同时，当列车在区间低限速区运行时，基于FGPC算法的速度控制器能更好地保证列车运行的安全性。由此可知，基于FGPC算法的速度控制器能很好地优化ATO系统的性能。

图7为不考虑坡道的情况，且列车分别在GPC隐式算法和FGPC算法的控制下跟踪a-t目标曲线运行时的仿真结果。其中，GPC算法参数与跟踪vt目标曲线时相同，模糊控制的量化因子为ke= 7.13，kec=6.67，比例因子为ku=2.14。

图7 追踪a-t目标曲线仿真图

由图7可知，在50～100 s、180～200 s的时间段内，列车在基于GPC隐式算法的速度控制器下运行时跟踪误差基本为0；但在第25 s和220 s时，列车经过模糊控制量的补偿后能快速跟踪目标曲线，减小了跟踪误差，增强了系统的动态性和实时性。因此，基于FGPC算法的ATO系统具有更好的性能。

2.2 考虑坡道的仿真结果

以图2中化简后的第二个坡道为例进行仿真，验证本文设计的速度控制器在有坡道的线路上也能满足ATO系统的各项性能指标。化简后的第二个坡道为下坡道，坡长为1 350 m，坡度为4‰，坡道的起始位移为240.3 m。图8为列车分别在有坡道与无坡道情况下运行时的仿真曲线图。由图8可知，当列车运行至240.3 m处时，由于下坡道的存在，列车运行速度迅速增加，不仅超出了目标曲线，而且超越了限速曲线。因此，需对坡道产生的速度影响进行补偿控制。

图8 存在坡道干扰时v-s曲线图

图9为经过模糊补偿之后的仿真曲线图。在模糊控制量的补偿作用下，仿真曲线满足了低于限速曲线的要求，保证了列车的安全运行，使系统的性能得到了很大提高。由图9可以看出，应用FGPC算法设计的速度控制器能适应任何线路情况，能保证列车的安全运行且具有可靠的跟随性。

图9 有坡道时FGPC算法仿真曲线图

图10为速度控制器在FGPC算法控制下，列车分别运行在无坡道和有坡道线路上的仿真曲线图。当列车在有坡道的线路上运行时，列车运行速度变化较慢，但整体的跟随效果与在无坡道的线路上运行时基本相同。虽然其牺牲了ATO系统部分的快速性，降低了系统的响应速度，但确保了列车运行的安全性、平稳性和舒适性，体现了基于FGPC算法的速度控制器的良好性能。

图10 有坡道、无坡道时速度跟随曲线

3 结语

本文根据ATO系统的性能设计了基于FGPC算法的ATO系统速度控制器，并根据列车运动模型及线路模型生成优化的目标曲线。通过系统仿真，并与GPC隐式算法的控制效果进行比较，证明了将FGPC算法应用于ATO系统是可行的，且该算法不仅能改善ATO系统的各项性能指标，还能改善坡道对列车运行速度的影响，具有很好的移植性和适应性。

［1］ 宫赤坤，华泽钊.基于模糊补偿的广义预测控制［J］.吉林大学学报，2002，32（2）：78.

［2］ 黄秀玲，王长林.广义预测控制算法在ATO速度控制器中的研究［J］.轨道交通纵横，2009，1（5）：13.

［3］ 刘智勇.高速磁浮列车安全速度曲线算法及紧急制动控制研究［D］.杭州：浙江大学，2008.

［4］ 石红国.列车运行过程仿真及优化研究［D］.成都：西南交通大学，2006.

［5］ 崔世文，冯晓云.列车优化操纵与自动驾驶模式的研究与仿真［J］.铁道机车车辆，2005，1（10）：1.

［6］ 李国勇.智能控制及其MATLAB实现［M］.北京：电子工业出版社，2005：289.

［7］ 宗明，张国侯.轨道交通列车自动运行仿真平台的开发研究［J］.城市轨道交通研究，2012（6）：52.

Simulation of ATO System Based on Fuzzy Generalized Predictive Control Algorithm

Gu Guimei，Pu Songzhi

According to the characteristics of automatic train operation（ATO）system，a speed controller of ATO system based on fuzzy generalized predictive control algorithms（FGPCA）is designed，a line model combined with the actual lines is established and an optimized target curveis generated.Then the speed controller based on FGPCA and implicit generalized predictive control algorithms with MATLAB issimulated.The result proves that the speed controller based on FGPCA could not only optimize the properties of ATO system，but could also weaken the impact of ramps on the train speed to some extent.Therefore，this newly designed speed controller has a good transportability.

automatic train operation（ATO）；fuzzy generalized predictive control；simulation

U 231.6

2012-06-18）