基于改进粒子群算法的制造单元构建方法研究*

徐立云 荣 巨 郭昆吾 李爱平

(同济大学现代制造技术研究所，上海 201804)

为适应目前多品种、少批量的市场需求，单元化制造模式应运而生，它融合了job-shop 高柔性与flowshop 高生产率的特点，使传统生产方式下生产率与生产柔性之间的矛盾得到较好解决［1］。实施单元化生产的关键是制造单元的构建，即如何将一个给定的制造系统划分成若干个制造单元。国内外学者对制造单元的构建问题进行了较多研究，制造单元的构建技术主要有图论方法、数学规划方法和启发式算法等［2-3］。王建维［4］提出了一种基于模糊C 均值算法划分制造单元的方法;金哲等［5］提出了一种用排队论构建制造单元的方法;李淑霞等［6］提出了一种基于敏捷制造单元的车间动态重构方法，通过聚类算法对车间制造资源进行选择组织。但这些方法大多侧重对已有的制造资源进行聚类划分，而车间物流因素对单元构建问题的影响是不容忽视的。本文利用并行工程的思想，综合考虑了单元内与单元间的物流情况以及设备单元分组和单元内设备的具体排序，建立了相应的优化模型。针对求解模型，设计了具有交叉算子的改进粒子群优化(improved particle swarm optimization，IPSO)算法，构建制造单元。

1 问题描述

制造单元构建问题是通过对所加工的工件进行工艺分析，将所有工件和所需的加工设备进行分组，形成特定的工件族和与之对应的设备组，每一工件族和相对应的设备组即构成一个特定的制造单元［7］。良好的单元构建工作一般要考虑到两方面的内容，一是单元的独立性，即要使单元工件的全部加工工序所包含的设备都在一个单元内，这样可有效减少工件在单元间的移动;二是单元的紧凑性，即同一单元内的设备在布置时，使设备间的间距尽可能小，以减小单元内的物流平均距离。但单元构建时考虑的这两方面内容在某种程度上又是矛盾的，所以在单元构建过程中，一般单元紧凑性通常是通过限定单元尺寸这一约束条件来实现［8］，文献［9 -10］认为，单元内部及单元之间的物流搬运费用可以作为单元构建的有效评价指标。

本文要解决的制造单元构建问题可以描述为:已知加工设备的数量，工件的种类，加工批量，工件的加工工艺路线以及每道工序所需要的设备，通过确定车间内所有设备的分组与单元内设备的具体排列顺序，以单元内部与单元间的物流搬运费用最小化为目标，完成制造单元构建。

2 数学建模

现有加工设备M 台，待加工工件种类及其加工批量等工艺参数均已知。为了描述方便，引入以下相关参数变量:p 为工件编号，p=1，2，…，P;m 为设备编号，m=1，2，…，M;c 为单元编号，c=1，2，…，C;k 为设备位置编号，k=1，2，…K;Vp为工件p 的生产批量;Hp为车间使用的搬运设备一次可以容纳工件p 的数量;Vp为工件p 的生产批量;CAp为单位物流量工件在单元内单位距离的顺流搬运成本;CBp为单位物流量工件在单元内单位距离的逆向搬运成本;CXp为单位物流量工件在单元间的物流成本。

2.1 设备间物流量的计算

设备间物流量和几个参数有关:工件的生产批量、搬运设备单次搬运的工件数量、工件加工过程需在设备间移动的次数。因此，对于工件p 而言，先后访问相邻两道工序的设备m 和m'，在设备m 和m'间引起的物流量的计算公式为:

其中:Lpmm'为0 -1 辅助变量，表示m 和m'是否为工件p 工艺路线上需要连续访问的两台设备，若是，则Lpmm'=1，Lpmm'=0 表示其他情况;npmm'为工件p 的加工过程中需要在m 与m'间移动的次数，若工件p 的工艺路径为1 -4 -3 -2 -1 -4，此时n1，4=2，n4，3=n3，2=n2，1=1;符号表示向上取整。

2.2 单元内单位物流量的搬运费用计算

为了简化，本文假定:(1)制造单元内均采用线型布局;(2)在制造单元内部，相邻两设备的中心间距D是相等的;(3)单元内部均是单一方向的物流。

故在计算中需要考虑物流方向对物流搬运费用的影响，单向线性布局中物流方向分为顺向与逆向两个方向，从上游设备向下游设备的流动称为顺向，反之则称为逆向或物流回溯。物流回溯会降低单元内的搬运效率，且其产生的单位物流费用也比顺向物流费用要高(CAp＜CBp)。

综上所述，考虑物流回溯对物流费用的影响，则单元内单位流量工件p 的工艺路径上，设备m 和m'间的物流搬运费用为:

xmc=1 表示设备m 属于单元c，xmc=0 表示其他;ycmk=1 表示设备m 被布置在单元c 的位置k 上，ycmk=0 表示其他。

2.3 单元间单位物流量的搬运费用计算

单元构建阶段还没有涉及到单元间的布局情况，故单元间物流距离无法获知，因此单元间的物流费用也就无法求出。文献［11］认为当单元尺寸变化在一定范围内时，单元间单位物流费用近似为一个常量。对于单元内部的物流距离以及费用情况，由公式(2)可以求出，而对单元间的物流费用需要进行估算。为简化起见，本文采用与文献［12］类似的策略，设单元之间单位物流量费用为常数CXp，即Cpmm'=CXp。

2.4 数学模型

制造单元构建的目标就是单元内部设备间与单元间的物流搬运费用最小化，数学模型如下:

决策变量:

约束条件:

约束(4)和(5)表示每一台设备只属于一个制造单元，而每一个单元最少包括两台设备，约束(6)与(7)则限制一个位置空间上只能放置一台设备，一台设备只能被放置于一个位置空间，约束(8)表示对单元数的限制。

3 算法设计与求解

3.1 基本粒子群算法

PSO 算法最早是由Kennedy 和Eberhart 在1995年提出，该算法源于对鸟类捕食行为的研究，通过模拟鸟集群飞行觅食的集体协作行为，使群体达到最优的目的。

PSO 算法中，每个优化问题的解都被看作是搜索空间中的一只鸟，称为粒子，每个粒子都有自己的位置和速度(决定飞行的方向和距离)，以及一个由优化函数决定的适应度值，其值的好坏表示粒子的优劣。粒子在解空间中运动，通过跟踪个体极值点(用pbest表示其位置)和群体极值点(用gbest表示其位置)更新个体位置。个体极值点(pbest)是指个体经历位置中计算得到的适应度值最优解;群体极值点(gbest)是指种群中所有粒子搜索到的适应度最优解。在找到这两个最优解后，每个粒子根据式(9)～(11)来更新自己的速度和位置。

3.2 改进粒子群算法

基本PSO 算法的搜索过程很大程度上置于一个位置空间，每个位置空间上有且仅依赖个体最优解和全局最优解，其搜索区域受到个体最优解和全局最优解的限制，比较容易陷入局部最优解。针对基本PSO 算法的不足，借鉴进化算法的思想，将进化算法中的交叉操作与基本PSO 算法进行混合，对交叉算子进行非线性设计，使得交叉率随种群中个体的适应度值的变化而变化，两个不同的粒子可以进行信息交换，增加了粒子“飞行”到搜索空间其他新位置的能力，避免粒子群过早地陷入局部最优。因此，其交叉率为:

式中:Pc为交叉率;favg为每代群体的平均适应度值;fmax为当前群体中最大的适应度值;f'为要交叉的两个粒子中较大的适应度值;pcmax与pcmin分别表示交叉率值的上限和下限，φ 为设定的常数。为改变交叉点的随机性和盲目性，根据父代粒子的适应度值来控制交叉点的位置。具体实现过程为:随机从种群中抽取要交叉的两个个体，假定其适应度值分别为f1、f2，则交叉点的串长为:

式中:l 为粒子长度。

3.3 粒子的编码与解码

PSO 算法的模型是在实数连续空间搜索，而制造单元构建问题的模型是属于离散空间的解。因此，需要设计合适的PSO 编码来完成连续空间的粒子与离散空间的单元组合进行映射。

PSO 算法中可以用二进制、实数和实值等对粒子进行编码。对于本文研究的问题，设计的粒子编码方式需要划分出单元个数的同时要确定设备在单元中具体的排列顺序。因此，本文将粒子编码分为两部分。

(1)设备位置的编码(Mpos) 采用实数编码方式，长度为设备的数量M，每个编码位对应一台设备，编码直接采用设备编号，这样粒子可以更直观地表达单元内设备的排列顺序。

(2)单元分割点的编码(Cdiv) 这一部分是长度为(M-1)，数值范围为［0，1］的实数编码串。

解码时，对各编码位上的数值进行四舍五入操作，用函数round 表示。规定round(xid)=1 的编码位为一个单元的分割点。这两部分的编码结合起来可以确定出单元的划分以及单元内设备的具体排列顺序。

如图1，现有8 台设备其位置编码为(8，1，4，5，3，2，7，6)，单元分割点编码为(0.22，0.35，0.76，0.15，0.17，0.96，0.41)，解码后为(0，0，1，0，0，1，0)。单元分割点解码后有两个“1”，将所有设备分为3 个单元，其中单元1 由设备“8，1，4”组成，单元2 由设备“5，3，2”组成，单元3 由设备“7，6”组成。设备编码段的编码顺序也决定了设备在单元内的布置顺序。

3.4 IPSO 算法的流程设计

采用IPSO 算法求解制造单元构建问题，算法流程

图1 粒子位置编码格式

设计如下:

步骤1 初始化，设定加速度因子c1和c2，最大迭代次数Tmax，将当前迭代次数设置为t=1，初始化粒子位置和速度;

步骤2 计算当前所有粒子的适应度值;

步骤3 判断是否达到最大迭代次数，若是，停止迭代，输出结果;否则，转向步骤4;

步骤4 按式(9)～(11)对粒子的速度和位置进行更新;

步骤5 比较当前粒子适应度值与个体最优值pbest，如果当前粒子适应度值比pbest更优，则更新pbest;

步骤6 比较当前粒子适应度值与群体最优值gbest，如果当前粒子适应度值比gbest更优，则更新gbest;

步骤7 随机找出两个需要交叉的粒子按照IPSO算法进行交叉操作，交叉率和交叉串长分别按式(12)、式(13)来确定，交叉操作后转向步骤2。

4 应用实例

4.1 实例描述

为响应市场需求的快速变化，某企业拟新建一加工车间，决定采用单元化生产模式。现有各种型号的车床、铣床、刨床、钻床、磨床等加工设备共20 台，待加工工件为6 种柴油发动机相关零配件，其生产批量以及工艺路径等工艺信息如表1 所示。制造单元构建时需要对这些设备进行分组，并以单元内部与单元间的物流搬运费用最小化为目标，构建制造单元。

表1 生产任务信息表

4.2 案例求解

(1)粒子的编码

本文采用实数编码的方式，将粒子编码分为两部分，即设备位置的编码和单元分割点的编码。每个粒子的结构由设备位置信息和单元分割点信息组成，其表现形式如3.3 节图1 所示。

(2)初始种群的生成

采用随机产生初始种群的方法构造初始群体。案例中，机床数为M=20 台，根据本文所采用的编码策略，随机产生的一组初始种群为:

(3)粒子的解码

本文所采用的解码策略，是对单元分割点所对应的粒子编码进行解码，用函数round 对各编码位上的数值进行四舍五入操作。因此初始种群里粒子编码结构的单元分割点解码为C'div(0，0，0，1，0，1，0，0，0，1，1，0，0，1，0，0，1，0，0)。

(4)适应度计算

本文的目标函数是求搬运费用的最小值，所以根据适应度函数特点，设置其为目标函数的倒数，即:

其中LC 为粒子i 的目标函数。由函数关系知，适应度值fitness(i)与目标函数LC 成反比，目标函数值越小，粒子的适应度越高，粒子更容易接近个体极值点和群体极值点。

(5)速度和位置的更新

粒子在解空间中运动，通过跟踪个体极值点和群体极值点更新个体位置。每个粒子根据式(11)～(13)来更新自己的速度和位置。

(6)粒子速度和位置的交叉操作

利用交叉操作，使两个不同的粒子进行信息交换，以增加粒子“飞行”到搜索空间其他新位置的能力，避免粒子群过早地陷入局部最优。根据本文编码的特点和意义，将粒子的交叉操作分段进行。对设备位置段采用部分映射交叉法(PMX)处理，对单元分割点段采用算术交叉方法处理。

①设备位置段的交叉操作假设选出的粒子对如图2 所示，计算得到交叉点串长为6，进行交叉操作后得到的原始子代如图3 所示。交叉操作得到的原始子代，产生了非可行解，使得粒子编码串不能完整表达设备编号，故需确定两个子串的映射关系:5 ＜-＞13，3＜-＞19，4 ＜-＞1，20 ＜-＞7，8 ＜-＞11。根据映射关系去除非可行解，得到的子代如图4 所示。

图2 父代粒子串

图3 原始子代粒子串

图4 修正后的子代粒子串

②单元分割点段交叉操作采用算术交叉，假如选择的两个个体是，则交叉运算后产生的新个体是:

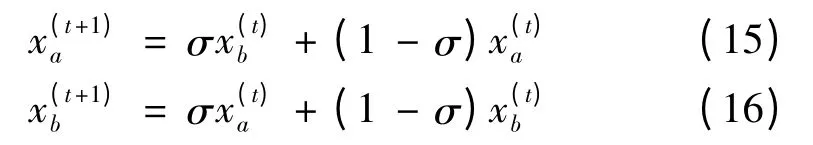
其中σ=l1/l。

(7)终止选择

本文算法中的终止准则采用了预先规定一个最大的迭代次数来终止算法。

4.3 案例分析

经对实际物流情况，工件1～6 的单元内单位物流量的单位距离顺流搬运费用CAp依次为(0.75，0.60，1.00，0.80，0.72，0.50)，逆向搬运费用CBp依次为(1.30，1.25，2.20，1.45，1.50，1.20)，单元间单位物流量的物流搬运费用CXp=20，设备间距D=3.5 m。设定算法最大迭代次数Tmax=400，种群大小sizepop=40，取加速因子c1=c2=2，最大惯性权重ωmax=0.9，最小惯性权重ωmin=0.4，pcmax=0.8，pcmin=0.3，φ=9.9，l=20。采用本文的模型和算法，运用MATLAB 软件编写相应的算法程序并运行，得到其目标函数最优值的收敛情况如图5 所示。从图5 中可以看出，混合粒子群算法大约在第190 代收敛于最优解或近似最优解，目标函数最优值为3 687.8。

根据优化算法结果，将车间内设备分成的5 个制造单元为:制造单元C1{m8，m9，m1，m3，m20};制造单元C2{m15，m7，m11，m18};制造单元C3{m6，m14，m4};制造单元C4{m19，m12，m13，m10};制造单元C5{m5，m17，m16，m2}。按照单元内设备线性布置要求，构建车间的制造单元，并对6 种产品加工过程物流量进行仿真分析，如图6 所示，6 种不同颜色的箭头分别表示6种产品的物流量Wp。

图5 目标函数迭代过程

5 结语

本文研究了制造单元的构建问题，在满足约束条件的情况下，建立了以最小化单元内部及单元之间物流费用为优化目标的数学模型。针对单元构建问题的特殊性，设计了改进粒子群算法，采样两种编码方式实现单元分割点和位置确认，引入交叉操作，并对交叉算子进行非线性设计，使交叉概率随种群中个体适应度值的变化而自适应修正，防止了算法收敛到局部最优解。论文以某企业实际案例为对象进行了单元构建与物流仿真，较好地解决了实际单元构建问题。

［1］Steve Ah kioon，Akif Asil Bulgak，Tolga Bektas.Integrated cellular manufacturing systems design with production planning and dynamic system reconfiguration［J］.European Journal of Operational Research，2007，192 (2):414 -428.

［2］王爱民，丁国智，宁汝新.制造单元快速构建技术研究［J］.北京理工大学学报，2006，26(10):850 -854.

［3］白书清，王爱民，李伯虎.面向应急动员批产的流水式制造单元构建技术［J］.计算机集成制造系统，2008，14(1):64 -73.

［4］王建维.制造单元构建的关键技术研究［D］.大连:大连理工大学，2009.

［5］金哲，宋执环，杨将新.可重构制造系统工艺路线与系统布局设计研究［J］.计算机集成制造系统，2007(1):7 -12.

［6］李淑霞，单鸿波.基于敏捷制造单元的车间动态重构［J］.计算机集成制造系统，2007(3):520 -52.

［7］Jaydeep Balakrishnan，Chun Hung Cheng.Multi -Period planning and uncertainty issues in cellular manufacturing:A review and future directions［J］.European Journal of Operational Research，2007，177:281 -309.

［8］Asokan P，Prabhakaran G，Satheesh G Kumar.Machine-Cell Grouping in Cellular Manufacturing Systems Using Non-traditional Optimization Techniques-A Comparative Study［J］.International Journal of Advanced Manufacturing Technology，2001，18(2):140 -147.

［9］Adil G K，Rajamani D.The tradeoff between intra-cell and inter-cell moves in group technology cell formation［J］.Journal of Manufacturing Systems，2000，19 (5):305 -317.

［10］Sh.Ariafar，N.Ismail.Inter-cell and intra-cell layout design in a cellular manufacturing system［J］.Symposium on Business，Engineeringand Industrial Applications，2011(9)，28 -32.

［11］Nsakanda A L，Diaby M and Price W L.Hybrid genetic approach for solving large-scale capacitated cell formation problems with multiple routings［J］.European Journal of Operational Research，2006，171:1051 -1070.

［12］HU L，YASUDA K.Minimizing material handling cost in cell formation with alternative processing routes by grouping genetic algorithm［J］.International Journal of Production Research，2006，44(11):2133 -2167.