低速风洞收缩段的边界层修正

刘卫红，黄为民

（中国空气动力研究与发展中心 空气动力学国家重点实验室，四川 绵阳 621000）

0 引 言

收缩段是低速风洞的重要部件，它的作用是均匀加速气流，使其达到试验段所需要的流速。收缩段设计时，要保证气流在沿收缩段加速时，洞壁上不出现分离；收缩段出口截面的气流均匀、平行且稳定；收缩段不宜过长。收缩段设计的好坏直接决定了试验段的流场品质。

根据边界层理论，当流场的雷诺数很大时，只在壁面附近一层很薄的流体内部，粘性的作用对流动才是重要的。雷诺数越大，边界层越薄。相对于风洞尺寸来说，收缩段沿程的边界层较薄，通常设计风洞收缩段时是不进行边界层修正的。这一方面是因为收缩段内边界层很薄，二也是因为边界层计算比较繁复。风洞的收缩型面，大多设计为平滑过渡的曲线型面。收缩曲线的设计方法有很多，如 Witozinsky曲线、Batchelor－Shaw曲线、双三次曲线、五次曲线等，具体可参见相关文献［1－3］。

Prandtl［4］认为，考虑边界层发展，收缩段的出口略有扩张可提高试验段流场品质。Borger［5］通过求解无粘势函数方程和边界层积分方程，对收缩段进行了边界层修正并优化了收缩段设计，Wolf［6］、Sanderse［7］等将该方法成功运用于Audi和DNW风洞收缩段设计中，但并未给出通用的边界层厚度分布曲线。

计算流体力学的发展，现在可通过求解雷诺平均NS方程，一并研究主流和边界层内的流动。本文将探讨用CFD方法求解不可压雷诺平均NS方程，研究低速风洞收缩段的边界层发展规律，通过边界层修正来提高试验段流场品质，给出边界层分布的通用曲线，并分析设计参数对边界层的影响。

1 边界层位移厚度

任何实际流体都是有粘性的，粘性对主流的影响是把边界层外边界上的主流向外挤出去一个边界层位移厚度距离δ＊。对于风洞收缩段来说，等于将收缩型面曲线往外移了一个δ＊。因此，在收缩段设计时，先按常规方法设计位流型面曲线，再将各点的位流型面曲线加上当地的边界层位移厚度δ＊，则得到实际收缩段型面坐标。

边界层位移厚度定义为边界层外边界上的主流被向外挤出去的距离。

其中，U为主流速度（主流的速度在物面法向有变化时，U指的是边界层外边界处的流速），vxy 是边界层法向方向坐标点y处沿x方向的流速［8］。

2 研究方法

计算流体力学技术的发展，使得我们可以方便地采用数值方法求解收缩段内流场，并得到高精度的解。对于低速风洞收缩段，本文采用有限体积法，求解轴对称不可压雷诺平均NS方程，对数值模拟结果进行后处理得到沿程的边界层位移厚度来分析沿收缩段壁面边界层的发展规律，并对收缩段型面进行优化设计。

数值模拟时针对轴对称截面收缩段，因轴对称截面收缩段可以采用二维网格进行内流场计算，在现有计算能力下能进行更密的网格划分（边界层内平均有200多个网格点），便于更准确地计算边界层位移厚度，并且为提高模拟精度，采用了双精度数据格式，湍流模型采用SST模型，网格数为1401×501。

2.1 全局坐标系和局部坐标系

建立关于收缩段的全局直角坐标系（x，y），x顺气流方向，y与x垂直，方向竖直向上。

对于收缩段壁面上的点，建立当地的局部直角坐标系（x′，y′），x′沿壁面的切线方向，指向顺气流方向，y′为法线方向，指向收缩段内（图1）。

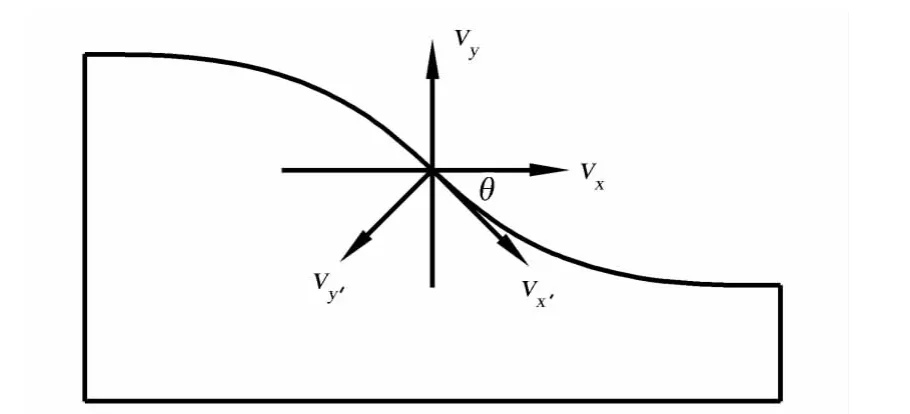
图1 全局坐标系、当地坐标系及速矢图Fig.1 Global and local coordinate system，vector diagram

2.2 速度分解

对于收缩段壁面上的各点，在全局和当地坐标系下进行速度矢量分解，可得速度关系

2.3 边界层位移厚度计算方法

首先选择一典型的收缩型面，并对收缩段内流场进行高精度的数值模拟求解，得到各内点的流动参数。

在收缩段壁面上等距选取了11个站点（图2）。对于每一站点，根据壁面的倾角找到当地的切向和法向方向，建立当地坐标系，并得到当地的切向和法向速度。根据边界层位移厚度计算公式得到各点的边界层位移厚度，再投影到y方向，光滑连接各点的边界层位移厚度即得到收缩段沿程的边界层位移厚度曲线。

图2 典型收缩段壁面上各点的切向和法向方向Fig.2 Tangential and normal direction of point on contraction contour

3 边界层位移厚度的分布规律

选取常用的双三次曲线（xm＝0.5）［9］设计一个收缩比为9的典型轴对称收缩段（case0）。收缩段入口直径9m，出口直径3m，收缩段长度9m。为了统一数据，数值模拟时从收缩段型面入口开始起算。数值模拟时收缩段后加了2倍收缩段长度的平直段来模拟试验段流场，模拟时未考虑试验段扩开角度的影响（图3、图4）。

图3 收缩段型面和边界层位移厚度Fig.3 Contraction contour and boundary displacement thickness

图4 收缩段中心和壁面的压力分布Fig.4 Pressure distribution at the center and contour of contraction

在收缩段入口边界层位移厚度为0之后壁面压力有一个弱的增加，逆压梯度的存在使得边界层位移厚度明显变厚，壁面流动变慢，而中心流速增加；再往下，在壁面转折点前，流体的加速性影响到壁面附近，压力急剧下降，边界层厚度变薄，流动趋于稳定。过了转折点，流体继续加速，在收缩段出口，壁面上有一个小的逆压梯度区，而边界层位移厚度则一直在增加。

收缩段沿程的边界层位移厚度都很薄，最厚处为出口处的13.4mm，与收缩段入口直径之比为0.15%。而且Borgers［5］认为，收缩段出口边界层位移厚度对速度型的影响虽然是明显的，但仍相对较小，即使位移厚度值相差30%仍不会对结果产生明显影响。位移厚度计算时存在一定的人为因素，但并不影响修正后的效果。

4 边界层位移厚度及流场结果分析

4.1 边界层修正前后流场比较

利用分析得到的边界层位移厚度，我们设计了考虑边界层修正后优化的收缩段型面。型面设计方法是按收缩段的进出口截面尺寸扣除位移厚度后进行常规的收缩段型面设计，再加上位移厚度得到新的收缩段型面曲线。

优化设计时比较了两种收缩段型面，一种是严格按照得到的边界层位移厚度，对收缩段整个型面都进行了修正（case1）。另一种是只修正了从收缩段中部最薄边界层以后部分的边界层位移厚度，前半部分的边界层位移厚度采用线性过渡（case2）（图5）。

图5 修正前后收缩段中心和壁面的压力系数分布Fig.5 Pressure coefficient at center and contour for uncorrected and corrected contraction

数值模拟结果表明，边界层修正与否对中心线上的流动没有影响，中心线上的压力系数均呈逐渐下降，不存在逆压梯度。而壁面上压力系数在收缩段进出口附近存在逆压梯度。

对比流场模拟结果，收缩前段是否进行边界层修正对收缩段壁面的压力系数无明显影响。进行边界层修正后，收缩段出口附近的逆压梯度会略增。边界层修正后，收缩段出口截面附近轴心的压力系数减小，速度增大，而壁面的压力系数与未修正时相当，中心和壁面的压力系数差值减小，因而截面速度均匀性会得到显著提高。

收缩段出口截面的速度分布表明（图6），进行边界层修正后，原来速度较低的中心处的速度得到提升，出口截面的速度分布明显比未修正时均匀。

图6 出口截面的速度分布Fig.6 Velocity distribution at contraction exit

对比结果表明（表1），对收缩段型面进行边界层修正后，收缩段出口截面的流场普遍好于未修正时。若只对收缩段后部进行修正，速度场和动压场还可得到提高。经过边界层修正后，动压场系数可下降20%，最大气流偏角可下降35%，收缩段出口截面的速度场得到提高，对下游试验段流场的性能是很有好处的，尤其是对于流场指标要求高的高品质风洞，对收缩段进行边界层修正是一个很好的办法。

表1 轴对称收缩段出口截面75%范围内的速度场、动压场和最大气流偏角Table 1 Velocity，dynamic pressure uniformity and maximum angle at 75%exit area for axi－symmetric contraction

4.2 边界层位移厚度的适用范围

将用双三次曲线得到的边界层位移厚度用到witozinsky曲线设计的收缩段中，收缩段出口速度均匀性也可得到很大提高（图7）。在各种收缩段型面曲线中，Witozinsky曲线因前部收缩剧烈，型面与双三次曲线差别最大，而其它曲线介于两者之间。因此其它曲线采用双三次曲线的边界层位移厚度进行修正的结果应介于二者之间，故对不同收缩型面可用同一的边界层位移厚度进行修正而流场均可得到改进，不必针对每种收缩型面曲线均计算相应的位移厚度，大大节省工作量。

图7 Witozinsky曲线修正后的出口截面速度分布Fig.7 Velocity at exit for Witozinsky contraction

4.3 收缩段口径的影响

比较了收缩段入口尺寸为0.9m，9m，27m三种口径下的收缩段内流场。此时，收缩段采用同样的设计方法，收缩比同样为9，收缩段长径比为1，即收缩段长度分别为0.9m，9m，27m。

图8给出了三种口径下以收缩段入口直径（等于收缩段长度）为参考的无量纲边界层位移厚度值。结果表明，边界层位移厚度受收缩段口径影响较大，尤其是收缩段的前半部分，至收缩段出口处无量纲的边界层位移厚度已基本相同。收缩段口径越小，雷诺数越小，则无量纲的边界层厚度越厚。随着收缩段口径增大，雷诺数变大，则无量纲的边界层厚度也变薄了。

图8 不同收缩段口径下边界层厚度分布Fig.8 Displacement thickness with varying contraction sizes

4.4 收缩比的影响

比较了4、9、16三种常用收缩比下收缩段沿程的边界层位移厚度（图9）。总体来说，收缩比小则边界层位移厚度越小。

4.5 收缩段长度的影响

选择常用收缩段长径比0.8、1.0、1.2进行了边界层位移厚度比较（图10），收缩段长径比通常不会超过这个范围。长径比不同，只对收缩段前半部分的边界层位移厚度影响较明显，而这部分的量值对收缩段出口及试验段流场影响不大，因此，优化修正时可按同一无量纲厚度值进行修正。

图9 不同收缩比下边界层厚度分布Fig.9 Displacement thickness with varying contraction ratio

图10 不同收缩段长度下边界层厚度分布Fig.10 Displacement thickness with varying contraction length

5 矩形截面收缩段的型面修正

以上的讨论分析都是针对轴对称截面收缩段而言的，而实际中还经常用到矩形截面收缩段。

对于矩形截面收缩段，我们可以认为宽度和高度方向的边界层位移厚度是一样的。假设轴对称收缩段半径r截面的边界层位移厚度为，矩形收缩段半宽y，半高z截面的边界层位移厚度为，则位流面积和边界层所占面积存在相似关系

对公式进行整理，得

设计轴对称截面收缩段和矩形截面收缩段的方法是一样的，通常矩形截面的宽高比也近似1，因此有≈，即对矩形截面收缩段进行边界层修正时，可取同口径的轴对称收缩段的边界层位移厚度进行修正。

针对收缩比9的矩形截面收缩段，采用由轴对称收缩段得到的边界层位移厚度进行了收缩段型面优化。再通过求解三维不可压雷诺平均NS方程对修正前后的收缩段内流场进行了数值模拟。模拟结果见表2。模拟结果表明，修正后，动压场和最大气流偏角均有所下降，流场品质得到提高。

图11表明矩形收缩段出口截面速度的最小值在中心处，而最大值出现在顶角处，因此计算得到的速度场值略大，如果不考虑顶角速度高的小范围，则流场的均匀性会得到很大提高。

图11 矩形收缩段出口截面75%范围内速度分布Fig.11 Velocity distribution at 75%exit area for rectangle contraction

因此，对于矩形截面收缩段，也可采用由轴对称截面收缩段得到的边界层位移厚度进行修正来提高流场品质。

6 结 论

本文对低速风洞收缩段边界层位移厚度进行了分析，给出了位移厚度的分布曲线。数值结果证明，进行边界层修正可提高试验段流场品质，并得到如下结论：

（1）对收缩段型面进行边界层修正，可大大提高流场品质。

（2）收缩段的边界层分布呈现先厚再薄再厚规律。

（3）进行边界层修正时，可只对收缩段后半部分的型面进行修正，不影响修正效果。

（4）不同收缩曲线的边界层厚度分布不同，但采用同一个位移厚度分布进行修正，仍可得到满意结果。

（5）轴对称收缩段得到的结果可应用到矩形收缩段上。

［1］刘卫红.轴对称收缩段设计研究［J］.空气动力学学报，1998，16（2）：250－254.

［2］吴宗成，陈晏清，万曦.水洞收缩段流场的数值模拟及优选［J］.北京航空航天大学学报，1998，24（3）：315－318.

［3］周刚，汪家道，陈皓生，等.小型高速水洞收缩段的优化设计［J］.船舶力学，2009，13（4）：513－521.

［4］PRANDTL L.The production of perfect air flows（wind tunnel）［J］.Handbuch Der Experimental Physik Leipzig，1932，4（2）：65－106.

［5］BORGER G G.The optimization of wind tunnel contractions for the subsonic range［R］.NASA TTF－16899，1976.

［6］WOLF T.Design of a variable contraction for a full－scale automotive wind tunnel［R］.AIAA 92－3929，1992.

［7］SANDERSE A.Users－guide for a set of computer programs applicable in design and analysis of contraction contours with varying rectangular cross－section for low－speed wind tunnels［R］.National aerospace laboratory of the Netherlands.Memorandum in－83－009U.April 1983.

［8］徐华舫.空气动力学基础［M］.北京航空学院出版社，1987.

［9］MOREL T.Comprehensive design of axisymmetric wind tunnel contractions［J］.Journal of fluid engineering.ASME Transactions，1975：225－233.

［10］MIKHAIL M N.Optimum design of wind tunnel contractions［J］.AIAA Journal，1979，17（5）：471－477.

［11］CON J Doolan，RICK C Morgans.Numerical evaluation and optimization of low speed wind tunnel contractions［R］.AIAA 2007－3827，2007

［12］王喜魁.风洞高次曲线收缩段壁型及其性能［J］.空气动力学学报，1997，15（2）：251－254.

［13］李国文，徐让书.风洞收缩段曲线气动性能研究［J］.实验流体力学，2009，23（4）：73－76.

［14］张连河，范洁川.三元收缩段优化设计研究［J］.空气动力学学报，2003，21（4）：417－423.

［15］BELL J H，MEHTA R D.Contraction design for small low－speed wind tunnel［R］.NASA－CR－177488，1989.

［16］TAKAGI S，TOKUGAWA N.Laminar－turbulent transition along the contraction nozzle in subsonic flow［R］.AIAA 99－0279，1999.