高超声速飞行体亚密湍流尾迹RCS特性的相似规律研究
2014-04-06于哲峰部绍清石安华梁世昌
于哲峰,部绍清,石安华,梁世昌,马 平,黄 洁
(中国空气动力研究与发展中心,四川 绵阳 621000)
0 引 言
当飞行器以高超声速再入或在临近空间飞行时,周围的空气被急剧压缩、飞行器与空气之间强烈磨擦,表面被加热,产生红外辐射与可见光辐射,弹体表面形成等离子鞘套、飞行器下游形成电离尾迹,极大地改变了飞行器的电磁特性[1-4]。在通常关心的高度80~40km范围内,头身部绕流电离流场一般处于层流状态。而尾迹流场一部分是层流、一部分是湍流。层流的电磁散射一般是镜面散射,其后向散射的比例很小。湍流相对于受照射的电磁波波长,分为过密湍流和亚密湍流,过密湍流是面漫散射,亚密湍流是体散射,亚密湍流的电磁散射的强度通常要比过密湍流大得多。因此,亚密湍流尾迹的雷达特性是防御雷达目标识别的主要研究内容之一,对其进行分析具有重要的实际意义。弹道靶是地面模拟亚密湍流尾迹RCS特性的主力设备,然而利用何种相似规律将弹道靶试验数据外推到真实飞行情况国内外都没有现成的经验可以借鉴。通常亚密湍流尾迹RCS相似规律是在等离子体流场相似的基础上,从等效介电常数相似的思路来推导的,按照这种思路只有进行全尺寸模拟或真实飞行,否则无法将缩比试验数据外推使用,因而寻求通过等效介电常数相似来模拟尾迹的电磁相似是行不通的。为了解决亚密湍流尾迹RCS地面实验数据外推问题,本文开展了探索性研究,从高超声速流场模拟的双缩尺率和亚密湍流尾迹RCS模拟的Born近似出发,推导了真实飞行数据和地面弹道靶试验数据之间亚密湍流尾迹RCS模拟的相似规律。
1 流场结构及流场中等离子体相似
当飞行器以高超声速在大气层中飞行时,高超声速飞行器尾迹处于热/化学非平衡状态,要模拟飞行器的RCS特性首先需要做到等离子体流场相似[5-13]。
目前,在高超声速缩尺试验中通常使用的缩尺规律主要有双缩尺率和三缩尺率,哪一个缩尺规律更适用,主要取决于下面两个电子衰减反应中哪一个占主导地位[2]。

其中双缩尺率是由Birkhoff在1960年提出的,适用于气流中二体化学反应占主导地位时的相似率,这个相似规律通常称为双缩尺律(binary scaling law),其后,Gibson利用数值计算证明,双缩尺律适用于钝头体激波层和激波后的无粘流场。Birkhoff和Gibson的双缩尺率如下:
a.几何相似,且物体的线性尺度有:

b.来流速度V∞相同(马赫数相同),即:

c.来流组份C∞i相同,即:

d.来流温度T∞相同,即:

e.来流密度与物体的线性尺度成反比,即:

其中下标1、2分别表示真实飞行情况和弹道靶试验情况。利用式(1)~(7)可以推导出真实飞行情况和弹道靶试验之间电子密度和碰撞频率的比例关系。对于电子密度:

再考察碰撞频率,对于弱电离气体,电子的平均碰撞频率可以写为:

其中N为所有分子的总数,电子的平均速度¯v为:

因而:

尽管当流场中以三体化学反应为主时,上面的双尺律将被三尺律所代替。但从国外研究结果看,对于80~40km的高弹道部分,双缩尺率大体上适用于大部分再入体流场的电离过程,其中包括有化学非平衡效应的圆球尾迹(包括层流、湍流),细长锥层流边界层、层流尾迹和湍流尾迹。当然双缩尺率的准确度和适用范围还有待进一步确定。图1给出了不同直径圆球尾迹平均电子密度随距离变化结果,可见给定的状态下,圆球尾迹电子密度基本上符合双缩尺率。图2给出细长锥湍流尾迹中双缩尺律的运用范围[1]。

图1 圆球尾迹平均电子密度Fig.1 Wake averange electron density of hypersonic sphere

图2 细长锥湍流尾迹中双缩尺律的运用范围Fig.2 Double scaling law for the turbulent wake of the slender cone
这意味着针对高度80~40km以上的再入弹道,只需模型的飞行速度与再入速度相同(或接近),同时满足上述双尺律,则缩比模型试验就可以对弹头/诱饵流场的流场结构和电子密度进行模拟。目前,在中国空气动力研究与发展中心气动物理靶试验中通常使用的正是这一缩比规律。
2 等效介电常数相似的思路
电磁波与高超声速飞行器尾迹相互作用时的相似规律,不仅要求高超声速飞行器体系与缩尺模型试验体系的几何相似,空气动力学相似,而且要求电磁学相似。文献[9]用量纲分析的π定理方法,从Maxwell方程、Navier-Stokes方程和Boltzmann方程出发导出10个无量纲量相似参数。这些相似参数中有些提出的要求是相互矛盾的,只有真实飞行情况才能满足所有条件。在地面试验中,只能是满足特定条件下的部分相似。
对于完全导体要实现RCS测量的模拟,必须满足模型的几何缩比等于测量波长的缩比,即:

对于亚密湍流尾迹与电磁波(入射雷达波)的相互作用,则没有这种简单的关系。一种相似规律的推导思路是从满足等效介电常数相似出发来进行推导,等离子体的相对介电常数εr是复数,并且有如下形式:
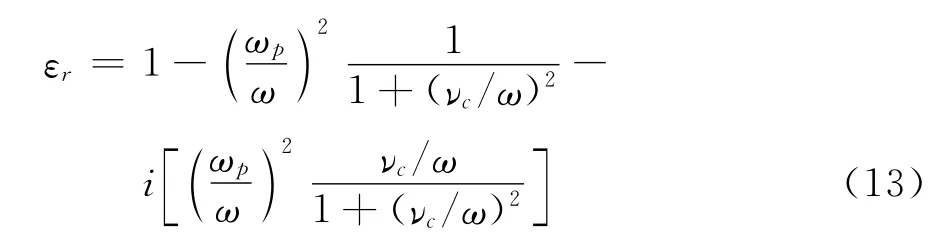
要使两个体系中的等效介电常数相等,则必须有:

对于式(14)需要:

对于式(15)需要:

从式(16)和(17)可以看出,在一般情况下,要使两个体系的等离子体介电常数相等,除两个物体几何相似、物体周围等离子体气动力学相似外,还必须使两个体系的电磁波长比和波长平方比同时等于缩尺因子η,这除了η=1,即全尺寸模拟或真实飞行本身外,别无其它可能。因而寻求通过等效介电常数相似来模拟尾迹的电磁特性相似是行不通的[1-2]。
3 基于Born近似的新思路
寻求通过等效介电常数相似来模拟亚密湍流尾迹的电磁相似是行不通的,为了解决真实飞行情况和弹道靶试验之间亚密湍流尾迹RCS特性相似问题,这里提出了从Born近似出发,直接推导相似规律的思路。
对亚密湍流尾迹进行分析的理论方法主要有Born近似、畸变波Born近似和辐射输运理论等[10]。由Born近似亚密湍流尾迹RCS为:

其中re是典型电子半径,为常数;χ为入射波极化方向和接收机方向之间的夹角;ke=k0-ks为有效波矢,k0和ks分别为入射波和反射波波矢,〈~n2e〉为脉动电子密度均方值,Φ(ke)为谱函数,Shkarofsky给出的各项同性湍流的谱函数可简化为[12]:

式中,μ为能谱函数形状因子,当采用Kolmogorov能谱函数时μ=5/3;ri和r0分别为湍流的内尺度和外尺度;Γ()为Gamma函数。在高超声速条件下,r0沿尾迹从0.1不断增长到约1.0的底部直径,近似分析中常取(其中ReD为以底部半径定义的雷诺数)和r0=0.3倍底部直径的近似关系。当ψ=5/2,ri=0.1r0时,Shkarofsky谱函数变化曲线如图3所示。
图4给出了亚密湍流尾迹RCS特性Born近似计算结果和弹道靶试验结果比较曲线,其中实线为弹道靶试验测量结果,虚线为Born近似计算结果。试验时采用钨铝模型,小钝头锥外形,球头半径为0.87mm,模型长度40.56mm,模型底部直径12.998mm,雷达频率为9.0GHz,雷达波的距离分辨率为2.7个波长,雷达波入射角度为45°。计算时r0=0.3Db,Db为底部直径,ri=0.1r0,脉动电子密度均方值
从图4可以看出,利用Born近似计算得到的亚密湍流尾迹RCS与弹道靶试验测量结果在数量级上非常相符,因此可以把Born近似亚密湍流尾迹RCS的表达式(18)作为推导相似规律的出发点。

图3 Shkarofsky谱函数变化曲线Fig.3 Shkarofsky spectrum

图4 亚密湍流尾迹一维距离像Fig.4 Experimental and simulating one dimentional RCS image of underdense turbulent wake

将式(20)和(21)代入(19)有:
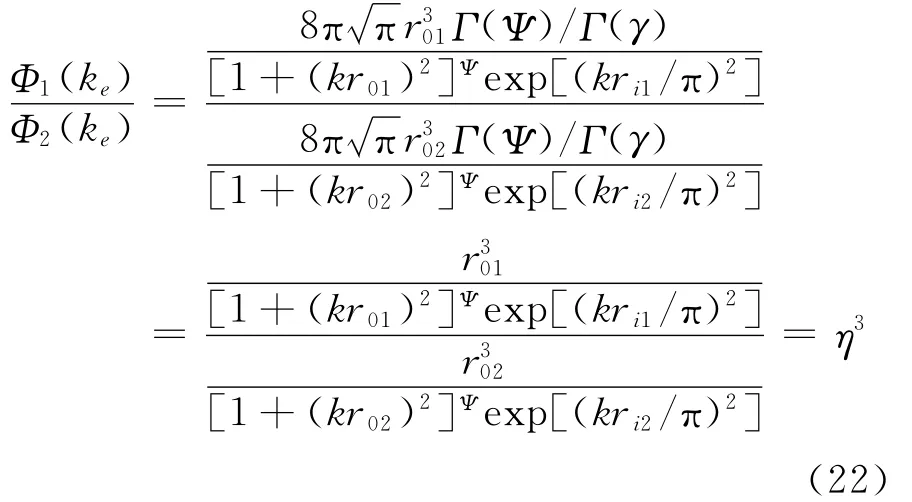
由体积积分公式有:

将式(20)~(23)代入式(18)得:


图5 由相似规律得到的实际飞行器亚密湍动尾迹RCSFig.5 One dimentional RCS image of underdense turbulent wake deduced by the scaling law
从式(24)可知,若真实飞行器与弹道靶试验模型之间有 D1/D2=η,V∞1=V∞2,ρ∞1/ρ∞2=1/η,ω1/ω2=1/η,即流场模拟按照双缩尺率缩比,若弹道靶雷达频率为9.0GHz,则对应真实飞行条件下飞行器测量雷达波频率180MHz并且有雷达散射截面缩比关系为σ1/σ2=η4=504,即67.95dB。也就是说弹道靶试验频率为9.0GHz雷达的测量结果加上67.95dB就是真实飞行条件下频率为180MHz雷达的测量结果(图5)。
4 结 论
本文从高超声速流场模拟的双缩尺率和亚密湍流尾迹RCS模拟的Born近似出发,推导出真实飞行条件下和地面弹道靶试验之间亚密湍流尾迹RCS模拟的一种相似规律,推导结果显示当D1/D2=η,V∞1=V∞2,ρ∞1/ρ∞2=1/η,ω1/ω2=λ2/λ1=1/η时,雷达散射截面服从σ1/σ2=η4的相似规律。使用该相似规律的一个好处是只需要在弹道靶试验中测量雷达散射截面,不需要测量尾迹的电子数密度分布和湍流的内外尺度。当然,使用该相似规律有很多假设和前提,比如说双缩尺率和Born近似,这些假设和前提是否成立或可以在什么条件下使用还需要进一步地探讨。通常认为尾迹中离解反应(1)占主导地位时尾迹流场满足双缩尺率。而Born近似则要求尾迹高亚密为临界电子密度)和弱起伏此时可以只考虑电子对入射波的一次散射。
应该看到,高超声速飞行器亚密湍流尾迹RCS特性相似规律研究是一个非常困难的问题,国内尚未专门开展过这方面的研究,而国外公开发表的文献中也没有现成的公式可以借鉴。本文相似规律的推导是在很多假设和前提下进行的,是否能够真正实用还需要更多的理论研究和试验验证。
[1]LE Jialing,GAO Tiesuo,ZENG Xuejun.Reentry physics[M].Beijing:National Defence Industry Press,2005.(in Chinese)乐嘉陵,高铁锁,曾学军.再入物理[M].北京:国防工业出版社,2005.
[2]ZHANG Zhicheng.Aerophysics[M].Beijing:National Defence Industry Press,2013.(in Chinese)张志成.气动物理学[M].北京:国防工业出版社,2013.
[3]ZHANG Zhicheng,GAO Tiesuo,DONG Weizhong.Study on modeling of re-entry vehicle signatures[J].Journal of Experiments in Fluid Machanics,2007,21(2):7-12.(in Chinese)张志成,高铁锁,董维中.再入飞行器目标特性建模研究[J].实验流体力学,2007,21(2):7-12.
[4]RICHARD A H.The application of light gas gun facilities for hyper-velocity aerophysics research[R].AIAA 92-3998.
[5]BEISER A,RABB B.Hydromagnetic and plasma scaling laws[J].Phys.Fluids,1961,4:177-181.
[6]LEES L.Hypersonicwakes and trails[J].AIAA Journal,1964,2:417-428.
[7]BIRKHOFF G.Hydrodynamics,A study in logic fat and similitude[M].Princeton University Press,Princeton,1960.
[8]PRIMICH R I,STEIBERG M.Aboard survey of freeflight range measurements from the flow about spheres and cones[R].AD-427050,1963.
[9]AKIRA I.Wave propagation and scattering in random media[M].Academic Press,1978.
[10]MENKES J.Scattering ofwaves by an underdense turbulent plasma[J].AIAA Journal,1964,2(6):826-832.
[11]SHKAROFSKY I P.Generalizedturbulence space-correlation and wave number spectrum-function pair[J].Can.J.Phys.,1968,46(19):213-253.
[12]BISBING P E.Development of acomputer model for scattering of electromagnetic waves by a turbulent wake[R].AD-032662,1976.
[13]HAYAMI R A.Theapplication of light gas gun facilities for hypervelocity aerophysics research[R].AIAA-923998,1992.
[14]ZENG Xuejun,YU Zhefeng,BU Shaoqing,et al.Research on the RCS of hypervelocity model and its plasma sheath[J].Acta Aerodynamica Sinica,2010,28(6):645-649.(in Chinese)曾学军,于哲峰,部绍清,等.超高速模型及其等离子体鞘套RCS特性研究[J].空气动力学学报,2010,28(6):645-649.
[15]LIANG Shichang,YU Zhefeng,ZHANG Zhicheng.Research on the RCS characteristics of blunt-cone with slots and plasma sheath[J].Journal of Experiments in Fluid Mechanics,2013,27(2):20-24.(in Chinese)梁世昌,于哲峰,张志成.开槽钝锥体及等离子体鞘套的RCS特性研究[J].实验流体力学,2013,27(2):20-24.
[16]ZHANG Hanxin.The similarity law for eal gas flow[J].Acta Aerodynamica Sinica,1990,8(1):1-8.(in Chinese)张涵信.真实气体流动的相似规律[J].空气动力学学报,1990,8(1):1-8.
[17]YU Ming.The study of turbulent characteristics of reentry wake[D].Mechanical Institute of the Chinese A-cademy of Science,2000.(in Chinese)于明.再入尾迹电磁特性的湍流效应研究[D].中国科学院力学研究所.2000.
