可压缩混合层的涡结构演化与流质混合
2014-04-06沈孟育
周 强,何 枫,沈孟育
(清华大学 航天航空学院,北京 100084)
0 引 言
可压缩平面自由剪切层,是指两股速度不等的平行气流在自由空间相互混合,其初始混合面为平面。这种流动是可压缩湍流研究的典型问题,也是超燃冲压发动机内基本流动的结构。超声速平面混合层厚度增长率远低于亚声速混合层和不可压混合层的增长率,所以提高超声速平面混合层增长率、增强燃料混合是超燃冲压发动机需要解决的关键技术之一。
Barre[2]等利用纹影技术对超声速混合层进行了实验研究,发现当对流马赫数Mc=0.62时,超声速混合层的发展对初始条件十分敏感,但充分发展段湍流的这种依赖性相对较弱,湍流应力的大小和各向异性特征受到可压缩性的影响。Clemens & Mungal[3]利用纹影技术、平面激光诱导荧光技术和米散射技术研究了Mc为0.28、0.62和0.79的超声速平面混合层中大尺度涡结构及其卷吸能力,给出了不同对流马赫数下大尺度结构的空间存在形状。熊红亮、崔尔杰[4]利用纹影成像技术测出了可压缩混合层的厚度增长率曲线,纹影照片显示随着对流马赫数增加,可压缩混合层厚度增长率显著降低,涡卷起现象延迟,结果还表明适当增加分隔板厚度有利于平板尾缘可压缩混合层中的涡提前卷起,有利于促进混合。Zhao[5]等使用高分辨率的NPLS方法对超声速混合层进行了流动显示并进行了湍流分形结构研究,结果显示在转捩区域分形维数随着湍流强度的增强而增长,在自相似区域分形维数基本维持不变。
由于超声速实验观测的难度,定量实验信息仍然非常有限,在分析解读所获取的实验结果上,缺乏足够的理论依据,使得现有的实验结果所能展示的定量流动信息非常有限,数值模拟便成为重要的研究手段之一。
在早期的研究中,数值模拟一般都是针对时间发展混合层[6-10]。在低对流马赫数的情况下时间发展的结果是真实的三维空间发展混合层结果的良好近似,但在高对流马赫数时二者存在有较大差别[11-12]。因此高对流马赫数三维空间发展混合层的精细结构的数值模拟就显得特别重要。可压缩混合层空间发展模式的数值模拟,无论是直接数值模拟(DNS)还是大涡模拟(LES)都得到了混合层发展早期阶段的信息[13-17],例如都捕捉到初期的Λ涡和马蹄涡的出现,随对流马赫数的增高动量厚度沿空间增长发展变缓慢等等物理现象。但对混合层涡结构的中后期湍流发展的研究不多,关注不同尺度的涡结构对流质混合作用的研究也不多,还缺乏足够全面的信息来加深对可压缩湍流的认识,这在很大程度上是因为受到计算规模或经费的限制,而这方面的研究对认识可压缩混合层发展的物理机制,以及提出新的增混举措或思路有着重要的意义。
本文采用约4亿规模的网格以及作者自己构造的七阶精度广义紧致格式离散对流项,用显式八阶精度的中心格式离散粘性项,数值求解了非定常三维可压缩Navier-Stokes(NS)方程,直接数值模拟了对流马赫数为0.7的超声速可压缩混合层的空间发展流动,获得了自初始流动失稳直至充分发展湍流流动结构的精细演化历程,并着重于研究结构的演化对混合层中流质混合的作用。
1 可压缩混合层直接数值模拟方法简述
以高速侧来流参数作为相应的特征参数和进口处无扰动速度剖面的涡量厚度为特征长度,对非定常三维可压缩NS方程及其定解条件和完全气体状态方程进行无量纲化。无量纲化后的NS方程组可参见文献[6]。
对流项先经Steger-Warming矢通量分裂技术[18]分裂成非正和非负两部分,然后对正负通量均采用作者提出的七阶广义紧致格式进行离散[19]。该紧致格式可表达如下:
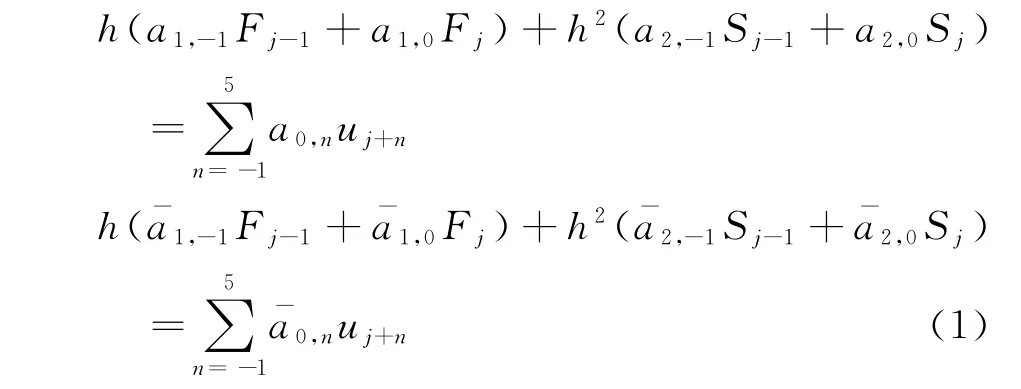
其中,u为求导函数(此处即为分裂后的通量),F为一阶导数,S为二阶导数,h为网格间距。格式系数am,n和的具体数值以及非周期边界的匹配方法可参见文献[19]。值得注意的是,格式中出现了二阶导数。Fourier分析表明二阶导数的存在使得一阶导数获得了更好的分辨率性质[19]。
在我国西南地区的深山野林里,生长着一种草本植物,它开着白色的小花,虽然看上去清新可爱,却也没什么特别之处。但是,如果下雨之后你再来看,便会发现原先白色的小花变得晶莹剔透,就像精心雕琢后的精美艺术品。你知道这种神奇植物的名字吗?
对NS方程中的粘性项,本文采用普通显式八阶精度的中心格式进行离散。时间积分采用八步四阶具有强稳定保持性质的Runge-Kutta格式[20]。同时求解的还有无量纲被动标量质量分数输运方程,该方程的具体表达可参见文献[6]。
初始流向速度场采用上下来流定解条件下的可压缩边界层方程的数值解[21],横向速度假设为0;初始温度剖面由Crocco-Busemann关系求得,普朗特数设为0.75,混合层上下侧密度相同。
入口边界在可压缩边界层的数值解基础上添加扰动。若加入随机扰动,则流动要经历很长的空间线性稳定发展后,最不稳定波才成为主导,随后流动呈非线性发展,这将耗费很多计算时间。为减少DNS的计算成本,使流动较快进入转捩阶段,本文在入口处直接添加最不稳定波形式的扰动[21]。扰动波由一对振幅相同方向相反的最不稳定斜波组成,该斜波的具体形式可参见文献[21-22]。
在流向超声速出口边界处无需设定边界条件,其上流动参数直接由内点外插得到;展向采用周期边界条件;法向上下两侧均采用无反射边界条件[6]。
为显示转捩后湍流流场的空间演化,直到湍流自相似区,计算域流向(以x表示)必须足够长;混合层初始混合平面以y=0表示,故y为流动的法线方向;计算域的展向(以z表示)的宽度应根据湍流脉动相关量是否能够在展向半个宽度内衰减为0来设定。
本文中空间发展混合层的DNS计算域选为长方形[0,L1]×[-100,100]×[0,L2],其中L1、L2分别为流向x和展向z混合层线性稳定性分析下各自最不稳定波波长的54倍和2倍。参照Pantano &Sarkar[23]和 Wu & Moin[24]所做 DNS的经验设定网格密度,网格数为4160×351×256。所有计算在中科院计算机网络信息中心进行。
2 可压缩混合层的涡结构演化与流质混合
本文中DNS的对象为:对流马赫数为0.7,上下来流马赫数分别为2.8和1.4,普朗特数为0.75,以入口处上下自由来流速度差和动量厚度为特征量定义的雷诺数为80。Ho &Huerre[25]研究表明上述定义的雷诺数大于50时,不稳定波的发展和涡结构的演化基本不受雷诺数的影响。
计算保证不同流向x处的平均流向速度剖面沿法向的分布进入自相似区,流向脉动速度的展向无量纲能谱中高波数对应的小尺度(Kolmogorov尺度)湍流的粘性子区的能谱,呈现出Heisenberg[26]通过能量级串理论给出的-7次方律,说明DNS的计算网格密度足以解析粘性子区的小尺度流动细节。通过监测湍动能输运方程残量的大小,发现数值残量相对各输运项数值大小是可以忽略的,即数值耗散远小于物理耗散,表明物理粘性在计算结果中可得到正确的反映。关于本文计算结果的可靠性验证的详细阐述,见文献[22]。
展现涡结构的形态有多种方法,本文采用旋转强度(速度梯度的共轭复特征值的虚部的平方)为0.025等值面显示不同尺度的涡结构形态。
可压缩混合层三维结构从早期不稳定波到涡结构破碎的演化全过程已在文献[22]中有详细描述。为了研究涡结构演化对流质混合的作用,本文对涡结构演化过程将做简单概述。
图1(a)和图1(b)显示了不同视角下涡结构展现的形态,对应流向坐标为x≈0~250,图中从蓝到红不同色度反映的是结构在空间法向相对位置的由低到高,由此可以清晰地展示结构在法向方向上的扩张演化。

图1 流动结构演化(旋转强度为0.025等值面)Fig.1 Vortex structures(isosurfaces of swirl strength with value of 0.025)
在入口处直接加入较强幅度的最不稳定波扰动后,混合层离入口仅一个基频波长就形成了强剪切层(x≈0~11),之后在混合层上下迅速卷起Λ斜波(x≈11~45)。在Λ斜波交接处不连续,生长着类似帽子的薄壳结构,在剪切作用下这个交接处开始向混合层外侧伸展,并演化为马蹄涡的形态(x≈50~80),生长在Λ斜波的两腿上,而仔细观察Λ斜波结构上开始附着稍小的结构。马蹄涡头部在剪切力的作用下开始失去稳定,演变成颈部有半环形项链涡的结构,在位于入口的8倍基频波长处(x≈88~140)形成复杂的团花形态,而斜波的形态已经不再清晰了;在12倍流向基频波长处,团花结构被拉伸并开始破碎,出现大量的各种方位的细管状结构;约在x≈450之后流动进入湍流自相似区,充斥着更加细碎的小涡结构,并且这些细碎的小结构管条状结构整体以一种大的拟序结构向下游迁移。关于涡结构演化的三维视图和湍流自相似区的小涡形态可参看文献[22]。
图1(a)至图1(b)还清晰地展现了混合层上下侧不对称的发展演化。下侧涡结构演化略早于上侧,下侧的涡花结构产生较早,在较强的剪切下很快破碎,而上侧的涡花结构维持过程相对长些。不对称发展的根本原因在于涡结构的抬起使得涡结构的行进速度受到了主流的影响。关于该点的详细解释见参考文献[22]的图9以及与图9相关的论述。结构这种上下不对称的发展使得流质的混合也向下侧偏移发展。
式(2)为沿流向动量厚度计算公式[27],其中¯ρ为展向平均的雷诺时均统计值;ρ1为初始来流高速侧密度。采用式(2),可以得动量厚度沿流向的变化曲线(文献[22]中的图14b)。

从动量厚度曲线可以看出在流向初始阶段(x<200),动量厚度呈现快速增长阶段,如果对应图1可知,这一阶段是从Λ涡发展到团花涡结构丰富的演化过程阶段;x>200团花失稳破碎,流动进入转捩。在进入充分发展湍流阶段,动量厚度的曲线趋于线性增长时期,转捩后的动量厚度增长率基本不变。x<200是大尺度结构演化阶段,是在主流的强剪切作用下、混合层快速吸收主流动量和能量的发展阶段,这个过程越早发生或者延长这个阶段的生存期,会促使混合层动量厚度曲线在x>200的后阶段向上平移,虽然在充分发展阶段的沿流向的增长率未必提高,但最终动量厚度的绝对值会提高。
在混合层发展的不同空间阶段,对应不同尺度结构,这些形态各异的结构对流质混合的作用也是不同的。图2~图7展示了在不同涡结构的旋转卷吸作用下,由被动标量质量分数显示的混合效果,白色为0是下侧来流初始质量分数,黑色为1是上侧来流初始质量分数,同时也给出了相应的涡量云图。
图2(a)为混合层初始发展起来的Λ涡结构,如果对流场信息做平行流动方向的投影z=8.83铅垂切面A,该投影面恰好穿过Λ涡头部,如图2(a)所示。图2(b)和图2(c)为该切面上的展向涡量分布云图和质量分数分布云图。Λ涡头部几乎是展向方向的强旋转促进了流体混合,并使混合层界面沿流向产生很大的波动,由于混合层法向上下各发展的Λ涡略有所不同,在y<0低速侧的Λ涡头部具有更集中和强度更大的负展向涡量。

图2 Λ涡在展向z=8.83切面上的展向涡量云图和被动标量云图Fig.2 Vorticity contours and passive scalar contours corresponding to vortexΛat the plane z=8.83
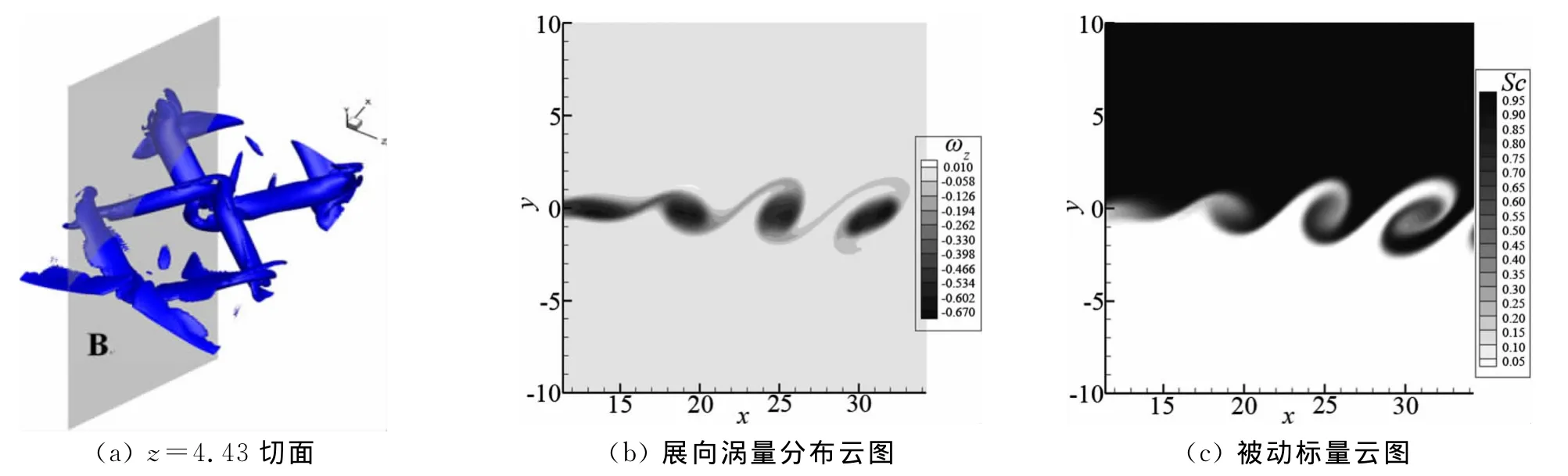
图3 Λ涡在展向z=4.43切面上的展向涡量云图和被动标量云图Fig.3 Vorticity contours and passive scalar contours corresponding toΛvortex at the plane z=4.43

图4 Λ涡在流向x=25.3切面上的流向涡量云图和被动标量云图Fig.4 Vorticity contours and passive scalar contours corresponding toΛvortex at the plane x=25.3

图5 马蹄涡作用下的混合被动标量云图Fig.5 Passive scalar contours corresponding to horseshoe shaped vortex at the plane z=8.83、17.0respectively

图6 团花结构对应的混合被动标量云图Fig.6 Passive scalar contours corresponding to flower-ball shaped vortex at the plane z=4.43、13respectively

图7 充分发展小尺度湍流结构作用下的混合被动标量云图,z=8.83和z=13切面Fig.7 Passive scalar contours corresponding to full development flow at the plane z=8.83、13respectively
如果对流场信息做平行流动方向的投影z=4.43铅垂切面B,如图3(a)所示,切面错过了Λ涡头部,由图3(b)和图3(c)可以看到该切面上的展向涡量分布云图和质量分数分布云图与图2(b)、图2(c)是不同的。图3(b)中Λ涡腿之间的涡量,使得切面上呈现出类似不可压混合层的涡卷序列,而实际是不同空间位置的Λ涡腿诱导出的展向涡量分布。从图3(c)被动标量质量分数分布可以看出,其涡腿对上下流质混合是有一定的卷吸作用,但相对Λ涡交接的头部而言(图2c),图3(c)对应的混合层直观可视厚度还是相对小的。结合图2(c)和图3(c)表明混合层沿展向z的混合效果是不相同不均匀的,混合接触界面是三维波动形式。
如果做图4(a)所示的x=25.3切面C,该切面是切在了同一个涡的双腿间。可以看出,在主流强剪切作用下,涡的双腿被拉伸并变成扁椭圆形,特别是这个涡涡腿之间的相对旋转造成涡腿间的射流,主要使得混合层低速侧的流质向高速侧喷注(或高速侧向低速侧喷注),相对旋转的两涡腿内混合均匀。如图4(c)所示混合层界面产生间歇性的大波动,为后续混合发展奠定了基础。
随着Λ涡头部向混合层外侧伸展,涡的形态演化为马蹄涡。图5显示了主要演化出的马蹄涡和展向z=8.83和z=17.0切面上的被动标量的云图。马蹄涡的宽头部的强旋转使得对应的混合层界面的局部区域可视混合厚度相对较大。这时混合层的界面开始破碎形成更多的接触面,上下流体开始在涡的作用下进行混合。
图6是马蹄涡结构头部演化成团花结构时期在不同的展向切面上对应的混合状态被动标量云图,以及如图7所示进入充分发展湍流阶段不同展向切面上的混合状态。可以看到在湍流的小尺度结构作用下混合趋于均匀并沿展向混合状态基本相同,这个时期对应x>200,结合动量厚度曲线(文献[22]的图14(b))可知混合层厚度沿流向的增长变得很缓慢。
如果将被动标量0<Sc<1显示的质量分数的混合,看成是定性的可视混合层厚度,由图8不同展向切面上的可视混合可以看出,混合层向低速侧偏移发展,与图1(b)显示的低速侧的大结构发展先于高速侧相呼应。最终x>450充分发展湍流阶段的混合基本上是在x=100~200间的可视混合厚度量级基础上进行的,这个阶段可视混合在法向上的扩展并不大,小尺度的湍流结构混合耗散的使得流质混合趋于均匀,由此也可见先期大尺度结构的发展使得混合层从主流获取动量和能量,主宰着混合层可视厚度的发展量级,而充分发展阶段对混合的主要贡献是使这个厚度量级内的流质混合均匀化。

图8 不同z展向切面上的可视混合效果Fig.8 Visual mixing layer shown by passive scalar contours at the z-plane
3 结 论
采用DNS的方法研究对流马赫数为0.7的可压缩混合层问题,得到了自混合层失稳涡开始卷起直至充分发展湍流的整个流动结构演化的历程。混合层在最不稳定波主导下开始失稳,旋转强度等值面显示下的流动结构开始具有初始的涡卷起结构,随后形成Λ涡。Λ涡涡腿的交接处会在剪切作用下发展为马蹄涡,马蹄涡是生长在Λ涡涡腿上的,并且法向方向生长沿流向倾斜演化。马蹄涡又在剪切作用下其头部演化更加复杂的团花形态,而Λ涡涡腿形态上开始包含着稍小尺度的结构。团花结构最终在剪切的作用下失稳破碎,混合层流场中的结构逐渐趋于管状的涡结构形态。在充分发展阶段,混合层中充斥着更加细碎的小尺度三维管状涡结构。这些位于不同阶段的各种涡结构形态,对混合层的接触面和流质混合产生了不同的作用,特别是初期演化的Λ涡结构、马蹄涡、团花等大尺度结构从主流获得的能量和质量,使得混合层的界面在法向和展向产生很大波动,使混合层的动量厚度沿流向急剧增长,而在充分发展湍流阶段,细碎涡结构作用下的均匀混合主要是在大尺度营造的可视混合层厚度量级的基础上进行的。
[1]LELE S K.Compressibility effects on turbulence[J].Annual Review of Fluid Mechanics,1994,26:211-254.
[2]BARRE S,QUINE C,DUSSAUGE J P.Compressibility effects on the structure of supersonic mixing layers:experimental results[J].Journal of Fluid Mechanics,1994,259:47-78.
[3]CLEMENS N T,MUNGAL M G.Large-scale structure and entrainment in the supersonic mixing layer[J].Journal of Fluid Mechanics,1995,284:171-216.
[4]XIONG H L,CUI E J.Studies on flow dynamics of compressible mixing layer and mixing enhancement[A].Proceedings of frontier research symposium on aerodynamics[C],2003:491-497.(in Chinese)熊红亮,崔尔杰.可压缩混合层流动特性与增混措施研究[A].空气动力学前沿研究学术研讨会论文集[C],2003:491-497.
[5]ZHAO Y X,YI S H,TIAN L F,et al.The fractal measurement of experimental images of supersonic turbulent mixing layer[J].Science in China Series G:Physics Mechanics and Astronomy,2008,51(N8):1134-1143.
[6]SANDHAM N D,REYNOLDS W C.Three dimensional simulations of large eddies in the compressible mixing layer[J].Journal of Fluid Mechanics,1991,224:133-58.
[7]VREMAN B,KUERTEN H,GEURTS B.Shocks in direct numerical simulation of the confined three-dimensional mixing layer[J].Physics of Fluids,1995,7(9):2105-2107.
[8]FU D X,MA Y W.Direct numerical simulation of three-dimensional temporally evolving compressible mixing layer[J].ACTA Mechanica Sinica,1998,30(2):129-137.(in Chinese)傅德薰,马延文.时间发展平面混合流的三维演化[J].力学学报,1998,30(2):129-137.
[9]FU D X,MA Y W,ZHANG L B.Direct numerical simulation of transition and turbulence in compressible mixing layer[J].Science in China(Series A),2000,43(4):421-429.
[10]KOURTA A,SAUVAGE R.Computation of supersonic mixing layers[J].Physics of Fluids,2002,14(11):3790-3797.
[11]ROGERS M M,MOSER R D.The three-dimensional evolution of a plane mixing layer Part 1.the Kelvin-Helmholtz rollup[R].NASA TM-103856,N92-11303,1992.
[12]LI Q,ZHANG H X,GAO S C.Numerical simulations on supersonic shear layer flow[J].ACTA Aerodynamica Sinica,2000,18(S1):67-77.(in Chinese)李沁,张涵信,高树椿.关于超声速剪切流动的数值模拟[J].空气动力学学报,2000,18(S1):67-77.
[13]LI Q B.Numerical study of compressible mixing layer with BGK scheme[D].Beijing:Tsinghua University,2002.(in Chinese)李启兵.应用BGK格式对可压缩混合层的数值研究[D].[博士学位论文].北京:清华大学,2002.
[14]FU S,LI Q B.Numerical simulation of compressible mixing layers[J].Int.J.Heat Fluid Flow,2006,27:895-901.
[15]PAN H L,MA H D,WANG Q.Transition coherent structures and shocklets in 3-D spatial developing mixing layers at high convective Mach numbers[J].ACTA Aerodynamica Sinica,2008,26(3):275-281.(in Chinese)潘宏禄,马汉东,王强.高对流Mach数三维混合层转捩特性分析及小激波结构模拟[J].空气动力学学报,2008,26(3):275-281.
[16]LI Q,LUO J R,ZHANG H X.Studies on several issues of three-dimensional temporally and spatially developing mixing layer[J].Physics of Gases-Theory and Applications,2009,4(1):45-57.(in Chinese)李沁,罗俊荣,张涵信.三维时间和空间发展混合层若干问题研究[J].气体物理-理论与应用,2009,4(1):45-57.
[17]ZHOU Q,HE F,SHEN M Y.The evolution of three-dimensional temporally evolving plane mixing layers under strong vortex disturbances[J].Tsinghua Science and Technology,2009,14(S2):17-21.
[18]STEGER J L,WARMING R F.Flux vector splitting of the inviscid gasdynamic equations with application to finite difference methods[J].Journal of Computational Physics,1981,40:263-293.
[19]ZHOU Q,YAO Z H,HE F,et al.A new family of high-order compact upwind difference schemes with good spectral resolu-tion[J].Journal of Computational Physics,2007,227(2):1306-1339.
[20]SPITERI R J,RUUTH S J.Non-linear evolution using optimal fourth-order strong-stability-preserving Runge-Kutta methods[J].Math.Comput.Simul.,2003,62:125-135.
[21]SANDHAM N D,REYNOLDS W C.Compressible mixing layer:linear theory and direct simulation[J].AIAA J.,1990,28:618-624.
[22]ZHOU Q,HE F,SHEN M Y.Direct numerical simulation of a spatially developing compressible plane mixing layer:flow structures and mean flow properties[J].Journal of Fluid Mechanics,2012,711:437-468.
[23]PANTANO C,SARKAR S.A study of compressibility effects in the high-speed turbulent shear layer using direct simulation[J].Journal of Fluid Mechanics,2002,451:329-371.
[24]WU X H,MOIN P.Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer[J].Journal of Fluid Mechanics,2009,630:5-41.
[25]HO C M,HUERRE P.Perturbed free shear layers[J].Annual Review of Fluid Mechanics,1984,16:365-424.
[26]HEISENBERG W.Zur statistischen theorie der turbulenz[J].Z.Phys.,1948,124:628-657.
[27]BROWAND F K,LATIGO B O.Growth of the two-dimensional mixing layer from a turbulent and nonturbulent boundary layer[J].Physics of Fluids,1979,22(6):1011-1019.
