关于模椭圆曲线上的格点计算

董祥南

(江西师范大学数学与信息科学学院，江西 南昌330022)

0 引言

设a，b，c∈Z，形如y2=x3+ax2+bx+c的曲线，称为模椭圆曲线，这是一类非常重要的代数曲线，其在数论计算中有很重要的地位和作用，特别是曲线上的格点(即满足曲线方程的点P(x，y)的2个坐标分量都是整数的点)的计算。本文计算了几条模椭圆曲线，找出了这些模椭圆曲线上的所有格点。

1 引理及主要定理的证明

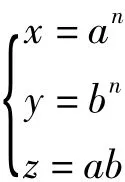
定理1:模椭圆曲线y2+y=x3上有且仅有2个格点(x，y)=(0，0)。

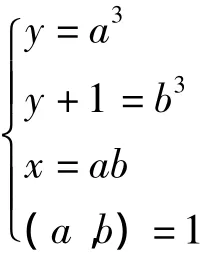
推论1:模椭圆曲线y2－y=x3上有且仅有2个格点(x，y)=(0，0)，(0，1)。

定理2:模椭圆曲线y2=x3+x上有且仅有一个格点(x，y)=(0，0)。

推论2:模椭圆曲线y2=x3－x上有且仅有3个格点(x，y)=(0，0)，(1，0)，(－1，0)。

定理3:设素数p满足p≡3(mod 4)，则模椭圆曲线py2=x3+x2+x+1上没有满足x≠－1 (mod p)的格点。

证明:用反证法证。假设(x，y)是定理3中曲线上的满足x≠－1(mod p)的格点，则满足曲线方程py2=x3+x2+x+1=(x+1)(x2+1)，注意到(x+1，x2+1)=1或2，于是就有:

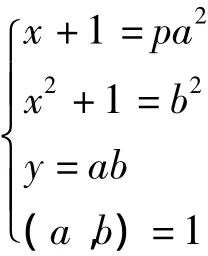
综合上面的各种情况，即知定理3的结论成立。

定理4:设素数p≡±3(mod 8)，则模椭圆曲线py2=x3+x2－2x－2上没有格点。

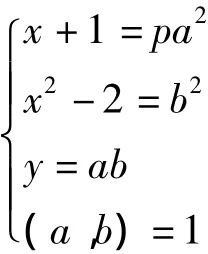
引理2［3］:设D是一个非平方数的正整数，则方程x2－Dy4=1(x，y∈N)至多有2组解。

定理5:设p≡5(mod 12)是素数，则模椭圆曲线y2=px(x2+3)上至多存在2组正整数解。

证明:设(m，n)是模椭圆曲线y2=px(x2+3)上的整数点，则有:n2=pm(m2+3)，于是就有p| n，故可令n=pk，则pk2=m(m2+3)，注意到:(m，m2+3)=(m，3)=1或3。

情形1:如果(m，m2+3)=1，则由引理1可得

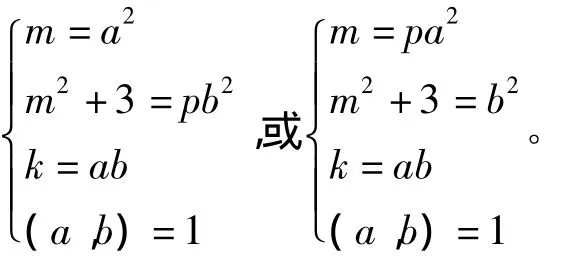
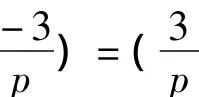
情形2:如果(m，m2+3)=3，则3|m，故可令m=3r，则由于p是素数，就有3|k，令k=3s，就得到ps2=r(3r2+1)，由于(r，3r2+1)=(r，1)=1，因此由引理1就有:

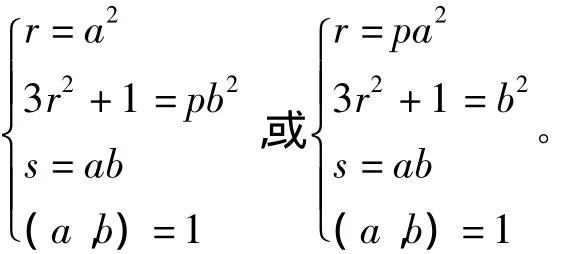
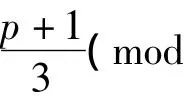
综合上述各种情况就得到:模椭圆曲线y2= px(x2+3)上至多存在2组正整数解。

［1］ 闵嗣鹤，严士健.初等数论(第2版)［M］.北京:高等教育出版社，1982.

［2］ 华罗庚.数论导引［M］.北京:科学出版社，1957.

［3］ Walsh P G.A note on a theorem of Ljunggrem and the Diophantine equation x2－kxy2+y4=1，4［J］.Anal.Math.(Basel)，1999，73(1):119－125.