关于Smarandache双阶乘函数与伪Smarandache函数的混合均值

鲁伟阳，高 丽，郝虹斐

(延安大学数学与计算机科学学院，陕西 延安716000)

1 引言及结论

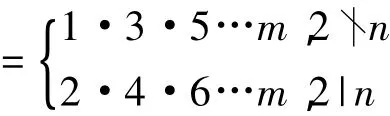
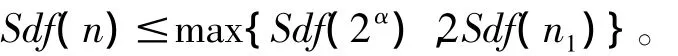
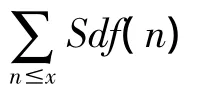
著名的伪Smarandache函数Z(n)定义为最小的正整数m使得n≤m(m+1)/2，即Z(n)= min{m∶m∈N，n≤m(m+1)/2}。关于函数Z (n)的初等性质，许多学者进行了研究，并获得了不少有意义的结果［4～7］。例如:Yuanbing Lou［6］研究了一个包含伪Smarandache函数的均值问题，得到了一个渐近式:

Lin Cheng［7］也讨论了一个包含伪Smarandache函数的均值，得到渐近式:

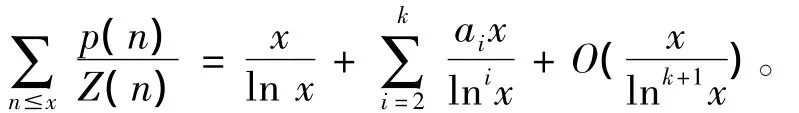
吴启斌［8］讨论了复合函数S(Z(n))的均值，得到较强的渐近公式

其中，ci(i=1，2，…，k)为可计算的常数，S(n)为著名的Smarandache函数。

刘华［9］讨论了复合函数SL(Z(n))的均值，同样得到一个较强的渐近式

其中，bi(i=1，2，…，k)为可计算的常数，SL(n)为著名的F Smarandache LCM函数。

本文主要在上述文献的基础上，利用初等方法和解析方法研究了复合函数Sdf(Z(n))的均值问题，并得到一个较强的渐近公式。下面给出本文的主要结论。

定理:设k≥2是一个给定的整数，则对于任意的实数x＞1，有渐近公式

其中，ai(i=1，2，…，k)是可计算的常数。特别地，当k=1时，有下面简单的推论成立。

推论:对于任意的实数x＞1，有渐近公式

2 相关引理

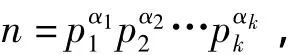
(2)若2|n，且n=2αn1，其中α，n是正整数，21，则有Sdf(n)≤max{Sdf(2α)，2Sdf(n1)}。

引理2［3］:对任意的正整数n，若P(n)是n的最大素因子，那么有如下结论成立:

3 定理的证明

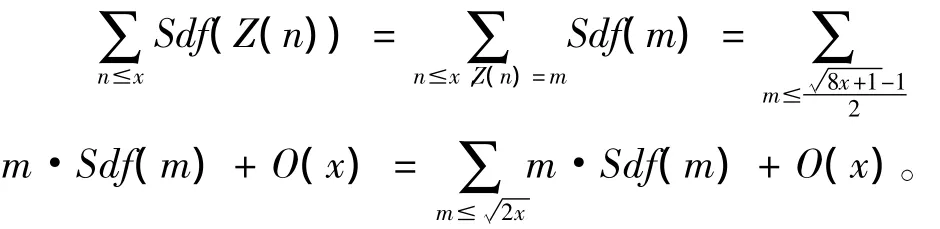
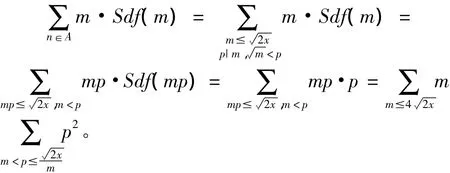
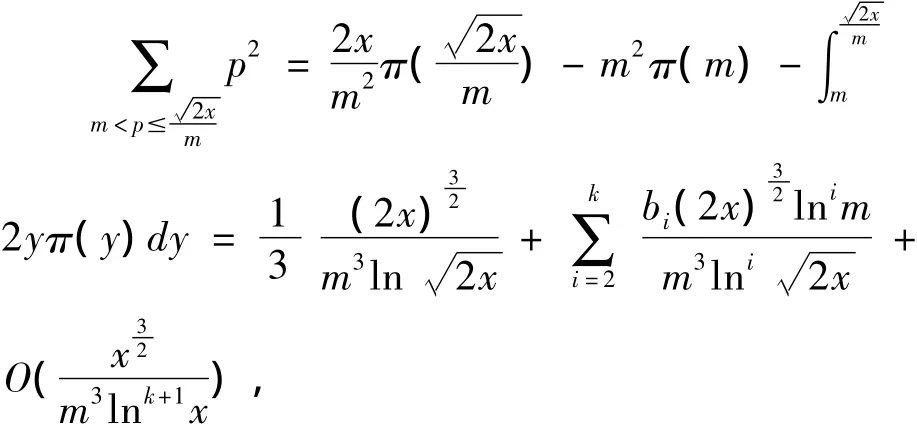
其中，ai(i=1，2，…，k)是可计算的常数。

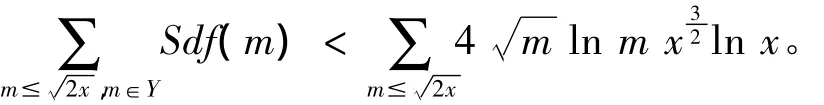
因此有

综上可知，

其中，ai(i=1，2，…，k)是可计算的常数。证毕。

有趣的发现，如果外函数具有与Smarandache函数S(n)类似的性质，则其与伪Smarandache函数的复合函数均值的渐近公式是相同的。

［1］ Le M H.A conjecture concerning the smarandache dual function［J］.Smarandache Notions Journal，2004，14 (3):153－155.

［2］ 沈 虹.一个新的数论函数及其它的均值分布［J］.纯粹数学与应用数学，2007，23(2):235－238.

［3］ 樊旭辉，闫欣荣.关于Smarandache双阶乘sdf(n)函数的均值估计［J］.空军工程大学学报(自然科学版)，2013，14(4):88－90.

［4］ Kashihara Kenichiro.Comments and Topics on Smarandache Notions and Problems［M］.USA:Erhus University Press，1996.

［5］ Majumdar A A K.A note on the Pseudo-Smarandache function［J］.Scientia Magna，2006，(3):1－25.

［6］ Lou Y B.On the pseudo Smarandache function［J］.Scientia Magna，2007，(4):48－50.

［7］ Lin Cheng.On the mean value of the Pseudo-Smarandache function［J］.Scientia Magna，2007，(3):97－100.

［8］ 吴启斌.一个包含Smarandache函数的复合函数［J］.纯粹数学与应用数学，2007，23(4):463－466.

［9］ 刘 华，吕松涛.一个包含F Smarandache函数的复合函数［J］.江西科学，2009，27(3):325－327.

［10］ Le M H.On the Smarandache double factorial function［J］.Smarandache Notions Journal，2002，13:209－228.

［11］ Jozsef Sandor.On certain inequalities involving the Smarandache function［J］.Scientia Magna，2006，2 (3):78－80.

［12］ Tom M.Apostol.Introduction to analytic number theory［M］.New York:Spring-Verlag，1976.

［13］ 潘承洞，潘承彪.素数定理的初等证明［M］.上海:上海科学技术出版社，1988.