求解HJB方程的两类迭代法研究

杨建鹅，黄晓梅

(江西师范大学数学与信息科学学院，江西 南昌330022)

0 引言

HJB方程最早出现于用动态规划解最优控制问题，之后在科学、工程、经济领域中得到广泛应用［1～5］。本文考虑如下HJB方程:

其中，Ω是R2上的有界区域，∂Ω为Ω充分光滑的边界，Fj为光滑函数，Lj为如下二阶椭圆算子:

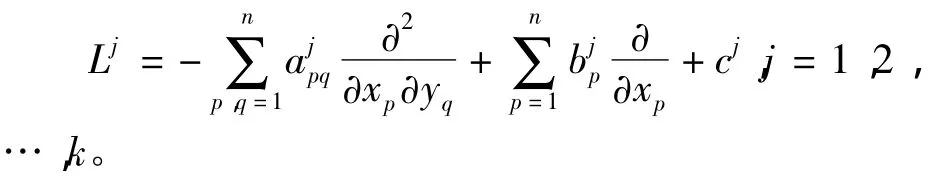
对方程(1)采用有限差分法或有限元方法进行离散，可以得到如下离散格式的 HJB方程［6～8］:

其中，Aj∈Rn×n，Fj∈Rn，j=1，2，…，k。方程(2)是非光滑的方程组。

条件A:Aj=()，j=1，2，…，k，是L矩阵(即≤0，p≠q，p，q=1，2，…，n)且Aj，j =1，2，…，k，是严格对角占优的。

目前人们提出了很多迭代算法解离散HJB方程［8～14］。本文基于上下解策略，提出两类新的迭代法求解方程(2)，该算法的特点是简单易行。下面给出上解集和下解集的定义。

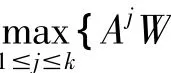
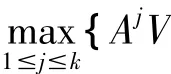
1 算法

下面给出求解离散HJB方程的两类算法。

1.1 算法1(Jacobi型迭代算法)

第1步:取ε＞0，初始值U0∈S1，m∶=0;

第2步:计算

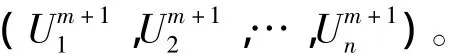
第3步:如果‖Um+1－Um‖＜ε，则停止计算;否则令m∶=m+1，转第2步。

1.2 算法2(Gauss-Seidel型迭代算法)

第1步:取ε＞0，初始值U0∈S1，m∶=0;

第2步:计算

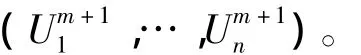
第3步:‖Um+1－Um‖＜ε，则停止计算;否则令m∶=m+1，转第2步。

注:当k=1时，算法1、算法2分别为求解线性方程组的Jacobi迭代法和Gauss-Seidel迭代法。若U0∈S0，算法1和算法2也是收敛的。

2 算法的收敛性

这一节，给出算法1和算法2的收敛性定理。在证明算法1和算法2的收敛性定理之前，先给出几个重要的引理。

引理1［9］:设系数矩阵Aj，j=1，…，k，满足条件A或条件B，那么对任意的sl(l=1，…，n)，矩阵A(s1，…，sn)为M矩阵。

引理2:设系数矩阵Aj，j=1，…，k，满足条件A或条件B，且{Um}是算法1产生的迭代序列，那么{Um}是一个单调下降的上解序列，即{Um}⊆S1且Um+1≤Um，m=0，1，2，…。

证明:既然U0∈S1，由归纳法原理，只需要证明对任意m，若Um∈S1，则Um+1∈S1，且Um+1≤Um。

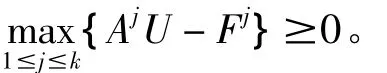
由算法1及上述不等式知

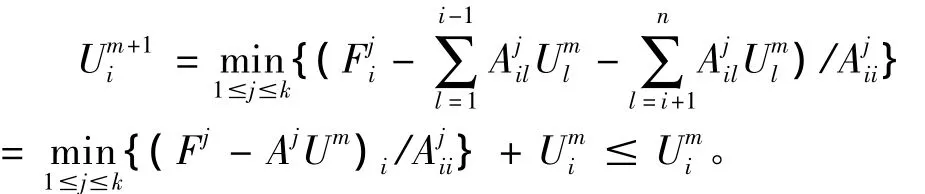
从而Um+1≤Um。

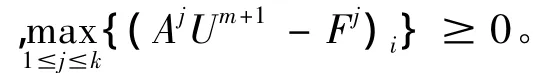
由算法1的第2步知:

那么存在某个ji(1≤ji≤k)，使得

也就是说，

而Um+1≤Um，故

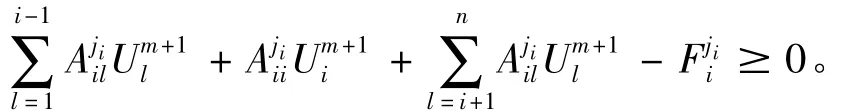
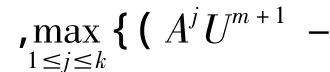
定理1:设系数矩阵Aj，j=1…，k，满足条件A或条件B，且{Um}是算法1产生的迭代序列，那么{Um}单调收敛于方程(2)的解。

证明:由引理2知:Um+1≤Um，m=0，1，2，…。下面证明{Um}有下界。

对任意的m=0，1，…，都存在一组(s1，…，sn)，使得－Fj}≥0。

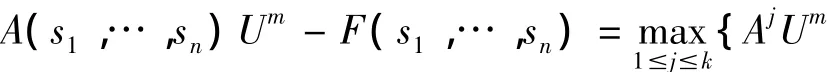
既然A(s1，…，sn)为M矩阵，那么方程A(s1，…，sn)W－F(s1，…，sn)=0存在唯一解。记为W (s1，…，sn)。由于

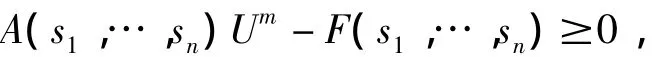
所以，Um≥W(s1，…，sn)。令

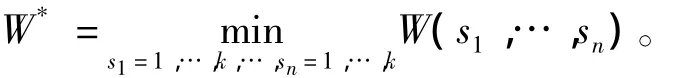
又由于

在上式中令m→∞，则

从而

因此U*是方程(2)的解。

引理3:设系数矩阵Aj，j=1，…k，满足条件A或条件B，且{Um}是算法2产生的迭代序列，那么{Um}是一个单调下降的上解序列，即{Um}⊆S1且Um+1≤Um，m=0，1，2，…。

证明:由算法2可知，U0∈S1，利用归纳法原理，只需要证明对任意m，若Um∈S1，则Um+1∈S1，且Um+1≤Um。假设Um∈S1，下面证明Um+1≤Um。由算法2知，

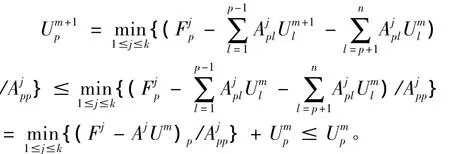
根据归纳法原理知，Um+1≤Um。

下面证明Um+1∈S1。对任意的i=1，2，…，n，

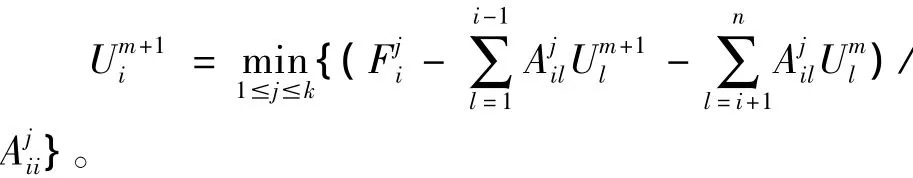
定理2:设系数矩阵Aj，j=1，…，k，满足条件A或条件B，且{Um}算法2产生的迭代序列，那么{Um}单调收敛于方程(2)的解。

证明:证明过程类似定理1的过程，此处省略。

注:在算法1和算法2中若取初始值为下解，则算法产生的迭代序列单调上升收敛于方程(2)的解。

3 数值实验

考虑下列问题:

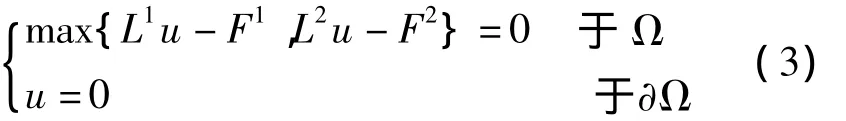
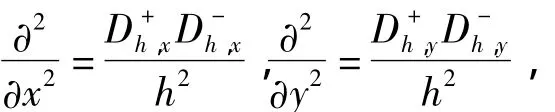
其中，

在数值实验中，取迭代终止准则ε=10－6，初始值为U0=(A1)－1F1。表1和表2分别给出网格点(0.5，0.2)处的迭代值，迭代次数及前后2次迭代的误差，其中网格点(0.5，0.2)处的精确值为0.587 78，误差取为‖Um+1－Um‖∞。

(1)算法1终止时的迭代次数为51次，花费时间为0.781 00 s。

表1 Jacobi型迭代法解HJB方程所得的结果

(2)算法2终止时的迭代次数为27，花费时间为0.343 00 s。

表2 Gauss-Seidel型迭代法解HJB方程所得的结果

通过比较表1与表2，发现取同一个初值时，Gauss-Seidel型迭代算法比Jacobi型迭代算法迭代次数少将近一半，所花时间也减少了一半左右，所得到的解也更接近精确解。因而Gauss-Seidel型迭代算法比Jacobi型迭代算法收敛速度更快。

［1］ Bellman R.Dynamic Programming［M］.New Jersey: Princeton Univ Press，1957.

［2］ Stanislaw S.Hamilton-Jacobi-Bellman equations and dynamic programming for power-maximizing relaxation of radiation［J］.International Journal of Heat and Mass Transfer，2007，50:2714－2732.

［3］ Bellman R.Adaptive Control Processes:A Guided Tour［M］.New Jersey:Princeton University Press，1961:1－42.

［4］ Bensoussan A，Lions J L.Impulse Control and Quasi-Variational Inequalities［M］.Paris:Gauthier Villars，1984:1－31.

［5］ Fleming W H，Rishel R.Deterministic and Stochastic Optimal Control［M］.Berlin:Springer，1975:1－27.

［6］ Boulbrachene M，Haiour M.The finite element approximation of Hamilton-Jacobi-Bellman equations［J］.Comput.Math.Appl.，2001，14:993－1007.

［7］ Lions P L，Mercier B.Approximation numerique des equations de Hamilton-Jacobi-Bellman［J］.RAIRO Numerique Analyse，1980，14:369－393.

［8］ Sun M.Domain decomposition method for solving HJB equations［J］.Numer.Funct.Anal.Optim.，1993，14: 145－166.

［9］ Zhou S Z，Zhan W P.A new domain decomposition method for an HJB equatoin［J］.J.Comput.Appl.Math.，2003，159:195－204.

［10］ Hoppe R H W.Multigrid methods for Hamilton-Jacobi-Belman equations［J］.Numer.Math.，1986，49:239－254.

［11］ Huang C S，Wang S，Teo K S.On application of an alternating direction method to HJB equations［J］.J.Comput.Appl.Math.，2004，166:153－166.

［12］ Sun M.Alternating direction algorithms for solving HJB equations［J］.Appl.Math.Optim.，1996，34:267－277.

［13］ Zhou S Z，Chen G H.A monotone iterative algorithm for a discrete HJB equation(in Chinese)［J］.Math.Appl.2005，18:639－643.

［14］Xu H R，Sun Z，Xie S L.An iterative algorithm for solving a kind of discrete HJB equation with M-functions［J］.Appl.Math.Lett.，2011，24(3):279－282.