基于QAR模型的地方政府性债务规模上限研究——以重庆市为例<br/>

基于QAR模型的地方政府性债务规模上限研究——以重庆市为例

2014-04-03郭红玉詹佳华

金融理论与实践 2014年11期

关键词：负债率插值法可持续性

郭红玉，许争，詹佳华

（1.对外经济贸易大学金融学院，北京 100029；2.中信银行总行营业部，北京 100032）

基于QAR模型的地方政府性债务规模上限研究
——以重庆市为例

郭红玉1，许争1，詹佳华2

（1.对外经济贸易大学金融学院，北京 100029；2.中信银行总行营业部，北京 100032）

实证结果显示：一方面，重庆市政府性债务负担较重，未来债务风险较大；另一方面，重庆市政府性债务关键分位数相对较低，重庆市债务承受能力较弱。通过上述研究，为我国地方政府性债务风险管理提供可借鉴的思路与方法，对于中央与地方政府合理管控地方政府性债务规模有重要意义。

地方政府性债务；QAR模型；债务上限；债务风险

一、引言

地方政府性债务资金在支持地方基础设施建设，应对国际金融危机，保持经济平稳增长等方面发挥了重要作用。根据国家审计署2013年7月进行的我国政府性债务的审计结果显示：截至2013年6月底，地方政府负有偿还责任的债务108859.17亿元，政府或有负债（政府负有担保责任的债务和政府可能承担一定救助责任的债务）70049.49亿元①数据来源：审计署2013年12月30日公告《全国政府性债务审计结果》http://www.audit.gov.cn/n1992130/n1992150/n1992500/n3432077.files/n3432112.pdf。。虽然审计署在综合评估了负债率、政府外债与GDP（国内生产总值）的比率、债务率和逾期债务率等指标后，认为我国政府性债务（包括中央政府债务和地方政府债务）风险总体上可控，但是地方政府性债务仍然暴露出诸多问题，特别是地方政府负有偿还责任的债务增长较快、部分地方政府和行业债务负担较重等不容忽视。随着我国经济进入中高速增长阶段，地方政府在地方经济建设中仍会发挥不可替代的重要作用，如地方基础设施建设、民生工程建设等领域。在此背景下，研究地方政府性债务可持续性问题是极为必要的，地方政府性债务是否具有可持续性已成为评估地方政府性债务风险的关键。

国外学者对于政府债务可持续性的研究起步较早，这一概念已经广泛应用于评估和预警政府债务风险。特别是在欧洲主权债务危机之后，主权债务可持续性研究已成为国外学者关注的热点问题。相比之下，中国地方政府性债务可持续性的研究还比较少。国内大多研究集中在中央政府债务可持续性上（周子康、金江明，2003[1]；涂立桥，2005[2]；陈建奇，2006[3]；杨宇、沈坤荣，2010；吴许璐、王亚芬，2010[4]；李辉文，2013[5]），对地方政府性债务的关注度不够，且研究方法也多以定性分析和指标分析为主（洪源、李礼，2006[6]；刘立峰，2009[7]；孙玉亮，2011；睢党臣、李盼，2013；季军，2013）。但是，由于公共债务（包括地方政府性债务）一般具有非线性特征，这会导致债务数据在长期看似平稳和可持续的，而在某个短时期内可能不可持续。债务指标如债务率、负债率和偿债率等不能够反映这一现象；STAR模型、Markov—switching模型和TAR模型等虽然能够识别债务时间序列的这一特征，但都不能确定具体是哪个时间段债务具有不可持续性，即债务超出了其上限，因此，这些模型都不能够及时识别债务风险，也就不能起到债务风险预警的作用。相比而言，在主权债务上限评估中得到广泛使用的分位数自回归(Quantile Autoregressive，QAR)模型不但能够识别债务率数据非线性特征，还能够依据模型的分位数特征找出时间序列的非平稳点，也就是债务不可持续的时间段，从而对债务风险进行合理预警。

本文在债务可持续理论的基础上，采用QAR模型构建地方政府性债务上限，来分析国内地方政府性债务可持续问题，打破了传统的地方政府性债务可持续性的分析思路，对于中央和地方政府评估债务风险有开创性意义。

二、基于QAR的地方政府债务上限模型构建

QAR模型在国债预警方面有着广泛的应用。该模型首先由Koenker和Bassett(1978)[8]提出，Lima etal.（2008）成功将其应用到主权债务可持续性和债务上限的研究中，在Hamilton和Flavin（1986）与Wilcox（1989）债务可持续性研究基础上，运用该模型得到时变的主权债务上限。与传统时间序列回归模型要求时间序列满足平稳性相比，QAR模型引入了不对称性，即样本中既有平稳序列，也有非平稳序列。这使得QAR模型能够很好地处理非对称冲击。实际上，由于负债状况是动态变化的，即使某段时期内负债水平不可持续，但经过一段时间调整负债水平可能变为可持续的。因此QAR模型的特殊性质使其适合描述负债水平的变化，能够有效区分债务率波动路径上的平稳点和非平稳点，进而识别政府债务风险。考虑到QAR模型建立在债务可持续性理论基础之上，因此，本文首先对债务可持续理论进行简要回顾。

（一）政府债务的可持续性理论

债务可持续性理论认为，政府债务风险取决于政府债务的可持续性（包括短期和长期），可持续就不存在风险，反之则存在风险。债务可持续是指借债主体的长期经济水平能负担其债务。从量化角度来看，该理论认为债务可持续性的充要条件是折现后的负债率是平稳且均值为零的序列。而债务上限就是满足债务可持续性的最高负债率，即在满足贴现后的负债率平稳且趋于零条件下的最高负债率。

政府债务的可持续性理论具体推导过程如下。政府预算约束（名义变量）为：

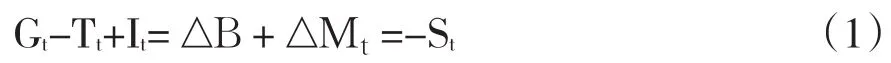
其中，G表示政府支出，T表示税收，B表示政府在t期的政府债务，M是基础货币，S是总预算盈余，I是指政府债务的利息。将公式（1）除以名义GDP，那么以占GDP比重形式表示的预算约束为：

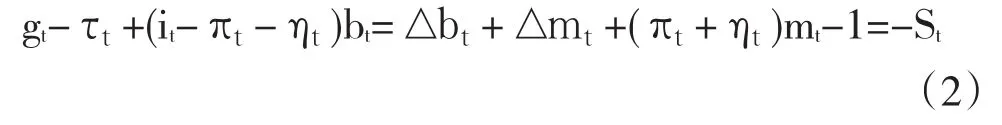
变量g，τ，m和s分别表示各变量与名义GDP的比重，πt=(Pt-Pt-1)/Pt-1，ηt=(Yt-Yt-1)，P和Y分别代表价格水平和实际GDP。因此，式（2）变形为：

其中，dt=gt- τt- △mt-(πt+ ηt)mt-1，dt表示政府财政赤字占名义GDP的比重，ρt=it-πt-ηt，表示经实际产出增长调整的实际利率。为了检验未来折现的财政盈余总额能否补偿当期债务与GDP比率，式（3）需要求解。如果对于所有t都有 ρt＜0，那么式（3）将会是一个平稳的差分方程，可以通过向后求解得出方程的解。这就意味着在任何有限的债务赤字率dt序列中债务与GDP比率bt仍然是有限的。需要注意的是，当ρ和d是常数时，b在稳定状态下的值为-d/ρ。当 ρt＞0，在dt＞0的条件下，债务与GDP比率将最终无解，需要极力避免出现这种情况。

此外，t+1期的预算约束可以表达为：

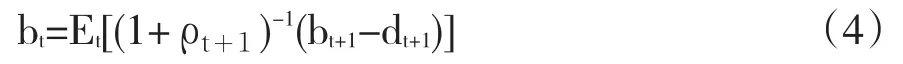
bt在t期是已知的，其期望值是依赖于t期可以获得的信息。将式（4）向前推导可以得到n期的跨期预算约束：

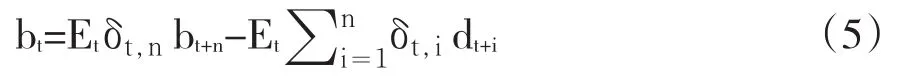
在标准情况下，令a0=1，并且定义Xt=atbt和Zt=at-dt，分别表示折现后的债务与GDP比率和债务赤字与GDP比率。这样，式（5）所代表的现值条件下的借贷约束可以写成式（6）或者式（7）。

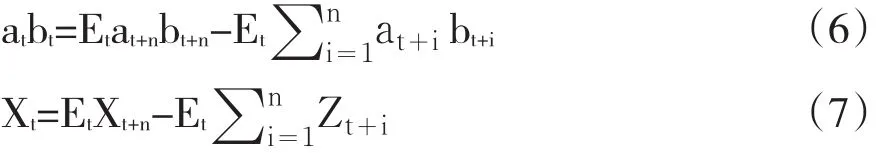
单期预算约束已由式（3）给出，其在折现条件下的形式可以由下式给出：

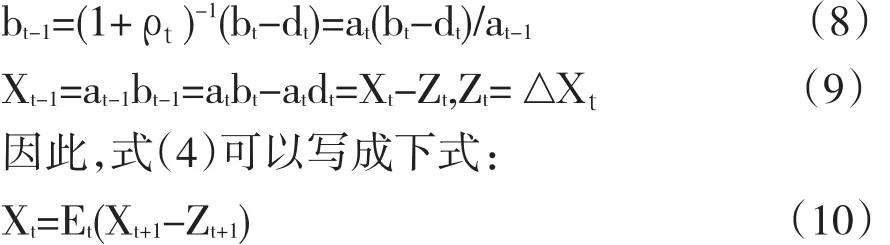
债务可持续性理论认为债务可持续的充要条件是随着n趋向于无穷，折现的债务与GDP比率的期望趋向于0，用公式表示就是limn→∞Et(Xt+n)=0。满足这样的条件，说明当期债务与GDP比率将会被现在和将来折现后的财政盈余（以占GDP比重的形式表示）所抵消，从而不会存在债务不可持续危机。因此，政府预算约束的现值形式可以表述为：

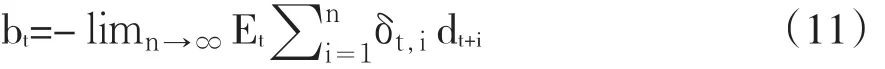
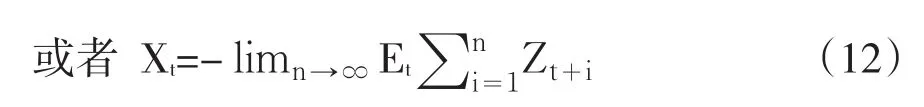
跨期预算约束（12）成立的充要条件是折现后的债务与GDP比率（Xt）是平稳且均值为0的过程。这样，如果当前财政政策（如借债）是不可持续的，那么未来财政政策就必须做出调整，以保证政府债务长期可持续性。

（二）分位数自回归模型设定

QAR模型的具体设定如下：设{yt}为贴现后的负债率，假定{Ut}是均值为0、标准差为1的独立同分布标准正态分布变量，且ai(Ut)，i=0，1，…，p是单调的随机变量，可以定义p阶自回归过程如下：

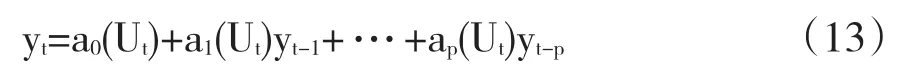
类似于AR(p)模型，但是其系数αi为服从(0，1)均匀分布的随机变量Ut的函数。这种设定使得QAR模型与传统的AR模型相比更适合于描述负债水平。由于QAR模型的系数是随机变量，其序列中可能有平稳的部分，也可能有不平稳的部分。而传统的AR模型的系数为常数，其序列只能是全部平稳或者全部不平稳。由于负债状况是能动态调整的，即使某段时间内负债水平不可持续，经过经济调整负债水平可能变为可持续的。因此QAR模型的特殊性质使其适合描述负债水平的变化。

设τ是Ut的分位数，则yt的条件分位数形式为式（14）。定义关键分位数 τcrit，它表示满足如条件下的最大分位数。设 τcrit为满足的最大的 τ，即满足平稳性条件的最大分位数，则称为关键分位数(CriticalQuantile)。而yt的关键条件分位数(Critical Conditional Quantile)就是 Qyt(τcrit|Ft-1)。

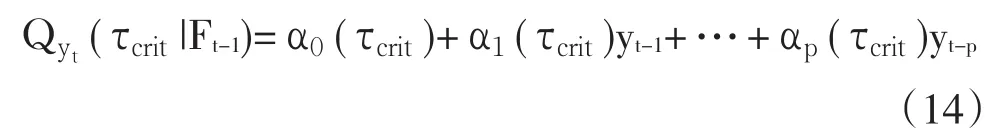
该式表示yt在τ=τcrit时第τ阶条件分位数的函数值。那么有如下定理：在QAR(p)模型中，当函数yt在时间γ内是单位根过程，那么yt的关键条件分位数一定会低于yt本身，也就是 Qyt(τt|Ft-1)＜yt，∀t∈ γ ，γ⊂Ω，Ω表示总体的样本。因此，如果yt的实际观测值高于模型对应的分位数，那么yt序列是单位根过程；相反，如果yt的实际观测值低于模型对应的分位数，那么yt序列平稳。

应用于债务问题的QAR模型中，分位数选择越大，负债率越高。使模型平稳的最大分位数就是关键分位数，在符合最大负债率的同时，也满足了模型的平稳性。债务上限Dt等于当债务满足可持续性条件时的关键分位数，即Dt=Qyt(τcrit|Ft-1)。也就是说，当{yt}协方差平稳且均值为零时，Qyt就是债务上限。当yt＜Qyt时，序列部分平稳，即债务是可持续的；当yt＞Qyt时，序列部分不平稳，即债务是不可持续的。因此，将债务上限和实际债务率进行比较，从而识别债务的可持续性风险——当实际债务率高于关键分位数时，地方政府债务是不可持续的。

三、地方政府性债务上限的实证结果与经济解释

（一）研究样本概述

选择重庆市作为研究样本展开实证分析，数据时间窗口是2004年1季度到2013年2季度，数据主要来源于中国统计年鉴、重庆市统计年鉴、wind数据库。同时，由于有部分数据无法从统计年鉴中直接得到，故而需采取下文提到的插值法获得。这里地方政府性债务不仅包括直接偿还的债务，还包括或有负债。参考国家审计署在计算或有负债时所用的方法，本文赋予政府负有担保责任的债务和政府可能承担一定救助责任的债务的权重系数为19.13%和14.64%，因此，地方政府性债务总额=政府负有偿还责任的债务+政府负有担保责任的债务×19.13%+政府可能承担一定救助责任的债务×14.64%。

（二）模型变量的设定

对于模型变量的选取问题，负债率是最重要的变量，因为QAR模型是对负债率建立分位数自回归模型，按照本文对地方政府性债务的界定与Lima et al（.2008）的实证研究，模型负债率的代理变量等于地方政府性债务总额与地方名义GDP比率。

由于QAR模型的理论基础是债务可持续性理论，债务可持续的充分必要条件是贴现后的负债率平稳且均值为0，因此，基于QAR的债务上限模型应该使用贴现后的负债率。由上文可知折现因子αt=，α0=1，1+ ρt=(1+it)/(1+ πt)(1+ ηt)，也就是说负债的贴现率需要已知同期利率、价格水平增长率以及实际产出增长率。利率水平采用同业拆借利率及shibor数据，由于shibor从2007年开始形成报价并对外公布，因此以2007年为分界线，2007年之前的利率水平采用银行间市场的回购利率，之后采用shibor；价格水平增长率则为通胀率，通常用CPI增长率来体现；而实际产出增长率则用实际GDP增长率表示。

（三）研究样本的提取和插值处理

1.研究样本的提取

模型中提取的样本指标包括：负债率、实际GDP增长率、价格水平增长率和同期利率。其中负债率选用地方政府负债率作为代理变量，包括负有偿还责任的债务和或有债务；价格水平增长率选用消费价格指数（CPI）的增长率为代理变量；同期利率选用同业拆借利率和银行间回购利率作为代理变量。

2.插值处理

大部分变量仅在较短时间内有季度数据，其余时间内都是只有年度数据，特别是政府债务数据，往往具有模糊性和难以获得的特点。因此如果使用已有的季度数据，样本量可能不足，样本覆盖的时间范围可能过短；使用已有的年度数据虽然能够解决上述问题，但是较低的频率包含的信息可能不足，导致估计效果较差。为了解决这个问题，对于季度数据不可知的年份，本文使用插值法得到季度数据。插值法的基本思想就是基于已知的样本找到季度数据的规律，通过插值得到不可知的季度数据。①插值法分为移动平均插值法和同比插值法。一般来说，同比插值法所得数据的标准差低于移动平均插值法，而且移动平均插值法要求已知较多的季度数据，而同比插值法对于季度数据样本的依赖较低，因此，同比插值法比移动平均插值法的适用效果更佳。同比插值法的特点是假设同一年里不同季度的同比增长率相同。比如2010年第一季度负债率相对于2009年第一季度负债率的增长率与2010年第二季度的相对于2009年第二季度的增长率相同，等同于2010年年度负债率相对于2009年年度负债率的增长率。

（四）重庆市债务上限估计与预测

1.模型滞后项阶数选择

在模型滞后阶的选择上，借鉴Kolmogorov—Smirnov检验，利用LR统计量来确定滞后阶数，初步得到模型的滞后项p=pmax=3。那么，QAR模型就是：

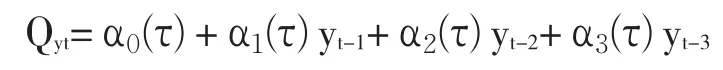
模型中的分位数τ∈Γ=[0.1,0.9]，其中分位数的步长设置为0.005。然后需检验模型中第三阶的系数 α3(τ)是否相关，其原假设为：H0∶α3(τ)=0，τ∈ Γ 。

从表1可知，自变量yt-3的系数无法拒绝原假设，即模型不包括yt-3项。因此继续检验二阶变量是否相关，依然考虑如下原假设：H0∶α2(τ)=0，τ∈ Γ 。结果显示拒绝二阶检验的原假设，因此模型的最佳滞后阶数是二阶。

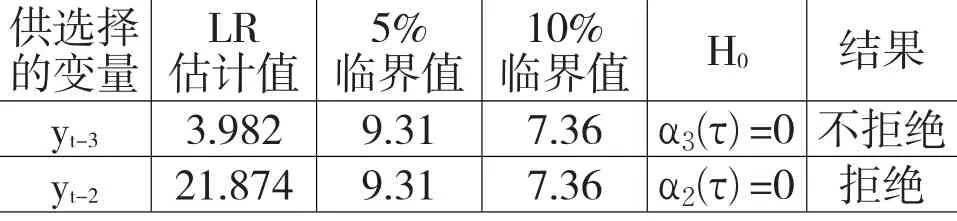
表1 模型自回归阶数的选择

最终模型是yt= α0(τ)+ α1(τ)yt-1+ α2(τ)yt-2，与此模型相关的ADF方程是yt=μ0+ α1,tyt-1+ α2,t△ yt-1+ut，其中，α2,t=-α2(Ut),ut=α0(Ut-μ0)

2.债务上限确定与局部平稳性检验

基于QAR模型，可以估计历史的债务上限以及预测未来的债务上限。比较历史债务上限与实际负债水平不仅可以检验模型合理性，还可以分析历史负债状况；估计未来的债务水平则有助于预测未来的政府负债状况并对其风险进行评估。

为了确定重庆市债务上限，本文采用Koenker和Xiao（2004）提出的t比率检验（tn(τ)）。原假设不仅包括对模型系数的假设，还包括对模型ADF函数的假设：H0∶α1,t=1。利用R软件可得到表2的结果。

表中第2栏是模型中自回归的每个十分位数估计值。上文已经假设是对τ的单调递增函数，那么α1,t也是对τ的单调递增的函数。因此，随着十分位数的不断增大，也在不断增大并接近于1。当τ∈[0.1,0.4]时，模型拒绝原假设，也就是系数不等于1，此时债务满足可持续性条件；当τ∈[0.5,0.9]时，模型无法拒绝原假设，也就是不满足债务可持续性条件。所以，模型的关键分位数τcrit=0.4，对应的重庆市债务上限为=Qyt(0.4|Ft-1)。根据前面的结论可知，如果重庆市债务借贷规模保持在Qyt(0.4|Ft-1)之上，并在未来持续下去，那么长期来看，将最终导致债务的不可持续性，并引发债务支付危机。

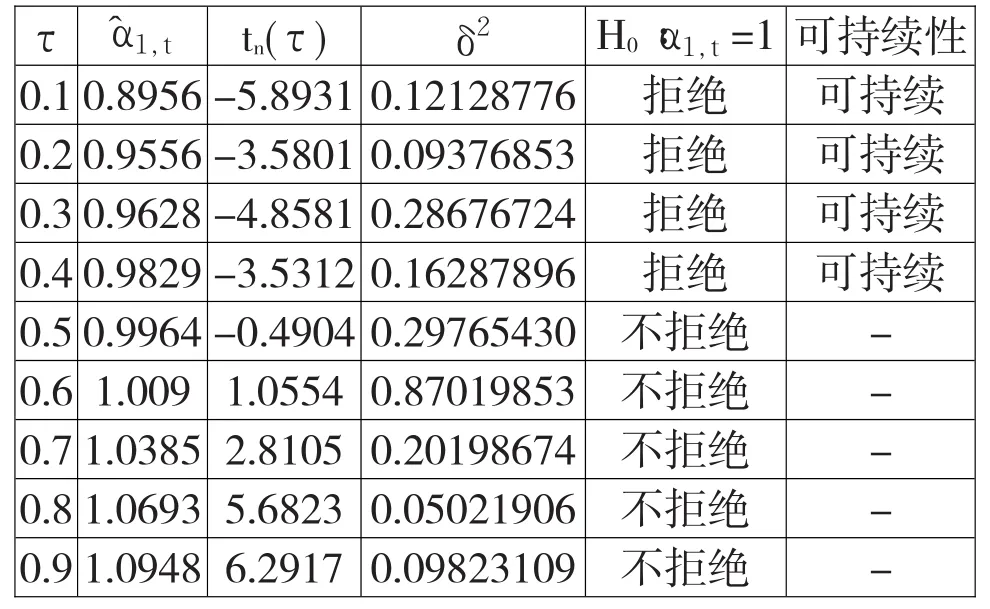
表2 Koenker—Xiao检验结果

图1中虚线表示模型估计的债务上限，实线表示实际负债率，2013E、2014E和2015E时间段则是模型预测的未来债务上限。自2008年以来，除2011年外，重庆市的实际负债水平持续高于模型估计的债务上限。此外，重庆市的实际负债率一直处于上升趋势，而债务上限在未来呈现出了较为明显的下降趋势，这反映出未来两年重庆市的债务风险将会增大。未来，重庆市政府需要合理控制新增债务规模，采取有效措施防范政府债务风险。

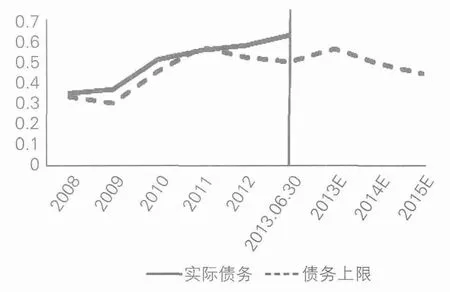
图1 重庆市政府性债务上限

（五）关键分位数的计算与分析

关键分位数τcrit为满足α1,t(τ)=＜1的条件下的最大分位数，即满足平稳性条件的最大分位数。要理解关键分位数的含义，需要先理解分位数回归。分位数回归是最小二乘回归的拓展。简单地说，最小二乘回归将样本点的均值与回归线的距离进行最小化来估计参数。如果将其中样本点的均值换成样本点的中位数或者其他分位数，就是分位数回归。选择不同的分位数，就能得到不同的回归模型参数。在QAR模型中，分位数选得越大，负债率越高。但是，并不是所有得到的参数都会使QAR模型平稳，使其平稳的最大的分位数就是关键分位数。在关键分位数下得到的QAR模型的解释变量就是债务上限，既符合“最大”负债率的含义，又能满足平稳性。可以说，关键分位数越高，得到的债务上限越高。另外，关键分位数还能够反映出负债率超出债务上限的概率。例如，某地区的关键分位数为10%，那么该地区的负债率有90%的可能性超出债务上限。关键分位数越低，实际负债率超过债务上限的概率越高，即负债状况越差。

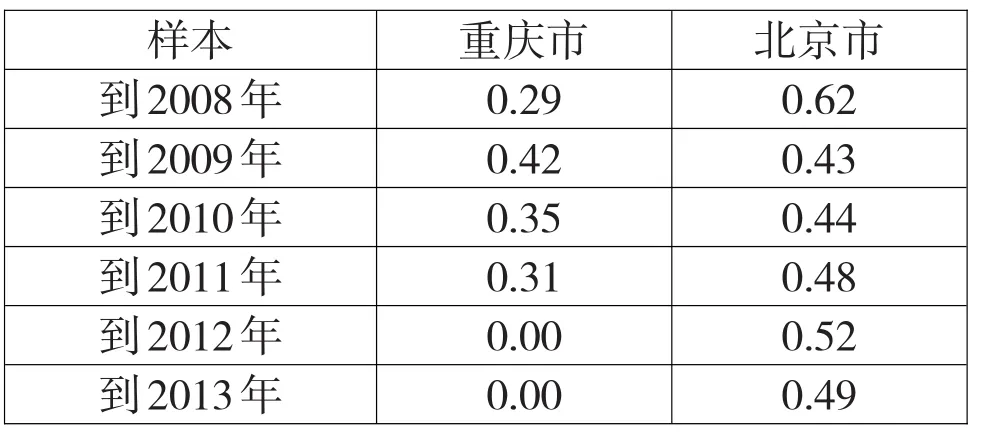
表3 重庆市的关键分位数

为了便于对比分析，本文还计算出北京市(考虑到数据的可得性)的关键分位数作为对照组，与重庆市的关键分位数进行比较。根据表3，重庆市的关键分位数明显低于北京市的关键分位数，重庆市甚至在过去两年出现了关键分位数为0的状况。这与实际经济状况是相符合的。同时，两市的关键分位数在过去六年呈现下降趋势，特别是重庆市的下降幅度较为明显，这与地区经济发展形势相符合。

四、结论与政策建议

本文通过对重庆市贴现后的负债率建立分位数自回归（QAR）模型，来求出时变负债率上限，并对未来多期的负债率上限进行预测，以及检验整体债务可持续性，对整体负债状况给出评价。QAR模型能够良好地反映某一地区的经济发展水平和负债能力。并且，模型对未来债务上限的预测也具有合理性。根据模型的结果，样本期间内重庆市政府性债务负担较重，债务承受能力较弱，债务风险较大。

针对各级地方政府性债务存在的问题，本文现从中央政府（制度层面）、地方政府（法律层面）以及城投债的参与者（市场层面）三个层面提出政策建议。首先，在中央政府（制度上）层面，中央政府应合理划分中央和地方政府税种，健全地方财政管理体制，并加强对于地方政府性债务的事前监督管理，降低地方政府对土地融资的依赖。其次，在地方政府（法律上）层面，地方政府应合理控制举债规模和举债时机，建立健全地方政府举借债务的法律体系，有效约束地方政府的借债行为。再次，在参与者（市场上）层面，评级机构应该建立地方政府性债务的评级量化模型，定期向市场公布，供投资者参考，借助市场监督约束地方政府的借债行为。

[1]周子康，金江明.国债可持续性的理论分析及检验[J].管理现代化，2003，（4）：40-44.

[2]涂立桥.我国国债可持续性的研究[J].统计与决策，2005，（4）：106-107.

[3]陈建奇.庞氏骗局、动态效率与国债可持续性[J].世界经济，2006，（12）：63-73.

[4]吴许璐，王亚芬.我国债务规模可持续性分析[J].合作经济与科技，2010，（1）：4-6.

[5]李辉文.中国公共债务与财政可持续性分析——基于结构突变BP法的实证结果[J].经济问题，2013，（11）：86-89.

[6]洪源，李礼.我国地方政府债务可持续性的一个综合分析框架[J].财经科学，2006，（4）：96-103.

[7]刘立峰.地方政府建设性债务的可持续性[J].宏观经济研究，2009，（4）：46-50.

[8]Koenker,R and Bassett,G.Regression Quantiles[J].Econometrica,1978,(46):33-50.

1003-4625（2014）11-0018-05

F812.7

2014-08-14

本文得到国家社科基金项目“发达经济体主权债务可持续性及我国对策研究”(12CGJ027)和对外经济贸易大学研究生科研创新项目“地方政府债务风险评估和安全规模测算”（A2012053）的支持。