基于双门限和证据理论的合作频谱感知算法
2014-04-03吕守涛刘健陈红宇
吕守涛, 刘健, 陈红宇
LV Shoutao1, LIU Jian2, CHEN Hongyu1
1.电子科技大学 通信与信息工程学院,四川省 成都市 611731
2.北京科技大学 计算机与通信工程学院,北京市 100083
1.School of Information and Communication Engineering, University of Electronic Science and Technology of China(UESTC),Chengdu, Sichuan 611731, China
2.School of Computer Science and Communication Engineering, University of Science and Technology Beijing(USTB), Beijing 100083, China
1 引言
当前各种无线通信业务正在快速增长,频谱资源也变得越来越紧张。采用认知无线电技术[1]则可以提高频谱资源利用率,缓解频谱资源紧张的状况。认知用户通过接入处于空闲状态的授权频段进行通信传输,减少了由于频谱空闲带来的频谱资源的浪费。认知用户使用授权频段的前提是不能对主用户造成干扰,因此频谱感知技术是认知无线电中的关键技术。
合作频谱感知技术由于能够克服单节点频谱感知中的阴影衰落、多径效应和隐藏终端等问题带来的影响而受到了广泛关注[2-4]。但是,合作频谱感知技术的频谱感知开销是非常大的,同时,在融合中心接收到各个认知用户发送过来的本地感知结果后,采用何种方式进行融合对于合作感知的性能会有很大的影响。例如,采用D-S证据理论进行融合要比采用“与”、“或”等硬判决方式融合的准确度要高很多,但是其复杂度也会相应的增加,这导致了融合中心的功率开销和计算时延也相应的增加。
Jing Li[5]提出了一种基于双门限和证据理论的可信合作感知算法。在该算法中,各认知用户采用双门限计算本地感知信任度函数,并将计算所得到的信任度函数在融合中心处利用证据理论合并规则融合,以得出最终判决。该算法由于不进行本地判决,而是在本地计算信任度函数,将所计算的信任度函数直接传送到融合中心,由融合中心进行最后的合并。该算法虽然能够提高检测性能,但是其网络开销较大,并且融合中心的计算负担过重,通常都会同时使用节点选择机制来克服上述的问题。
因此,针对上述的问题,在本文中我们提出了一种新的基于双门限和D-S证据理论的合作频谱感知算法。该算法在进行本地感知的时候,认知用户通过双门限能量检测可以直接得到判决结果的话,只需将1bit的0和1作为结果发送给融合中心。这样就大大减少了传输感知结果带来的网络开销。同时,由于双门限的使用,也使得本地判决的可靠性得到了增加。另外,只有当认知用户感知到的能量值是在两个门限之间时才会计算并发送D-S证据理论信任度函数给融合中心,这样也减少了融合中心利用D-S证据理论进行软融合的计算量,从而保证了整个合作感知算法的可靠性,并减少了融合中心的负担。
通过计算机仿真,并与常见的合作频谱感知算法进行比较可以看出,本文所提出算法的检测概率比其他检测算法的检测概率性能最大可提升30%,其接收机操作性能曲线(ROC)性能,比性能较好的D-S证据理论提升3%。
2 双门限能量检测和D-S证据理论
当前频谱感知技术按照参与感知的用户节点数目可以划分为单节点频谱感知和合作频谱感知两大类。单节点频谱感知是指每个认知用户独立完成对周围频谱状况的感知,对于频段中是否有主用户出现进行判决。常见的检测技术包括能量检测[6]、循环平稳特征检测[7]、匹配滤波器检测[8]和协方差矩阵检测[9-10]等。而合作频谱感知则是需要多个认知用户相互协作完成,认知用户之间通过信息交互,得到一个统一的感知结果。从融合算法上来划分,合作频谱感知算法包括:基于硬判决的合作感知、基于软融合的合作感知、基于分布式算法的合作频谱感知、基于分簇的合作感知和基于中继的合作感知等。
2.1 双门限能量检测
在本文算法中,认知用户获取本地感知结果时需要先进行双门限能量检测。这里先介绍一下单门限能量检测,通常使用的单门限能量检测算法,是将接收到的能量值与门限进行比较,如果能量值大于门限值,则认为主用户是存在的,否则认为主用户是不存在的。
与一般的单门限能量检测相比,双门限能量检测则是使用了两个门限来得出判决结果。通过双门限的使用,可以提高得到的判决结果的可靠性。在双门限能量检测中,当认知用户经过能量检测器获取到能量值Yi之后,与两个门限λL和λH(λL<λH)进行比较。当 Yi<λL时,认知用户可以直接做出H0判决,即认为主用户不存在,这里用1bit的“-1”表示。而当 Yi>λH时,则认为主用户是存在的,做出H1判决,用“1”表示。如果认知用户的检测统计量λL<Yi<λH,则认为认知用户是无法根据双门限检测做出本地判决的,需要延后进行判决:
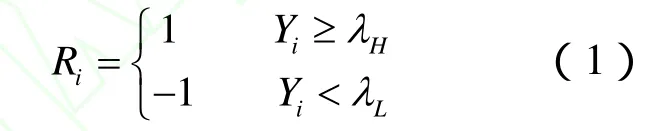
其中,Ri即为第i个认知用户得到的本地判决结果。显然,只有当Yi落在两个门限值之外时认知用户才可以直接得到Ri。而对于认知用户不能直接做出判决的能量值,本文算法则利用D-S证据理论来处理。通过双门限的使用,可以认为得到的本地判决是比较可靠的,而对于不能判决的统计量,通过使用D-S证据理论计算信任度函数,以及证据理论的合并规则来处理,可以提高得到的判决结果的可靠性。从而使得总体的检测可靠性得到保证,同时也能够减少认知用户传输感知结果带来的网络开销。
2.2 D-S证据理论
证据理论是由美国哈佛大学数学家 A.P.Dempster首先提出,由他的学生G.Shafer进一步发展起来的一种处理不确定性的理论,因此又被称为D-S证据理论。证据理论属于人工智能的范畴,可以用来处理不确定性信息。因此在医学诊断、目标识别、军事指挥等许多领域都得到了应用。在认知无线电的频谱感知当中,由于噪声等因素的影响,每个认知用户本地感知得到的检测量也是具有不确定性的,因此可以在合作感知中使用D-S证据理论来处理这些不确定信息。
在证据理论当中,采用Ω表示变量的所有可能取值的集合,且该集合中的每个元素相互独立,Ω被称为识别框架。由Ω的所有子集构成的集合称为幂集,记为2Ω。由此可以得到基本概率指派函数m的定义: m :2Ω→ [0,1],且满足:
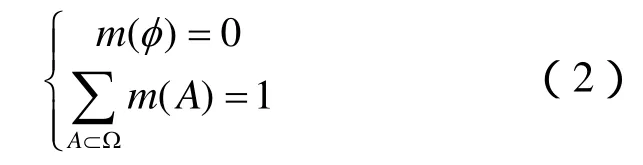
m(A)称为A的基本概率指派,m(A)表示根据当前的环境,对假设集合A的信任度,也叫做证据。在基本概率指派的基础上可以得到信任函数Bel和似然函数Pl的定义:
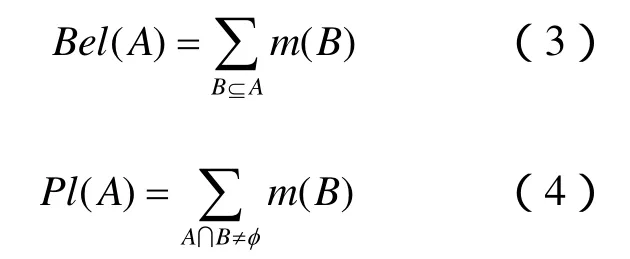
信任函数Bel(A)表示对假设集合A的总信任度,其值为A的所有子集的基本概率之和。似然函数Pl(A)表示对A为非假的信任度。
在实际问题中,由于数据来源的不同,相同的假设集合可能会得到不同的概率指派函数,而通过证据理论中的证据合并规则,可以由两个基本概率指派函数对其求正交和从而得到一个新的证据:

其中,合并的条件为B∩C≠φ,m1(B)≠0和m2(C)≠0。若B∩C=φ则称B与C矛盾。
3 算法介绍
本文算法可以分为三个步骤:
(1)认知用户进行本地双门限感知,以获取本地感知结果;
(2)当认知用户感知到的能量值在两个门限之间时,计算并发送D-S证据理论信任度函数给融合中心,融合中心对接收到的信任度函数进行融合;
(3)融合中心结合接收到的本地判决信息,进行最终判决。
算法具体过程如下:每个认知用户先进行本地的双门限感知,然后将得到的本地判决结果或者信任度函数作为感知结果发送给融合中心。融合中心首先利用证据理论的合并规则将接收到的信任度函数进行融合,得到一个由证据理论给出的判决,然后再结合接收到的本地判决信息给出一个总的判决。
3.1 本地感知结果的计算
认知用户首先要进行双门限的能量检测,下面介绍双门限的具体计算过程。
在单门限能量检测下,每个认知用户的检测概率和虚警概率如下[11]:
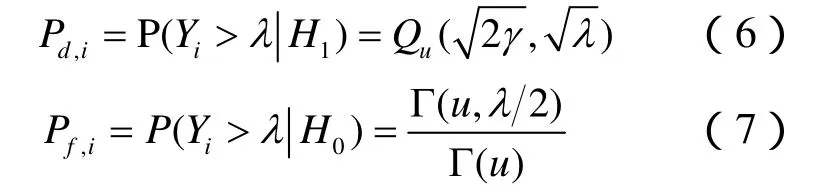
其中,u=N/2=TW,表示时间带宽积,Γ(·,·)表示非完全Gamma函数,而Q(·)为一般Marcum Q函数,γ是信噪比。
由式(6)和式(7)可以得到:

而由非完全和完全Gamma函数定义可知:


当给定Pf,i后,就可以得到单门限能量检测时的门限值λ,在此基础之上,即可以得到两个门限值:

其中,c1和c2是两个给定的常系数,且满足c1<1<c2,可以通过大量的测试选出合适的值,在本文后面的仿真时,会给出具体的值。
当计算得到了两个门限值之后,就可以根据式(1)得到认知用户的本地判决Ri。对于介于两个门限之间的Yi值,本章算法采用D-S证据理论来计算得到信任度函数。当N值比较大的时候,根据中心极限定理,检测统计量Yi的分布可以近似成为高斯分布,于是可以得到信任度函数的计算公式:
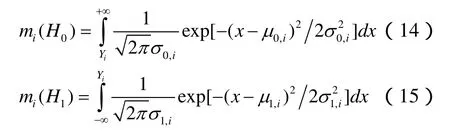
其中,µ0,i=N、=2N分别表示Yi在H0假设下的均值和方差,而µ1,i=N(1+γ),=2 N(1+2γ)分别表示Y在H假设下的均值和i1方差。
这样的话,就可以得到认知用户的本地感知结果:当Yi<λL或者Yi>λH时,得到的本地感知结果是认知用户的本地判决Ri,可以由式(1)得到;当λL<Yi<λH时,得到的本地感知结果是信任度函数mi(H0)和mi(H1),可以由式(14)和式(15)计算得到。
3.2 信任度函数的融合
融合中心接收到认知用户发送过来的信任度函数后,采用证据理论的合并规则进行融合[12],然后给出由信任度函数得到的判决结果。
具体的计算公式如下:

由式(16)和式(17)可以得到融合之后的信任度函数m(H0)和m(H1),然后可以得到判决结果:

3.3 最终判决
考虑到参与合作感知的认知用户处在不同的信道环境当中,其感知结果的可靠性也会受到环境的影响。为了使得算法总的判决结果更可靠,在这里根据信噪比来给每个认知用户的感知结果加上一个加权系数wi。每个认知用户的加权系数由如下公式得到:
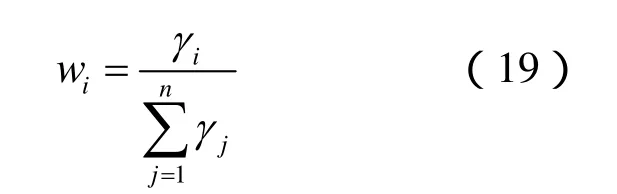
其中,n表示参与合作感知的认知用户的数量,γi表示第i个认知用户的信噪比,融合中心根据下式给出总的判决结果:

上式中,k表示经过双门限检测之后,不能够直接得到本地判决结果的认知用户数量。相应的,n-k就代表了可以直接得到本地判决的认知用户数量。
4 仿真与性能分析
具体的仿真参数设置如下:参与合作频谱感知的认知用户数n=5,认知系统中有一个主用户,同时还有一个融合中心。虚警概率设定为 0.01,c1=0.8,c2=2,这样就可以计算出具体的两个门限值,时间带宽积u=10。假定传输信道是不受阴影衰落的影响;信道增益是恒定的;并且认知用户的本地判决结果在发送给融合中心时是无差错的。五个认知用户中有四个用户的信噪比为0dB,在本章的仿真过程中,是将第五个用户的信噪比用作仿真变量以反映几种感知算法在不同信噪比条件下的感知性能。
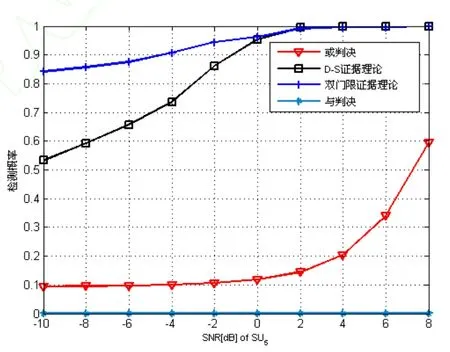
图1 几种合作感知算法的检测概率比较
从图1中可以看出在相同的信噪比环境下,本章提出的合作感知算法的检测概率明显高于其他几种检测算法,尤其是当信噪比较低的时候,采用一般D-S证据理论的合作频谱感知算法和“或”判决算法的性能都不如本章所提出的算法。当信噪比SNR=-1 0dB时,本文提出的算法的检测概率已达到 85%左右,而其他的几种检测算法,只有基于D-S证据理论的合作频谱感知算法达到了 50%以上。由此可见本章提出的算法在对于主用户信号的检测在性能上具有较大的优势,在实际应用中能够很好的保护主用户正常工作不受干扰。
如图2所示,这是几种不同合作感知算法的接收机操作特性曲线(ROC)比较图。这里设五个认知用户的感知信道信噪比分别为:-12dB、0.5dB、0.8dB、-1.2dB和1.3dB,然后设定不同虚警概率值的条件下,仿真得到了几种感知方法的检测概率图。从图中可以看出,在给定虚警概率和信噪比的条件下,提出的双门限证据理论合作感知算法性能是最优的。这说明通过信噪比计算得到加权系数来反映不同环境下认知用户的感知结果的可靠性,也使得算法的性能得到了保证。

图2 ROC比较图
5 结论和展望
频谱感知是认知无线电的关键技术,是认知用户利用空闲频段进行通信的前提和基础。通过使用双门限能量检测技术,保证了认知用户本地判决结果的可靠性。而对于介于两个门限之间的能量值,则通过计算并发送 D-S证据理论的信任度函数给融合中心,从而保证了整个合作感知算法的有效性和可靠性。并且当认知用户能够做出本地判决时只需发送本地判决结果给融合中心,减小了网络开销以及融合中心的融合计算负担。通过仿真并与常见的合作频谱感知算法进行比较可以看出,本文所提出的算法的检测概率比其他检测算法的检测概率性能提升30%,其接收机操作性能曲线(ROC)性能,比性能较好的D-S证据理论提升3%。
本文下一步的工作主要集中在以下两个方面:一是本文所提出的基于双门限和证据理论的合作频谱感知算法,是对每个认知用户都采用给定虚警概率计算得到一个统一的门限值,然后再乘上系数得到双门限值。对门限值的设定没有考虑认知用户的感知环境的差异,今后的工作则需要考虑每个认知用户的感知信道的差异性来单独计算自己的本地感知门限值,从而进一步提高感知结果的可靠性。二是本文所采用的合作频谱感知模型中,是假设参与合作感知的认知用户中是没有恶意用户存在的。如果有恶意用户存在,一直发送错误的感知信息,则会对整个合作感知的可靠性带来很大的影响,如何在融合中心处鉴别筛选出恶意用户的存在,消除恶意用户的干扰,也是下一步的一个研究方向。
[1]J.Mitola III, G.Q.Maguire.Cognitive radio:Making software radios more personal [C]IEEE Pers.Commun.,vol.6, no.4, Aug.1999, 13-18.
[2]Ian F.Akyildiz, Brandon F.Lo, Ravikumar Balakrishnan.Cooperative spectrum sensing in cognitive radio networks:A survey [J].Physical Communication, 19 Dec.2010.
[3]S.Mishra, A.Sahai, R.Brodersen.Cooperative sensing among cognitive radios[C], Proc.of IEEE ICC 2006, vol.4, 2006, pp.1658 1663.
[4]L.Y.Li, X.W.Zhou, H.B.Xu, Simplified relay selection and power allocation in cooperative cognitive radio systems [J], IEEE Trans.on Wireless Communications, vol.10, no.1, Jan.2011.
[5]Jing Li, Jian Liu, Keping Long, Reliable Cooperative Spectrum Sensing Algorithm based on Dempster-Shafer Theory, IEEE Globecom2010, Miami, FL, USA, pp:1-5,Dec.2010
[6]H.Urkowitz.Energy detection of unknown deterministic signals[C], Proc.of the IEEE, April 1967, 523-531.
[7]W.A.Gardner.Signal interception:a unifying theoretical framework for feature detectiort.IEEE Trans.on Communications [J], Aug.1988, 36(8).
[8]J.Gproakis.Digital Communications[M], 4thed.New York:McGraw·Hill, 2001, 163-233.
[9]Y.Zeng and Y.C.Liang.Covariance based signal detections for cognitive radio[C], IEEE DysPAN 2007, Apr.2007, 202-207.
[10]Y.Zeng and Y.C.Liang.Eigenvalue based sensing algorithms[EB]. IEEE document number:802.22-06/0118-00-0000,Jul. 2006[2012].http://grouper.ieee.org/groups/802/22/Meeting_document s/2006_July/22-06-0118-00-0000_I2R-sensing.doc.
[11]F.F.Digham, M.S.Alouini and M.K.Simon.On the energy detection of unknown signals over fading channels[C], ICC’03, 2003, Vol.13:3575–3579.
[12]N.T.Nhan, I.Koo, Evidence-theory-based cooperative spectrum sensing with efficient quantization method in cognitive radio [J], IEEE Trans.on Vehicular Technology,vol.60, no.1, Jan.2011.
