三次Hermite插值曲线的能量优化

2014-04-03韩旭里

计算机工程与应用 2014年12期

关键词：光顺插值导数

裴芳，高屾，韩旭里

PEI Fang1,GAO Shen1,HAN Xuli2

1.山西财经大学应用数学学院，太原 030006

2.中南大学数学科学与计算技术学院，长沙 410083

1.College of Applied Mathematics，Shanxi University of Finance&Economics,Taiyuan 030006,China

2.School of Mathematics and Computing Technology,Central-South University,Changsha 410083,China

1 引言

在计算机辅助几何设计中，构造一条满足给定端点条件的光顺曲线是一个基本问题。几何Hermite插值（Geometric Hermite Interpolation，GHI），要求插值给定端点及端点处的切方向和曲率等条件，在几何造型和工程设计中有着广泛的应用。目前国内外学者在这方面作了大量的研究，文献[1-11]分别从不同的角度研究了几何Hermite插值曲线。一般地，几何连续的条件要弱于参数连续的条件。三次几何Hermite插值曲线只具有G1连续性。本文要在保持C1连续性的前提下，实现三次Hermite插值曲线的优化问题。

2 插入两个节点的三次Hermite插值曲线

则曲线 p(u)的表达式为：

其中，hi=ui+1-ui，t=(u-ui)/(ui+1-ui)，u∈[ui，ui+1]，ui为 pi点对应的参数值[12]。

上述分段三次Hermite插值曲线 p(u)在节点处是C1连续的，而几何Hermite插值在节点处的连续性由C1降为G1，获得自由度，实现对插值曲线形状的修改。本文保持曲线在节点处C1连续，通过在每个参数区间插入两个节点，增加自由度，实现对三次Hermite插值曲线p(u)的几何优化。

在参数区间[ui，ui+1]插入两个节点和，且令：

构造C1连续的三分段次Hermite插值函数 p(u)，使之满足如下条件：

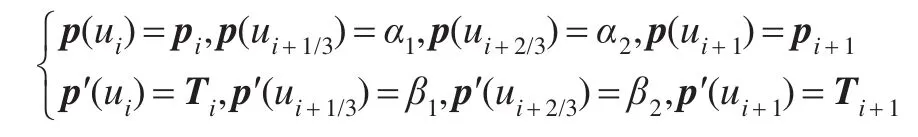
其中，α1、α2、β1和β2是四个自由变量。

通过推导，得到插值曲线 p(u)表达式如下：

3 三次Hermite插值曲线的优化

光顺性是一个在CAGD中应用很普遍又很重要的概念，国内外许多学者对此作了大量研究，提出了很多光顺方法，如Kjellander法、量法及最小二乘法等[13]。其中，能量法是一种整体优化方法，其光顺效果好，为人们普遍采用的一种曲线光顺方法。光顺法的关键是：能量函数的确定，优化问题的求解。

对于曲线 p(u)，一般选用 ∫||p(u)″||2du 和 ∫p‴(u)du 作为曲线的能量函数。其中，p″(u)为 p(u)的二阶导数，体现了曲线的曲率因素。 p‴(u)为 p(u)的三阶导数，体现了曲线的挠率因素。由于上述两个能量函数不依赖曲线的参数化，能取得较好的光顺效果，且计算量较小，便于在计算机上实现，故在曲线光顺优化中得到了普遍的应用。

3.1 基于曲率的能量函数对曲线进行优化

对于曲线式（2），在区间 [ui，ui+1]上，考虑曲线的曲率因素，定义能量函数为：

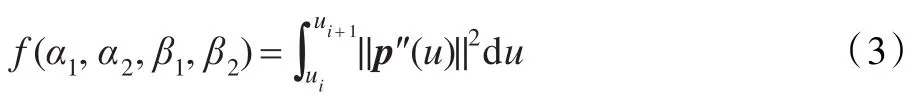
其中，u∈[ui，ui+1]，||·||表示向量的范数。

下面讨论当自由变量 α1，α2，β1，β2取何值时，曲线p(u)的能量函数 f(α1，α2，β1，β2)最小。

对曲线式（2）求二阶导数得：

这里，

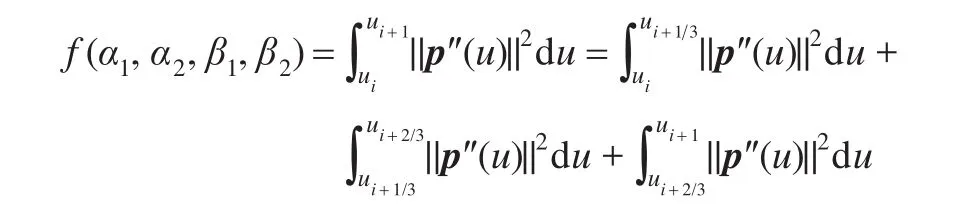
为使能量函数值最小，必须满足：

经化简得：

进而得：

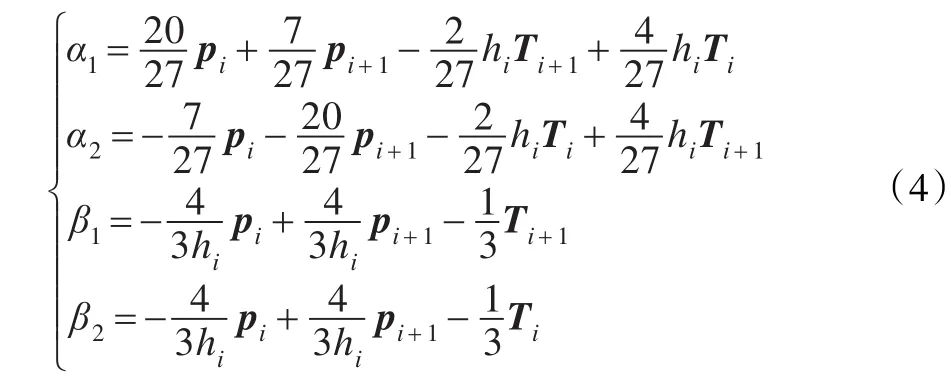
即当 α1，α2，β1，β2满足式（3）时得到的曲线 p(u)是能量函数 f(α1，α2，β1，β2)最小的曲线。

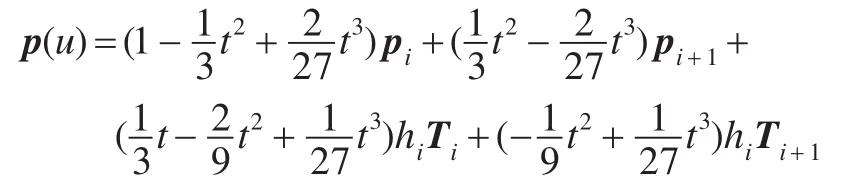
此时，对于曲线式（1），

即在区间 [ui，ui+1/3]，曲线式（1）和曲线式（2）的表达式在本质上是一致的。

同理可得，在区间 [ui，ui+2/3]、[ui+2/3，ui+1]，曲线式（1）和曲线式（2）的表达式在本质上也是一致的。

由此可得，未插入节点时所构造的分段三次Hermite插值曲线式（1）与插入两个节点时所构造的插值曲线式（2）在各区间的表达式是一致的。即以式（3）为能量函数的约束条件下，插入节点与不插入节点的情形是一致的，这体现了三次Hermite插值曲线本身所具体的特性。

3.2 基于挠率的能量函数对曲线进行优化

对于曲线式（2），在区间 [ui，ui+1]上，考虑曲线的挠率因素，定义能量函数为：

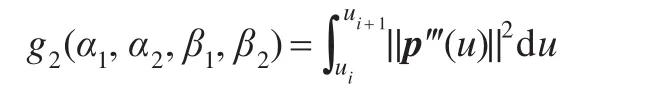
其中，u∈[ui，ui+1]，p‴(u)表示 p(u)的三阶导数。

下面讨论当自由变量 α1，α2，β1，β2取何值时，曲线p(u)的能量函数 g(α1，α2，β1，β2)最小。

对式（2）求三阶导数得：

这里，

为使能量函数值最小，必须满足：

其中β2是一个自由度，可用来调整曲线的形状。即当参数 α1，α2，β1，β2满足式（5）时得到的曲线 p(u)使能量函数 g(α1，α2，β1，β2)最小。得到了一种新的曲线构造方法，具有新的几何意义。

（1）参数a作用

下面通过对a取不同值时的插值曲线的分析来讨论参数a对曲线的调节作用。取插值区间[u0，u1]为[-1，1]，插值点及对应的切向量分别为：

取b为固定值，例如b=0.66，a取不同的值进行曲线插值。如图1所示，实线表示未优化的三次Hermite插值曲线，虚线表示a=0.8时的优化后的三次Hermite插值曲线，点虚线表示a=1.2时的优化后的三次Hermite插值曲线[14]。经过观察可以发现，参数a越小时最值点越向右移动，这表明曲线是可以水平方向上修改的。这体现了较好的实际应用价值。

图1 能量最小条件下a取不同值的三次Hermite插值曲线

表1 插值点及其切向量

（2）参数b作用

取与图1一致的插值点与对应切向量进行作图。这里取a为固定值，例如a=1.0，b取为不同的值进行曲线插值。如图2所示，实线表示未优化的三次Hermite插值曲线，虚线表示b=0.4时的优化后的能量最小的三次Hermite插值曲线，点虚线表示b=0.6时的优化后的能量最小的三次Hermite插值曲线，星号线表示b=1.0时的优化后的能量最小的三次Hermite插值曲线。经过观察可以发现，b越大时最值点越向下移动，这表明曲线是可以垂直方向上修改的。这也具有一定的应用价值。

图2 能量最小条件下b取不同值的三次Hermite插值曲线

4 图例

取表1所示的插值点及对应的切向量进行作图。随着自由参数β2取值的不同，分别得如图3所示的优化后的三次Hermite曲线。

图3 β2取不同值的优化后的三次Hermite插值曲线

5 结论

在给定插值点的位置矢量及切矢量的情况下，通过在两相邻节点引入两个新的节点，提出了一类保持C1连续的三次Hermite插值曲线的构造方法。如果以基于曲率的能量函数对曲线进行优化，证明了插入节点与不插入节点的情形是一样的，体现了三次Hermite插值曲线本身所具有的一种特性。如果以基于挠率的能量函数对曲线进行优化，给出了能量最小化的参数取值公式，含有一个自由度，可实现对曲线形状的调整。实例表明了方法的有效性。

[1]李建军.一类三次几何Hermite插值及其优化[J].数学理论与应用，2008，28（1）：155-201.

[2]吴宗敏.参数有理三次GC2Hermite插值[J].高校计算数学学报，1993，15（2）：70-76.

[3]徐良敏，孟勇.空间曲线的几何Hermite插值问题[J].计算机辅助设计与图形学学报，2001，13（2）：158-162.

[4]宋家宏，李成，王建华.空间曲线的高阶几何Hermite插值[J].计算机辅助设计与图形学学报，2004，16（6）：789-794.

[5]雍俊海，郑骏恒.一类五次PH曲线的Hermite插值的几何方法[J].计算机辅助设计与图形学学报，2005，17（5）：990-995.

[6]Hagen H.Variational design of smooth rational Bezier curves[J].CAGD，1991，8：393-399.

[7]Hosaka M.Theory of curve and surface synthesis and their smooth fitting[J].Information Processing in Japan，1969，9：60-68.

[8]Kjellander J A P.Smoothing of cubic parametric splines[J].CAD，1983，15（3）：175-179.

[9]Imre J.Cubic parametric curve of given tangent and curvature[J].Computer Aided Geometric Design，1998，30（1）：1-9.

[10]Han Xuli.Cubic trigonometric polynomial curves with a shape parameter[J].Computer Aided Geometric Design，2004，21（6）：535-548.

[11]Hollig K，Koch J.Geometric Hermite interpolation[J].Computer Aided Geometric Design，1995，13（6）：567-580.

[12]苏步青，刘鼎元.计算几何[M].上海：上海科学技术出版社，1980.