基于线性判别边信息结合PHL的三维人脸识别

关健生

GUAN Jiansheng

厦门理工学院 电气工程与自动化学院，福建 厦门 361024

School of Electrical Engineering and Automation,Xiamen University of Technology,Xiamen,Fujian 361024,China

人脸识别系统通常使用人脸图像识别特定的身份，已广泛应用于生物特征认证的人机交互中，如视频监控和访问控制等[1]。最具代表性的人脸识别方法有主成分分析（Principal Component Analysis，PCA）[2]、线性成分分析（Linear Discriminant Analysis，LDA）[3]、独立主成分分析（Independent Component Analysis，ICA）[4]等，这些方法在非限制条件下均能取得良好的效果，但是，在处理带有光照、姿态、表情及场景变化的三维人脸识别问题时，效果并不是很理想。

为了解决三维人脸识别问题，学者们提出了许多用于提高非限制条件下人脸识别性能的算法，例如，文献[5]提出了一种建立在数据源分析基础上对典型人脸识别算法进行后处理的方法，有效地提高了现有典型识别算法的识别性能在无约束环境下的鲁棒性。为了在嵌入式系统中实现实时视频图像人脸识别，文献[6]提出了基于TI系列TMS320DM642的快速人脸检测系统设计方案，测试结果表明，系统可靠运行，优化后系统运行速度提高，能够实现实时视频图像人脸识别。文献[7]提出基于B样条的多级模型自由形式形变（Free Form Deformation，FFD）弹性配准算法，先用低分辨率FFD网格全局配准，再对全局配准后的图像分块并计算对应子图块的相关性系数，对相关性系数小的子图块用高分辨率FFD网格局部细配准，在人脸畸变和表情变化很大的情况下，也能够精确配准和很好地重建，得到较高识别率。文献[8]在保局投影算法（LPP）及支持向量机（SVM）的基础上提出了一种基于相关反馈的视频人脸识别算法，通过合理的数据建模提取出视频中的时空连续性语义信息，同时能够发现人脸数据中内在的非线性结构信息而获得低维本质的流形结构，还能通过反馈学习来增加样本的标记类别。文献[9]为多姿态问题提出了基于多特征和人脸图像多特征融合的3D人脸识别方法，在这种情况下，可以使用三种方法从3D人脸图像中提取多特征：最大曲率图像、平均边缘图像、范围图像，使用权重线性组合构建融合特征。文献[10]使用最接近给定查询图像的秩作为这个查询图像的描述符。文献[11]提出了基于距离的逻辑判别和基于距离的最近邻度量方法。文献[12]提出了余弦相似性度量学习方法。最近，文献[13]提出了“关联预测”模型，利用带有较大个人内部变化的附加通用数据集来测量两幅图像之间的相似性，该模型中，每幅人脸图像与用于相似性测量的通用数据集的视觉相似对象密切相关。文献[14]提出使用属性和相似分类器输出作为人脸验证的中层特征，很好地解决了三维人脸识别问题，然而，中层特征中的跟踪比问题会在一定程度上影响识别效果。

受文献[14]启发，提出了一种原型超平面学习算法，通过使用附加的未标记的通用数据集构建SVM模型，从而得到原型超平面的中层特征表示，利用迭代优化算法求解目标函数，所得非零组合系数自动决定每个原型超平面用于三维人脸识别，利用SILD[15]进行降维，余弦相似性度量完成人脸的识别，实验结果表明了本文算法的有效性。本文的主要贡献在于：（1）将中层特征中的跟踪比问题定义为回归问题，通过最大化弱标记数据集的判别能力解决目标函数；（2）通过迭代优化算法来求解目标函数，所得到非零组合系数自动地决定每个原型超平面；（3）文献[14]中SVM模型使用附加的强标记训练集，不同于文献[14]，本文算法只从未标记通用数据集中选择支持向量稀疏集，简化了整个算法过程；（4）利用不同特征和不同特征类型进行大量实验，比较了各种情况的识别结果，表明了原型超平面学习算法的有效性。

1 跟踪比问题

（1）原型超平面的中层特征表示：本研究中，使用线性SVM对每个原型超平面建模，其中支持向量从大型未标记通用数据集χ中自动选择。注意：使用核变换可以很容易地将这里的线性SVM模型扩展成非线性，使用表现定理，特征的权重向量w可定义为：

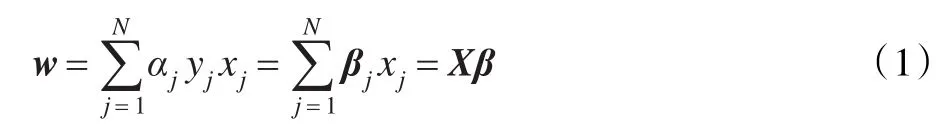
上式中，αj和 yj分别为未标记数据xj的多变量和推断类标签，合并系数βj=αjyj(j=1，2，…，N)合并每个未标记样本的多变量和推断类标签，合并系数向量定义为β=[β1，β2，…，βN]T∈RN。

本研究中，xj是一个增强的低层特征（如，Gabor或LBP特征），为了避免引入SVM模型的基础项，令它的最后一项为1。

给定弱标记数据集中的任意样本z，在SVM模型的决定值为：

它测量了样本z与SVM模型的似然值，假设有C个线性SVM模型，则为每个SVM寻找合并系数向量βi(i=1，2，…，C)，定义合并系数矩阵 B=[β1，β2，…，βC]∈RN×C，则样本z的中层特征可表示为：

（2）中层特征学习：使用弱标记数据集中每个训练样本z的新的中层特征表示 f(z)，本文提出由FLD-like准则来学习最优合并系数矩阵B，注意：本文提出的方法在提供了每个样本类标签时仍能执行。具体地，本文提出在弱标记数据集上通过最小化类内散射并最大化类间散射的方法依照目标函数来学习最优B：

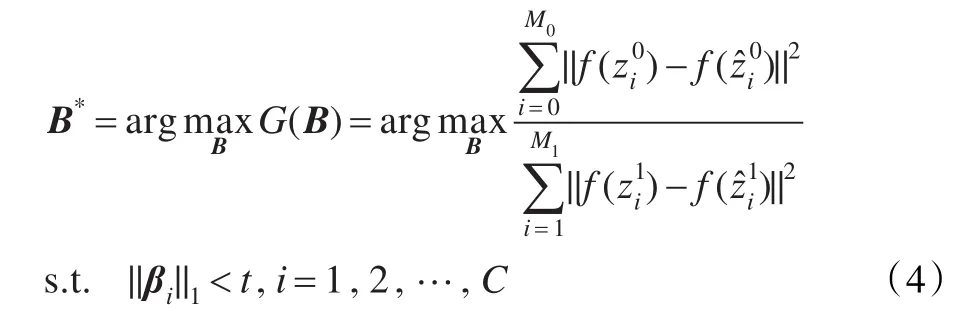
上式中，Sb和Sw定义为：

式（5）的目标函数为跟踪比形式，不存在闭合解，因此重新定义式（5）中的跟踪比问题，即

如果βi(i=1，2，…，C)没有约束条件时，求解式（7）跟踪问题的比率可以直接使用一般的特征值分解方法。然而，式（7）中的βi(i=1，2，…，C)有稀疏约束，不能使用跟踪算法求解本问题，因此，使用迭代优化算法求解最优B。

2 算法提出

2.1 原型超平面学习

首先重新定义式（7）中的目标函数，从跟踪比问题变为回归问题，这样就可以使用迭代优化方法来求解。

（1）重新定义式（7）中的跟踪比问题为回归问题：给定弱标记数据集中不同对象的M0对样本，定义两个数据矩阵：和 Hb=DTX∈RM0×N，为了定义另一个矩阵 Rw∈RN×N，先对式（6）中的 Sw进行奇异值分解（SVD），即通过引入中间变量 A=[a1，a2，…，ac]∈RN×C重定义跟踪问题为回归问题：

（2）优化式（8）的回归问题：采用一个迭代优化方法对A和B迭代优化，给定A，求解下述问题来获得B：

观察到式（9）中β1，β2，…，βC是独立的，通过优化下述问题分开求解每个βi：

使用最小角度回归求解最优βi。

给定B，忽略掉βi上的约束条件，通过求解下述问题直接计算A：

使用SVD能够获得最优A，即

上式中，U～=[u1，u2，…，uN]包含矩阵 U=[u1，u2，…，uN]前C个主导特征向量。本研究中，迭代求解式（9）和式（11），直至若干次连续迭代中B的绝对误差小于预设的阈值，详细的算法如下所示。

结果：决定SVM模型分类超平面的最优合并系数向量：β1，β2，…，βC∈RN×1

初始化：初始化 A∈RN×C和 B∈RN×C总和为1，使用式（6）计算 Sb和 Sw；通过执行 Sw的SVD，即来计算Hb=DTX∈RM0×N和 Rw∈RN×N

重复：

给定 A，求解式（10）中的独立Lasso问题得到C，使用最小角度回归：

2.2 降维和识别

有了学习原型超平面，使用式（3），每个样本都能表示成它的中层决策值特征，为了进一步降低特征维度并提高性能，采用近期提出的SLID[15]来降维，仅使用弱标记的训练数据就能学习判别性投影矩阵，当每个样本的类标签信息已知时，SILD和Fisher线性判别分析是等效的。SILD的训练过程中，仅使用相同对象的样本对定义类内散射矩阵，使用不同对象的样本对定义类间散射矩阵，使用通用的特征值分解方法决定用于降维的投影矩阵。

测试过程中，对于每对测试数据z和z^，使用学习的原型超平面分别产生对应的中层特征表示 f(z)和f(z^)，然后使用SILD训练过程学习的投影矩阵将 f(z)和 f(z^)映射到一个空间，最后，在执行人脸识别前使用余弦函数计算测试样本对的相似性。

2.3 收敛性分析

本文算法运用了迭代过程，因此，这部分对其收敛性进行了分析。

原型超平面的中层特征中，每个SVM模型的最优分类超平面由学习的合并系数βj(j=1，2，…，N)决定，特殊情况下，如果βj为0，通用数据集中未标记的样本xj会被选为SVM模型的支持向量，当支持向量是从未标记的通用数据集χ中选出时，每个支持向量的标签在学习过程之后也可以从中推断得出。如果βj是正数（或负数），yi=1（或 yi=-1）和 xj实际上可作为SVM模型的一个正样本（或负样本）来使用，而且期望SVM模型的每个分类超平面都位于两个类之间的位置，并强制β为一个稀疏向量，亦即||β||＜t，其中，t是控制β稀疏性的一个参数。式（9）中β1，β2，…，βC是独立的，式（10）通过使用最小角度回归可分别求出每个βi，利用式（9）和式（11）进行若干次连续迭代，合并系数矩阵B的绝对误差将越来越接近预设的阈值，最终目标函数必定收敛。

为了更好地表明本文算法的收敛性，在USCD/Honda人脸数据库上进行实验，参数t设置为0.5，C设置为400，实验结果如图1所示。

图1 本文算法的收敛情况

从图1可以看出，经过4次迭代后，本文算法取得了稳定的识别率，验证了其收敛性。

3 实验

实验在 USCD/Honda[5]、FRGC v2[7]、LFW[16]及自己搜集的人脸数据集上将本文算法与其他几种算法进行了比较。

3.1 基准数据集

FRGC v2数据集包含在跑步机上行走的25个人的99个视频序列，每个人有4个序列对应于4个行走模型：慢、快、倾斜和抱球（缺少了一个人的持物序列），视频中包含姿势和表情的变化，如图2所示为FRGC v2中的人脸图像示例。

图2 FRGC v2中的人脸图像示例

USCD/Honda数据集包含20个人的有姿势和表情变化的59个视频序列，平均每个对象有3.0个视频，每个视频剪辑长度在24 frame/s下约为181帧，如图3所示为USCD/Honda中的人脸图像示例。

图3 USCD/Honda中的人脸图像示例

实验在FRGC v2和USCD/Honda数据集上均使用图像限制型训练模型，即只知道某样本对是否属于同一对象或不同对象，而不知道每个样本的类标签，为了构建未标记通用数据集χ，将每幅人脸图像中心区域通过移除背景的方式裁剪为80×150像素大小。从FRGC v2数据集上随机选择300个未标记样本用作通用数据集，从USCD/Honda人脸数据集上选择图像作为训练数据集，值得注意的是，未标记通用数据集和测试集之间没有重复图像。实验的每一轮精度定义为正确分类的样本对数目除以测试样本对总数目，标准差定义为其中，是标准偏差。

3.2 参数分析

以USCD/Honda人脸数据集为例，考察了不同的原型超平面数目C和稀疏参数t对本文算法的性能的影响，包括识别的精度和整个算法所耗时间，C分别取100、200、400、600，t分别取0.1、0.2、…、0.8。实验使用MATLAB7.0在PC机上实现，计算机配置为：Windows XP操作系统、迅驰酷睿2处理器、2.5 GHz主频、4 GB RAM，如图4所示为参数C和t对本文算法识别精度的影响，图5所示为C和t对本文算法训练所耗时间的影响。

图4 参数C和t对本文算法识别精度的影响

图5 参数C和t对本文算法训练所耗时间的影响

从图4可以看出，当C设置为一个较大数时，本文算法的平均精度会更好，但同时训练时间也会增加（如图5所示）。本文也使用其他特征在USCD/Honda数据集上作了与FRGC v2数据集上类似的观察，为了权衡有效性和效率，当使用所有类型特征时，在两个数据集上都设置C=400。当设置参数t在0.2到0.8之间时，本研究的结果变得相对稳定，考虑到没有用于模型选择的预定义附加数据集，因此，后面在USCD/Honda人脸数据集上的实验设置参数t为0.5。

3.3 实验结果比较

3.3.1 FRGC v2数据集

在FRGC v2数据集上，使用八种类型的特征，包括强度特征、LBP特征、Gabor特征和分块Gabor特征及各个特征的方根，将本文算法与“低层特征+SILD”的性能进行了比较。

对于强度特征，直接通过矢量化每个灰度图像到12 000维特征向量来提取。LBP特征中，首先从每个10×10不重叠像素块提取一个59针的直方图，然后所有直方图串联成一个单一7 080维特征向量。使用40个Gabor核函数从5个等级8个方向来提取Gabor特征，为了降低特征维度，进一步使用10×10变换因子下采样Gabor滤波图像，然而，这个重要的下采样过程可能会降低人脸识别的性能。分块Gabor特征中，下采样之前将每个Gabor滤波图像划分成6个不重叠的块，每个块的Gabor滤波子图像仅使用2×2的变换因子进行下采样，然后分别对每个块的Gabor特征，而不是将它们串联成一个很长的特征向量，对于每一对人脸图像，对6个块的Gabor特征使用余弦函数计算出6个相似度，然后输出一个平均分数。为了混合8类特征，每对图像表示成一个8维相似度特征，然后采用线性SVM进一步计算每对图像最终的相似度。实验中，本文算法使用中层特征，“低层特征+SILD”使用原始低层特征，除了强度特征的方根以外，结果如表1所示。

从表1可以看出，在最终验证之前，本文算法采用SILD执行降维，在其他所有类型的特征方面执行效果均优于“低层特征+SILD”[15]，当使用Gabor特征方根时，性能提升2.55%，使用LBP方根得到的结果为86.42%，结合使用所有特征时识别率可高达89.67%。

表1 FRGC v2数据集上使用不同类型底层特征的性能（平均精度±标准差）

此外，实验直接使用文献[17]提供的三类特征（LBP、CSLBP和FPLBP），考虑到所有人脸图像都经固定的检测脸部关键点对齐过，将从一个视频剪辑所有帧中提取出的平均特征，为本文算法和低层特征+SILD的后续过程输出平均特征向量，识别结果如表2所示。

表2 各算法使用三种特征在FRGC v2上的识别结果

从表2可以看出，本文算法使用三类特征的性能明显优于“低层特征+SILD”，平均精度比“低层特征+SILD”高出3%，表明使用PHL学习分类超平面来提取特征的有效性。使用LBP特征，本文算法在ACC、AUC和EER方面性能提升比MBGS分别高出4.2%、4.9%和4.6%，使用CSLBP和FPLBP特征，本文算法也优于MBGS。

3.3.2 USCD/Honda数据集

在USCD/Honda数据集上，实验也使用文献[17]提供的三类特征，并将本文算法与“MBGS”[17]算法和低层特征+SILD算法进行比较，表3中列出了这三种算法在平均精度、曲线下方面积（AUC）和等差率（EER）方面的数据。

从表3可以看出，与表2的结果一致，本文算法使用三类特征的性能优于“低层特征+SILD”，平均精度比“低层特征+SILD”高出3%，再一次表明使用PHL学习分类超平面来提取特征是有益的。使用三种特征时，本文算法均优于MBGS。

3.3.3 自己采集的人脸数据库上的实验

由于USCD/Honda、FRGC v2视频人脸数据库的样本类型不足，通过自采集构建数据库（如图6和图7所示），数据库一共有15人，每人有16段视频，采集数据时有意安排有正脸和侧脸姿势，并有意设置不同的光照环境，同时注意面部表情的刻意变化，主要的目的是在尽可能短的时间内模拟真实视频的各种环境。实际应用中，视频时间较长，一般都会有侧脸、光照、表情的变化，因此，有针对性采集的视频数据库对基于视频的人脸识别算法进行比较实验非常合理。

表3 各算法使用三种特征在USCD/Honda上的识别结果

图6 正脸样本

图7 正侧脸样本

实验将本文算法与其他几种算法进行了比较，包括隐马尔可夫后处理模型[5]、基于合并的b/g样本的方法[10]、属性和相似分类器[1]、多级FFD配准[7]、底层特征+SILD[14]、CSML+SVM[12]、尺度不变特征融合[9]和关联预测[13]，每个人的正脸样本用于训练，正侧脸样本用于测试，比较结果如表4所示。

表4 本文算法与其他算法的识别性能比较

从表4可以看出，本文算法仅比文献[13]中的“关联预测”算法稍差，但是，“关联预测”要求有个人内部变化的强标记附加数据集，而本文提出的本文算法仅需要附加的未标记数据集，因此，相比另外几种比较算法，本文算法取得了更好的识别效果。从标准差来看，本文算法的标准差最小，表明了其稳定性优于其他各个方法。

3.3.4 户外人脸数据库上的实验

最后，在实际条件下采集的户外人脸数据库LFW上测试本文算法。实验选择包含55个对象的一个图像集，如图8所示为户外人脸图像示例。从每幅图像的背景中裁剪出人脸区域，调整大小为64×64，不同于先前在室内条件下采集到的测试图像，这些图像是在完全不受约束的现实环境中采集到的，实验将本文算法与其他几种算法进行了比较，对于每个对象，分别选择K=1，3，5，8幅未遮挡的图像作为训练集，有不同遮挡类型的110幅图像用于测试，每个训练集与探针集均不相交，比较结果如表5所示。

图8 LFW人脸数据库中的图像示例

表5 各算法在LFW上的识别性能比较

从表5可以看出，与表4的结果一致，本文算法仅比“关联预测”算法稍差，相比另外几种算法，本文算法取得了更好的识别效果。从标准差来看，本文算法的标准差最小，再次验证了本文算法的优越性。

4 结论

本文提出一种原型超平面学习算法，通过学习SVM模型的一组原型超平面寻找用于三维人脸识别的中层特征，在只从通用数据集选择稀疏样本集作为支持向量的稀疏约束条件下，通过最大化弱标记数据集的判别能力解决目标函数，学习到的SVM模型的决策值用作中层特征，使用SILD进一步降低特征维度，最后，使用余弦相似度完成最终的人脸识别。大量实验表明本文提出的方法优于其他现有算法。

未来会将本文提出的算法运用到其他的非约束人脸数据集上，并结合其他的新颖技术，进行大量实验，进一步改善三维人脸识别的性能。

[1]杨传振，朱玉全，陈耿.一种基于粗糙集属性约简的多分类器集成方法[J].计算机应用研究，2012，29（5）：1648-1650.

[2]Abdi H，Williams L J.Principal component analysis[J].Wiley Interdisciplinary Reviews：Computational Statistics，2010，2（4）：433-459.

[3]曹洁，吴迪，李伟.基于鉴别能力分析和LDA-LPP算法的人脸识别[J].吉林大学学报：工学版，2012，42（6）：1527-1531.

[4]柴智，刘正光.应用复小波和独立成分分析的人脸识别[J].计算机应用，2010，30（7）：1863-1866.

[5]代毅，肖国强，宋刚.隐马尔可夫后处理模型在视频人脸识别中的应用[J].计算机应用，2010，30（4）：960-963.

[6]邹垚，张超.基于DSP的人脸识别算法实现与优化[J].计算机应用，2010，30（3）：854-856.

[7]Kong Y，Zhang S，Cheng P.Super-resolution reconstruction face recognition based on multi-level FFD registration[J].Optik-International Journal for Light and Electron Optics，2013，124（24）：6926-6931.

[8]鲁珂，丁正明，赵继东，等.一种基于相关反馈的视频人脸算法[J].西安电子科技大学学报：自然科学版，2012，39（3）：154-160.

[9]Wijaya I G P S，Uchimura K，Koutaki G.Multi-pose face recognition using fusion of scale invariant features[C]//Proceedings of the 2011 2nd International Congress on Computer Applications and Computational Science.Berlin Heidelberg：Springer，2012：207-213.

[10]黄荣兵，郎方年，施展.基于Log-Gabor小波和二维半监督判别分析的人脸图像检索[J].计算机应用研究，2012，29（1）：393-396.

[11]Guillaumin M，Verbeek J，Schmid C.Is that you?Metric learning approaches for face identification[C]//2009 IEEE 12th International Conference on Computer Vision，2009：498-505.

[12]高全学，谢德燕，徐辉，等.融合局部结构和差异信息的监督特征提取算法[J].自动化学报，2010，36（8）：1107-1114.

[13]Yin Q，Tang X，Sun J.An associate-predict model for face recognition[C]//IEEE Conference on Computer Vision and Pattern Recognition（CVPR），2011：497-504.

[14]Kumar N，Berg A，Belhumeur P N，et al.Describable visual attributes for face verification and image search[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2011，33（10）：1962-1977.

[15]Kan M，Shan S，Xu D，et al.Side-information based linear discriminant analysis for face recognition[C]//BMVC，2011：1-12.

[16]Miranda D.The face we make[EB/OL].[2013-10-11].http：//www.thefacewemake.org.

[17]Wolf L，Hassner T，Maoz I.Face recognition in unconstrained videos with matched background similarity[C]//2011 IEEE Conference on Computer Vision and Pattern Recognition（CVPR），2011：529-534.