贝叶斯倾向评分方法及其与传统倾向评分方法的比较*

第二军医大学卫生统计学教研室(200433)

张 筱 叶小飞 张新佶 郭晓晶 吴美京 张天一 李 慧 贺 佳△

近年来，由于随机对照试验(randomized controlled trials,RCT)通常存在所选人群有限、样本量较少、随访时间较短、价格昂贵等局限性，它的大规模应用受到一定的限制。而观察性研究(observational study,OBS)通常不对研究人群进行严格的限制、样本量较大、观察时间较长、研究成本较低、可以收集到足够的信息观察到特殊人群(如孕妇、儿童、有合并其他疾病的患者)的暴露情况，也可以对罕见事件的发生做出评价[1]，因而近年来国内外越来越多的研究者采用观察性研究方法在医学领域进行大规模人群研究。但观察性研究不能像RCT那样采用随机化设计对研究对象随机分配，可能出现混杂因素在组间分布不均衡现象，产生混杂偏倚。传统的控制混杂因素的方法如分层法(当分层数目较多时会产生过度分层的问题)及logistic回归法(受模型线性假设条件的限制)存在一定的局限性[2]，因此，迫切需要更加有效的方法来均衡不同特征数据之间的差异，更为准确地控制混杂因素的影响，使不同特征的数据间具有可比性，从而更好地挖掘出数据中隐藏的信息，获得更准确的信号检测结果。目前，倾向评分法及贝叶斯倾向评分法是解决这一问题的较有力工具。

1.倾向评分法

倾向评分法(propensity score analysis,PSA)作为均衡组间混杂因素的新方法由Rosenbaum和Rubin在1983年首次提出[3]，其基本原理是将多个协变量的影响用一个倾向评分值来表示(相当于降低了协变量的维度)，然后根据倾向评分值进行不同对比组间的分层、匹配或加权，即均衡对比组间协变量的分布，最后在协变量分布均衡的层内或者匹配组中估计处理效应。在大样本的情况下，经过倾向评分值调整的组间个体，除了处理因素和结局变量分布不同外，其他协变量应该均衡可比，相当于进行了“事后随机化”，使观察性数据达到“接近随机分配数据”的效果[4-5]。

估计倾向性评分值是倾向评分法的第一步，也是核心步骤。其估计的准确与否，直接关系到组间均衡的效果，进而影响到对处理效应的正确推断。目前，常用的估计倾向评分值的模型有logistic回归、probit回归、判别分析以及数据挖掘中的神经网络、支持向量机、分类与回归树、Boosting算法等机器学习方法[6]。判别分析要求协变量服从多元正态分布，而流行病学资料中存在着较多的分类变量，因此该方法在流行病学中较少使用[7]；probit回归函数表示累积标准正态分布函数的逆函数或反函数，其结果不易解释，限制了该方法的广泛使用；数据挖掘的方法因其稳定性差、难以理解、结构复杂等缺陷，较少有研究将其应用于实际数据中[8]。

传统的倾向评分法即借助logistic回归模型估计倾向评分值，其应用最为广泛[9]。采用传统的logistic回归模型估计倾向评分值具有模型简单、容易实现、稳健性好、结果易于解释等优势。然而，其在应用中存在的问题也不容忽视：(1)通过logistic回归模型估计的倾向评分分值与其真实值的偏倚较大，而研究者未考虑到倾向评分值的不准确性对混杂因素组间均衡性的影响，进而影响到处理效应估计的准确性，特别是在倾向评分调整法和匹配法中，这个问题更为突出[10]；(2)传统的logistic回归模型估计倾向评分值时，连续型协变量与logit(y)需要满足线性关系的限制条件，当此条件不被满足时，结果的准确性将受到影响，而在实际应用中，研究者往往忽略了对此假设条件进行检验[11]；(3) 当事件发生数与协变量数之比小于10时，传统的logistic回归估计得到的倾向评分值也存在较大的偏倚[12]；(4)估计处理效应时无法利用先验信息。如果可以利用已有的信息，可有效提高处理效应估计值的精确性和可靠性；(5) 无法很好地处理缺失数据、高维数据等问题。

因此，国外越来越多的研究者开始将贝叶斯统计的思想引入到倾向评分法中，构建贝叶斯倾向评分模型，估计倾向评分值及处理效应，以弥补传统的倾向评分法无法解决的问题。

2.贝叶斯倾向评分法(Bayesian propensity score analysis，BPSA)

贝叶斯统计是将关于未知参数的先验信息与样本信息综合，并不断通过样本数据更新先前认知的统计方法。它采用马尔可夫链蒙特卡罗算法(MCMC)对估计参数的后验分布进行抽样，并结合所构建的似然函数对所估计的先前认知(即MCMC法上一次迭代的先验信息与样本信息的综合)不断地进行修正，最终得到估计参数的一个稳定的后验分布，根据后验信息去推断总体参数。贝叶斯统计是基于总体信息、样本信息及先验信息进行的统计推断。1985年，Rubin等人论证了倾向评分法与贝叶斯思想结合的合理性，首次在专著中提出将贝叶斯统计的思想引入到倾向性评分法中，但并未构建相应的模型[13]。目前，国外学者普遍认为倾向评分模型中的参数是未知的，具有不确定性及随机性，因此可以构建贝叶斯倾向评分模型，且贝叶斯倾向评分模型可以与贝叶斯因果推断模型或传统的概率统计因果推断模型相结合。围绕此种观点，现已提出了多种贝叶斯倾向评分的模型。

Hoshino在2008年提出一种半参数贝叶斯倾向评分模型，并与复杂模型相结合(如结构方程模型)，用于处理潜在变量的影响或解决多组间比较的问题[14]，但因其复杂的数理推理过程限制了模型的广泛应用。2009年，McCandless、Gustafson、Austin等人构建了另一种贝叶斯倾向评分模型[10]，可以同时估计倾向分值和处理效应。目前，此模型的应用较多。如公式(1)、公式(2)所示，其中公式(1)为结局变量的估计，X代表处理因素，β为处理因素的回归系数(即处理效应的估计)，Z(C,γ)代表公式(1)中所估计的倾向分值。公式(2)为倾向分值的估计，C代表混杂因素。

logit[Pr(Y=1/X,C)]=βX+ζTg(z(C,γ))

(1)

logit[Pr(Y=1/X,C)]=γTC

(2)

(3)

(4)

(5)

McCandless先应用贝叶斯logistic回归模型纳入候选协变量，利用先验信息，根据贝叶斯统计的思想，得出每个个体的倾向性评分值，将PS值分为五段，作为潜变量引入贝叶斯回归模型，并构建混杂因素条件下结局变量与处理因素联合分布的似然函数。他提出的BPSE算法有以下三个特点：(1)采用无信息先验分布，假定先验信息β、γ、ξ方差很大且服从正态分布，见公式(3)、(4)、(5)；(2)对倾向分值进行分层(分层节点的选择可直接选用五分位值或采用立方样条法拟合节点)，然后将倾向分值作为潜变量纳入处理效应估计的模型中；(3)借助MCMC法，利用所构建联合分布的似然函数，同时估计出处理效应的回归系数(β)、协变量的回归系数(γ)以及倾向分值的回归系数(ξ)。

如上文所述，McCandless等人构建的贝叶斯倾向评分模型将倾向分值进行分层后再作为协变量纳入结局变量的似然函数，并同时估计出倾向分值及处理效应。在其结果解释时，他将倾向分值的回归系数(ξ)当作冗余参数。而事实上倾向分值的回归系数(ξ)可以反映结局变量的估计对倾向评分估计的影响，而上述研究中忽略了此种影响关系。因此，2010年，McCandless等人又探讨了两步进行的贝叶斯回归调整法，以控制结局变量的估计对倾向分值估计的影响，更加精确地估计倾向评分值[15]。并将其应用于时依性结局变量的数据分析中(如生存分析资料)混杂因素的控制。如公式(6)表示为同时估计模型的概率密度函数，公式(7)表示分两步进行时倾向分值的概率密度函数。

(6)

(7)

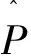
(8)

2012年，David Kaplan、Jianshen Chen等学者认为先前McCandless、An等学者所构建的贝叶斯联合分布忽略了结局变量对倾向评分分布的影响，进一步假设联合分布中若不存在结局变量，那么会产生不同的倾向分值的分布，于是提出了分两步完成的贝叶斯倾向评分法[17]。简单地说，在David Kaplan的研究中，两步的BPSA就是两个独立的过程，即估计倾向评分值时采用贝叶斯logistic模型(与McCandless、An的估计倾向分值的似然函数相同)，而用最小二乘法(如公式(9)所示，X代表处理因素，β为处理因素的回归系数即所要估计的处理效应)或贝叶斯回归估计处理效应。David Kaplan还将他提出的两步BPSA法与McCandless等人的一步BPSA法进行了比较，研究发现两步完成的贝叶斯倾向评分分层法所估计的处理效应的方差小于一步完成的贝叶斯倾向评分的分层法，但最优匹配法的结果较接近。此外，贝叶斯倾向评分法与传统的方法相比较，发现贝叶斯倾向评分法估计的处理效应的方差较大，与McCandless等人的研究结果一致。他认为传统的倾向评分法估计的处理效应的方差较小，而BPSA提供的处理效应的方差虽然略有增大然而更加准确。

Y=a+βX+ε

(9)

贝叶斯倾向评分法与传统的logistic倾向评分法对处理效应的估计哪个更加精确呢？这个问题目前尚未有统一的结论。不同方法特点不同：(1) 处理效应的估计受不同倾向评分值的利用方式的影响。如直接选用五分位值将倾向分值分为五层[10]或采用立方样条法拟合节点分为四层[18]，选用最邻近匹配法(nearest neighborhood matching)[16]或最优匹配法(optimal full matching)[17]，对结果都有影响。(2)不同贝叶斯倾向评分法选择的估计结局变量的似然函数不同[10,16,18]。如McCandless 的研究中处理效应的似然函数采用贝叶斯logistic回归，而An的研究中处理效应的似然函数采用一般线性模型。(3)先验信息分布的选择(如有研究选择有信息先验分布，也有研究选择无信息)以及超参数的设定不同。David Kaplan等人通过模拟研究证明先验信息设定的越准确，处理效应的估计越接近真值。因此，需要基于自己研究的数据特征，对不同学者提出的贝叶斯倾向评分法进行横向比较研究，筛选最优的贝叶斯倾向评分法。

3.贝叶斯倾向评分模型的实际应用

4.贝叶斯倾向评分法与logistic倾向评分法的比较

现从以下九个方面对传统的倾向评分法及贝叶斯倾向评分法进行简要的比较(如表1所示)：(1)PS值估计的准确性 可通过协变量的回归系数(γ)来反映，贝叶斯倾向评分法可以更加精确地估计γ的可信区间[10,15-16,18]。(2)模型假设 传统的logistic回归模型需要满足对数线性假设的条件，结果才更可靠，而贝叶斯倾向评分模型对此假设条件并不敏感[10]。(3)均衡性 根据国外多项研究结果，与结局相关的变量均为重要的混杂因素，需要对其进行组间均衡性检验。而与处理因素强相关、与结局变量弱相关的混杂，对结果的影响不大，可以忽略。传统的logistic回归模型主要均衡与处理因素相关的混杂，可能会遗漏掉某些与结局相关的重要的混杂；而贝叶斯倾向评分主要均衡与结局变量相关的混杂[18]。(4)缺失数据 若某个或某几个协变量存在缺失，logistic回归等传统统计方法便无法得到倾向评分值。而贝叶斯倾向评分法允许缺失数据的存在。(5)高维数据 对于高维数据，变量之间可能存在各种各样的线性及非线性关系或交互作用，贝叶斯倾向评分法在处理这些问题方面有着明显的优势。(6)潜变量(latent variable) 也称为不可测量的变量(unmeasured variable)。贝叶斯倾向评分法可以与复杂模型相结合(如结构方程模型等)，处理潜在变量的问题[14,20]。(7)样本大小或事件发生数目 当样本数较小或事件发生数较小时，使用logistic倾向评分法，结果不够稳定，而贝叶斯倾向评分法在此种情况下有着明显的优势[16-17]。(8)软件应用 传统logistic回归模型可在SAS、R、Stata等多种软件中实现，贝叶斯倾向评分则只能通过R软件计算。(9)难易程度 logistic回归模型具有简单、容易实现等特点。贝叶斯倾向评分法的实现比较复杂，需要预先确定先验分布(无信息先验分布、有信息先验分布)、设定参数的初始值、选取恰当的抽样方式(Metropolis或Gibbs抽样)，还需要借助MCMC法才能得以实现。

表1 贝叶斯倾向评分法及传统的倾向评分法的比较

5.展望

随着信息化技术的推进，在日常业务中可以通过信息系统收集大量的观察性数据，如不良反应自发呈报系统(spontaneous reporting system,SRS)[21]、医院信息系统(HIS)、电子病历(EMR)等。如何将这些数据有效利用，提供有价值的关于干预因素与结局之间因果关系的“证据”或“线索”，为医学与政策问题的研究及解决提供巨大的数据支持及循证支持，已成为统计方法学研究中面临的巨大挑战。贝叶斯倾向评分法是近年来新提出的一种处理观察性研究中混杂偏倚的有力工具，它可以有效地利用先前研究或系统累积数据中的大量信息、充分考虑倾向分值的随机性而更加精确地估计倾向评分值、与复杂模型相结合处理复杂结构的数据以及借助MCMC法快速的估计出各项参数的后验分布等，因而较传统的倾向评分法具有广泛的应用前景。目前，贝叶斯倾向评分法在应用过程中还存在着较多的问题：不同学者提出的联合分布及似然函数也不尽相同；不同研究中先验信息的设定方式不同；倾向分值的利用方式也不尽相同。以上因素都会影响到处理效应的估计结果。因此，在对观察性数据进行研究时，需要充分考虑数据特征及研究目的，选择最佳的模型进行分析。此外，目前的贝叶斯倾向评分法仅限于两分类的处理因素及结局变量，对于多分类的处理因素、随时间变化的处理因素、连续型结局变量等观察性数据中常见的问题，还需要进一步的研究。

参 考 文 献

1.Perkins SM,Tu W,Underhill MG,et al.The use of propensity scores in pharmacoepidemiologic research.Pharmacoepidemiol Drug Saf,2000,9(2):93-101.

2.王超,吴骋,许金芳,等.倾向性评分匹配法在不良反应信号检测中的应用.中国卫生统计,2012,29(6):855-858.

3.Rosenbaum PR,Rubin DB.The central role of the propensity score in observational studies for causal effects.Biometrika,1983,70:41-55.

4.张亮,李婵娟,夏结来,等.倾向得分区间匹配法用于非随机对照试验的探索与研究.中国卫生统计,2012,29(1):53-57.

5.李智文,李宏田,张乐.用SPSS宏程序实现观察对象的倾向评分配比.中国卫生统计,2011,28(1):89-92.

6.Westreich D,Lessler J,Funk MJ.Propensity score estimation:neural networks,support vector machines,decision trees (CART),and meta-classifiers as alternatives to logistic regression.J Clin Epidemiol,2010,63(8):826-33.

7.D′Agostino RB Jr.Propensity score methods for bias reduction in the comparison of a treatment to a non-randomized control group.Stat Med,1998,17(19):2265-81.

8.Setoguchi S,Schneeweiss S,Brookhart MA,et al.Evaluating uses of data mining techniques in propensity score estimation:a simulation study.Pharmacoepidemiol Drug Saf,2008,17(6):546-55.

9.Felix J.A Systematic Review of Propensity Score Methods in the Social Sciences.Multivariate Behavioral Research,2011,46:1,90-118.

10.McCandless LC,Gustafson P,Austin PC.Bayesian propensity score analysis for observational data.Stat Med,2009,28(1):94-112.

11.Bagley SC,White H,Golomb BA.Logistic regression in the medical literature:standards for use and reporting,with particular attention to one medical domain.J Clin Epidemiol,2001,54(10):979-85.

12.Cepeda MS,Boston R,Farrar JT,et al.Comparison of logistic regression versus propensity score when the number of events is low and there are multiple confounders.Am J Epidemiol,2003,158(3):280-7.

13.Rubin DB.The use of propensity scores in applied Bayesian inference.In Bayesian Statistics 2,Bernardo JM,De Groot MH,Lindley DV,Smith AFM (eds).Valencia University Press,North-Holland:Amsterdam,1985,63-72.

14.Hoshino T.A Bayesian propensity score adjustment for latent variable modeling and MCMC algorithm.Computational Statistics & Data Analysis,2008,52,1413-1429.

15.McCandless LC,Douglas IJ,Evans SJ,et al.Cutting feedback in Bayesian regression adjustment for the propensity score.Int J Biostat,2012,6(2):Article.

16.An W.Bayesian propensity score estimators:incorporating uncertainties in propensity scores into causal inference.Sociological Methodology,2010,40,151-189.

17.David K,Jianshen C.A two-step Bayesian approach for propensity score analysis:simulations and case study.Psychometrika,2012,77(3):581-609.

18.McCandless LC,Gustafson P,Austin PC,et al.Covariate balance in a Bayesian propensity score analysis of beta blocker therapy in heart failure patients.Epidemiol Perspect Innov,2009,6(5).

19.McCandless LC,Gustafson P,Austin PC.Code for fitting Bayesian propensity analysis to a toy synthetic dataset [CP/OL].http://www.biomedcentral.com/content/supplementary/1742-5573-6-5-S1.R.

20.McCandless LC,Richardsonand S,Nicky GB.Propensity Score Adjustment for Unmeasured Confounding in Observational Studies.ESRC National Center for Research Methods NCRM Working Paper Series,2,2008.

21.钱维,王超,吴骋,等.运用随机森林分析药品不良反应发生的影响因素.中国卫生统计,2013,30(2):209-213.