改进转角法的实现及在海洋测绘中的应用

2014-04-03魏荣灏李京兵史永忠

浙江水利科技 2014年3期

魏荣灏，李京兵，史永忠

（浙江省河海测绘院，浙江杭州 310008）

1 问题的提出

在海洋测绘工作中，采用验潮方法对大范围海域进行小比例尺测绘时，使用单潮位站进行水位改正的方法难以满足技术规范［1］的要求，必须进行分带潮位内插；采用多波束测深系统进行大比例尺测量时，为了保证测区数据全覆盖，获取数据常常会超出测量范围；另外，大部分多波束后处理软件常以矩形为单元处理数据，处理结果导出后往往与实际复杂的测区形状不同，测区外部经常存在多余数据，因此，必须对测区内外的数据进行筛选。采用人工方式操作时，不但费事费力，还容易出现错漏，需要反复操作，比较枯燥。若采用计算机自动处理，主要工作在于判别测点数据与测区的相对关系，即判断点与多边形的相对关系。

判断点在多边形内或外是一个基本却又非常重要的问题，在计算几何、计算机图形学、模式识别和地理信息系统中有大量的应用。为解决该问题，国内外众多学者已经进行了大量的研究，提出的算法主要可以分为2类：奇偶法（射线法）［2－4］和非零环绕数法（转角法）［2，5，6］。如果多边形是简单的（没有自相交点），那么2个算法都可以给出相同的结果；但对于非简单多边形，转角法则有很高的精度。传统观点认为射线法的效率较高，转角法的速度较慢。

本文主要针对实际工作中需要判别点与任意多边形的关系，特别是存在自相交与带岛等特例的情况，研究利用改进的转角法判别点与多边形的相对关系，实现算法并应用于实践。

2 转角法及其改进模型

2.1 转角法

转角法是对角度的积分算法［7］。为了使其具有普遍性，定义在二维平面中某个封闭曲线关于某点的环绕数wn。令C（u）＝（x（u），y（u）），0≤u≤1且C（0）＝C（1），是二维连续曲线，点P为不在C（u）上的点。令CP（u）＝C（u）－P为从点P到C（u）的矢量，且其单位方向矢量为W（u）＝CP（u）／｜CP（u）｜。则该式定义了一个连续的从曲线C到单位圆S1的映射，且 W（u）可以表示为 W（u）＝（cos（u），sin（u））。式中：（u）是正的逆时针方向的角。环绕数就等于W（u）环绕S1的次数的整数部分，可用式（1）表示：

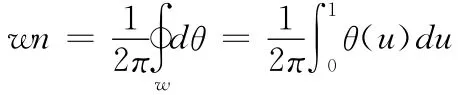
在处理任意点P与由顶点V1，V2，……，VN＝V0构成的多边形相对关系时，积分可以简化为计算带符号的角度的总和，这些角为PVi与PVi＋1的夹角。若i＝angle（PVi，PVi＋1），则有：

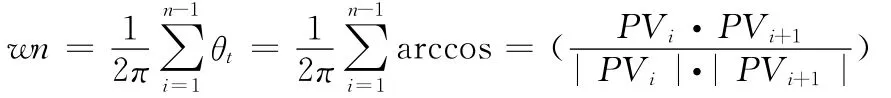
当代数和为0，则点P在多边形的外部，否则，点在多边形的内部或边界上。

2.2 改进的转角法

由于转角法中使用了非常耗时的arccos函数，故效率不高，改进的转角法可以克服该缺点。在S1中任取一点Q。由于曲线W （u）环绕，则其可能多次经过Q点。当W（u）按逆时针方向经过Q点时，记为＋1次；顺时针则记为－1次，则次数总和就是W环绕S1的次数，正好等于环绕数wn。以被检测点P为端点向Q方向延伸做一条射线R，则R穿越C的交点与W经过Q的点是一一对应的。当R从C的右边跨到左边时，该穿越数为正，记为＋1；反之为负，记为－1。当曲线C退化为多边形时，算法只需要对多边形C的每一条边做一次判断。对所有的边测试完后，将所有的穿越值加起来就是环绕数wn了。当wn为0时，点在多边形外；否则在多边形内［7］。

3 算法实现

改进的转角法不但具有与射线法相同的效率，且更加精确［7］。实现该算法的问题主要有2个，一是射线的穿越数正负判别，二是射线的选取。在讨论完这2个问题后，将算法进行具体实现，并与人工处理结果进行验证。

3.1 穿越数符号判别

判别穿越数的正负号时，可以通过曲线C的一个法线矢量与方向适量Q的数量积的符号来判断。当曲线C退化为多边形时，只需要对C的每一条边做一次判断。

在实际判别过程中，不需要计算射线与边的交点，只需要判别点P是否在边的左边。对于方向向上与方向向下的边的判别与是否在左边的规则不同。对于方向向上的边，如果穿越射线到达P的右边，则P在边ViVi＋1的左边（见图1）；对于方向向下的边，若穿越射线的正方向，则P在边 ViVi＋1的右边（见图2）。

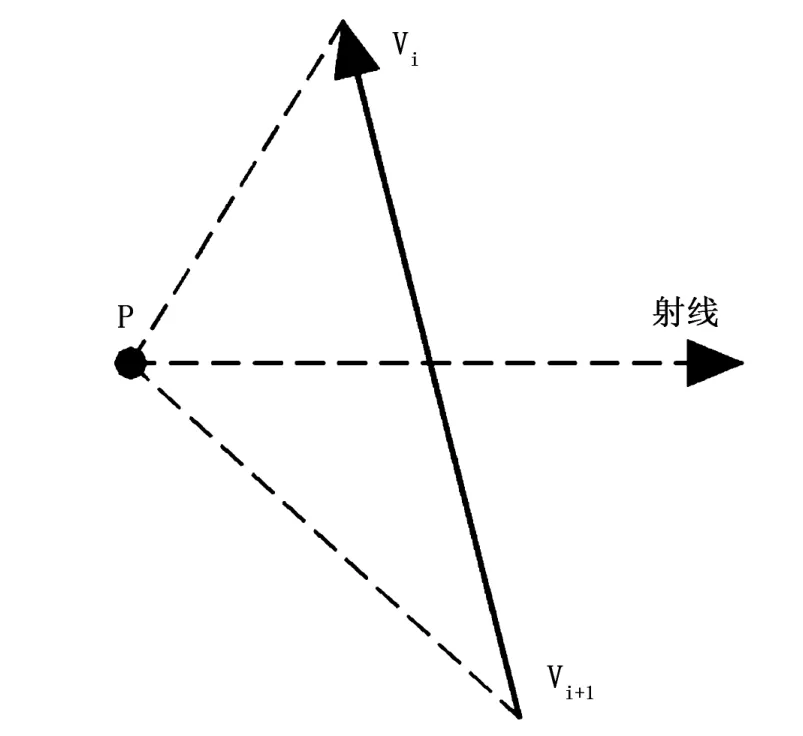
图1 方向向上的边判别图

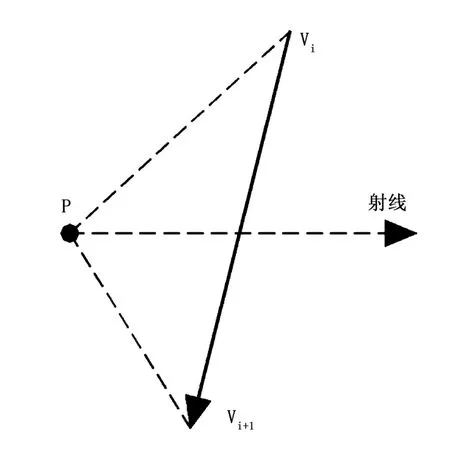
图2 方向向下的边判别图

3.2 射线选取

为了减少程序的计算量，常选取为一条向点P右边延伸且平行于X轴的射线。利用这条射线可以很容易地判别是否与多边形的边有交点。为了计算环绕数，算法简单地遍历多边形的所有边，测试是否穿越边及与穿越边的相对关系（左右侧），最后将环绕数求和，便可判断其对应关系。

3.3 算法实现

根据2.2节的改进算法，编制程序进行具体实现。判别点与多边形的相对关系时，为了提升程序的处理效率，在读取多边形的各条边的坐标数据后，先生成一个涵盖该多边形的最小矩形范围，然后再依次计算并保存多边形各条边的相关参数，降低程序计算量。在判别点与多边形的相对关系时，首先判别点是否处于最小矩形范围内，如果点不在该范围内，则不可能落在多边形内，可直接排除；利用2.2节算法，依次判别各个数据点与多边形各条边的相对关系，计算点的环绕数。若环绕数等于0，则该点在多边形的外部；否则，该点在多边形的内部，并对其进行标记。处理完所有的数据后，将结果保存到文件中。

3.4 算例验证

为了验证程序的正确性，采用象山港某航道1∶500的多波束测量数据进行测试。测试区域分为2个部分，第一部分为四边形，第二部分数据为任意多边形，其中数据格网间距为4m，共有425301个。如果采用人工方式在AutoCAD中进行筛选，由于数据量大、导入时耗时长、操作效率低，容易产生错漏。采用程序处理时，只需按照给定的格式分别编辑多边形角点坐标及测点数据，便可以得到筛选后的结果。分别将采用人工方式和程序自动筛选的数据放在一起进行比较，两者之间的结果基本一致，采用程序进行处理效率较高。