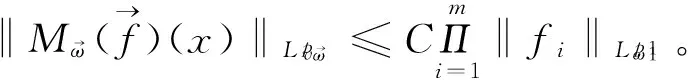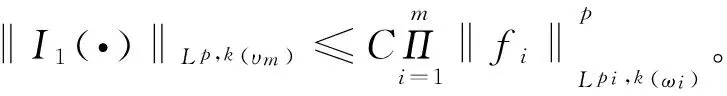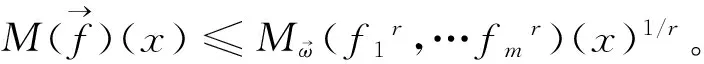多线性极大函数在加权Morrey空间中的有界性
2014-04-02饶贤清
喻 晓,饶贤清
(上饶师范学院,江西 上饶 334001)
引言及主要结论
1975年,Coifman和Meyer在[1]中首次引入了多线性C-Z理论。2002年,Grafakos和Torres在[2]中系统地研究了如下形式的多线性奇异积分算子:


定义1[3]如果一个局部可积函数ω(x)满足如下不等式:
其中1 另一方面,Morrey于1938年在[5]中引入了以其姓氏命名的Morrey空间Mp,λ,其定义为 在给出定理1的证明之前,我们先给出一些证明过程中需要的引理。 如果一个函数ω满足ω(2B)≤Cω(B),其中B为任一方体,C为和ω以及B无关的常数,则我们称ω满足倍测度条件,简记为ω∈△2。 引理1.1.[8]如果ω∈Ap(1 引理1.2.[8]如果ω∈△2,则存在大于1的常数C,使得ω(2B)≥Cω(B)。 引理1.3.[9]如果ωi∈Ar,r为大于1的实数,则对任意的B⊂Rn,我们有 这里C为一个和B无关的常数。 根据引理1.3,我们注意到如果ωi∈Ar(r>1),则我们有 (1.1) 引理2.3.假设0 其中C是一个和f无关的常数。 ∶=I1(x)+I2(x). 这里Σ′代表其通项中至少有一个α1不等于0。 首先我们给出I1(x)的估计。根据引理2.2,引理1.1以及 (1.1),我们有 接下来我们估计I2(x),首先我们考虑α1=α2=…=αm=∞这一情形。则对任意的x∈B=B(x0,R)以及B⊂3D,我们有 并且根据引理1.1以及1.2,有如下不等式: 于是根据(1.1),可得 故有 (2.1) 最后只需讨论的情形为:αi=αi+1=…=αj=∞,{αi,αi+1,…,αj}⊂{1,2,…,m}。不失一般性,我们仅仅考虑α1=∞,α2=α3=…=αm这种情形,因为其余的情形和这种情形类似。综合前面两种情况的估计过程,我们有 于是根据Holder不等式以及(1.1),有 (3.2) 定理1的证明:最后,我们将给出定理1的证明。由于ωi∈Ar,我们有 至此我们完成了定理1的证明。 参考文献: [1] Coifman R.,Meyer Y., On commutators of singular integrals and bilinear singular integrals[J]. Trans. Amer. Math. Soc., 1975,212:315-331. [2] Grafakos L., Classical and Modern Fourier Analysis[M].Prentice Hall (2004). [3] Muckenhoupt B., Weighted norm inequalities for the Hardy maximal function[J]. Trans. Amer. Math. Soc.1972,165:207-226. [4] Lerner A.K., Ombrosi S., Perez C. et al., New maximal functions and multiple weights for the multilinear Calderon-Zygmund theory[J]. Adv. Math., 2009,220:1222-1264. [5] Morrey C.B., On the solutions of quasi-linear elliptic partial differential euqations[J]. Tran. Amer. Math. Soc., 1938,43:126-166. [6] Komori Y.,Shirai S., Weighted Morrey spaces and a singular integral operator[J]. Math. Nachr., 2009, 282:219-231. [7] Wang H.,Yi W.T., Multilinear singular and fractional integral operators on weighted Morrey spaces[J].Funct. Spaces Appl., 2013, Article ID 735795. [8] Grafakos L., Torres R.H., Multilinear Calderon-Zygmund theory[J].Adv. Math.2002,165:124-164. [9] Xue Q.Y., Yan J.Q., Multilinear version of reversed Holder inequality and its applications to multilinear Calderon-Zygmund operators[J]. Math. Soc. Japan,2012, 64:1053-1069.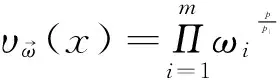
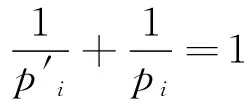
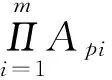



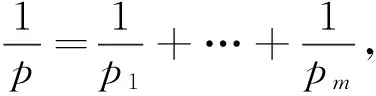
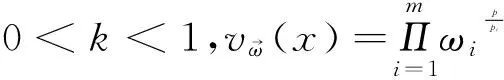
1 本文主要引理
2 定理1的证明