基于灰色系统理论的煤矿安全投入结构分析与优化
2014-04-02张飞燕
张飞燕,孟 薇,韩 颖
(1.河南理工大学安全科学与工程学院,河南 焦作 454000;2.河南理工大学能源科学与工程学院,河南 焦作 454000)
安全投入研究是一个新兴领域。如何对安全投资进行合理分配,以利用有限资源获取最大安全效果,实现最佳安全效益,是该研究领域关注的焦点问题。梁瑞等[1-2]采用偏相关分析和不变替代弹性生产函数分析方法,建立了安全投入与事故函数分析模型,并以某化工企业为例,进行了实例分析;李宏勋等[3]建立了安全投资-效益灰色关联分析模型,确定了某石化公司安全投资中各分项投资与效益的相关程度;施式亮等[4]依据安全工作的专业类型将安全投资划分为6个方向,选用灰色关联分析方法对某钢铁企业各方向安全投资与安全产出之间的关联度进行了排序比较,确定了各安全投资方向的重要程度;于志鹏等[5]采用线性变换及合理判定分辨系数的方法,提出了改进的模糊灰色关联分析法,对某石化公司安全投资因素与效益关系进行了分析;张杰等[6]提出了安全投入数量限度问题和安全投入的阈值,建立了安全效益评价模型和安全投入与安全指标的函数关系模型,对安全投入与安全水平、安全效益的关联关系进行了定性分析;董大旻等[7]借鉴欧洲质量卓越模型,建立了建筑企业安全投入绩效评估结构方程模型,并对安全投入构成要素之间的复杂交互影响关系进行了实证分析;王书明等[8]运用“流变-突变”理论对煤矿安全投入效果进行了分析,发现其随着时间的推移表现出“安全流变-突变”的特征。
综上所述,众多研究者就安全投入问题开展了大量卓有成效的研究工作,但其对煤矿领域涉及较少;而煤矿安全投入研究,对于提高煤矿安全投入产出效益、确保矿井安全生产具有重要意义。基于此,本文开展了基于灰色系统理论的煤矿安全投入结构分析与优化研究。
1 煤矿安全投入概述
煤矿安全投入是指煤炭企业为实现安全生产,在矿井设计、煤炭生产、经营过程中所消耗的人力、物力和财力的总和[9]。它是衡量煤矿安全活动消耗各种资源的重要尺度。
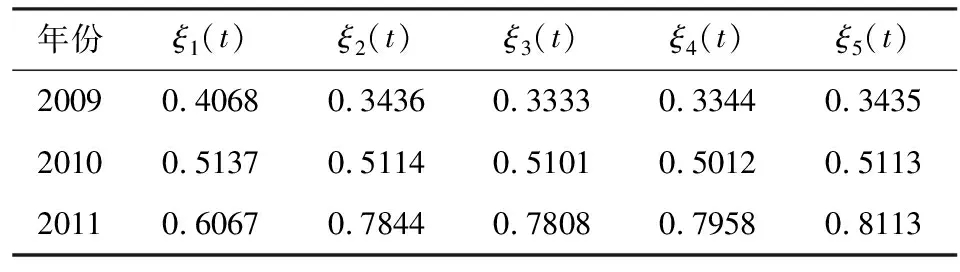
美国学者Votey提出了“投资-效益曲线”,如图1所示[10],可以看出:当安全投入R 图1 投资-效益曲线 关于安全投入分类,国内外研究者提出了多种方法。其中,梅强[11]将安全投入分为五类:①安全技术措施费:主要包括生产设备和设施的安全防护装置,生产区域安全通道与标志所需费用;②工业卫生措施费:主要包括生产环境有害因素治理以及为改善劳动条件的设施所需费用;③安全教育费用:从人的角度出发,为提高人的安全文化素质而进行书刊购买、安全宣传与展览、安全教育、安全培训等所需费用;④劳动保护用品费:为使生产人员在生产过程中远离危害,保护人身安全所必备的个体防护用品费;⑤日常安全管理费:企业安全管理部门办公费及其人工费用。上述五类内容与煤矿安全投入结构类似,故本文选用该分类方法展开研究。 安全投入各要素与安全效益之间的关系非常复杂。当安全投入结构发生变化时,安全效益随之变化,甚至会产生较大波动,两者构成一个不确定性系统。实践表明,灰色系统理论为研究此类问题的经典、有效工具,它以“部分信息已知、部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象,主要通过对“部分”已知信息的生成、开发,提取有价值的信息,实现对系统运行行为、演化规律的正确描述和有效监控[12]。 下面,对灰色系统理论的两种方法进行简要介绍。 灰色关联分析是灰色系统理论中的一种重要分析方法,其基本思路是:以各个序列在几何曲线上与目标值的接近程度、差异程度及发展态势,来确定各要素与目标值之间的相关程度并对其进行排序;曲线越接近,相应序列之间的关联度就越大,反之就越小[12]。 灰色关联分析步骤[12-13]如下所示 。 1)求各序列的初值像 i=0,1,2,…,m (1) 2)求差序列 Δi=(Δi(1),Δi(2),…,Δi(n), i=1,2,…,m (2) 3)求两极最大差与最小差 (3) 4)求关联系数 ξ∈(0,1),k=1,2,…,n; i=1,2,…,m (4) 5)计算关联度 i=1,2,…,m (5) 经典灰色关联分析方法着重从两条曲线之间的面积大小来度量两曲线的相似程度,忽略了曲线的变化趋势;而且没有考虑各因子的权重差异,即按等权重处理[14]但是,在工程实际中,各因素的权是不同的,必须考虑权重的差异,故本文引入加权灰色关联分析方法。 加权灰色关联分析步骤[14]如下所示 。 设X={xσ|σ=0,1,2,…,m}为序列关联因子集,x0为参考函数(母因素),xi为比较函数(子因素),xσ(k)为xσ在第k点的值,其中k=1,2,…,n。 设x′=(x′(1),x′(2),x′(3),…,x′(n))为序列x=(x(1),x(2),x(3),…,x(n))的累减生成序列,其中x′(1)=x(1),x′(k)=x(k)-x(k-1),(k=2,3,…,n)。 对于x0、xi,令 (6) 式中,λ1、λ2分别为位移加权系数、变化率加权系数,一般均取0.5;ε为分辨系数,取为0.5。 灰色加权关联度为 γi=γ(x0,xi)= (7) 式中,βk为因子k常态化的权重系数,通过白化权函数法确定,方法如下所示。 设白化权函数为 f(x)=xe1-x+(1-x)ex-1 (8) 已知序列:xi(k)=(xi(1),xi(2),…,xi(k),…,xi(n)),(i=1,2,…,m;k=1,2,…,n) 1)求各序列中各属性因子总和 (9) 2)求因子熵 (10) 3)求熵总和 (11) 4)求相对权重 (12) 5)利用正规化法求各因子权重 (13) 基于对某煤矿安全投入情况的调研分析,得出该矿2009~2011年的五项安全投入及事故经济损失,见表1。需要说明的是,依据海因里希对超过5000例伤亡事故的经济损失统计分析结论[15],直接经济损失与间接经济损失比例为1∶4,即伤亡事故的总经济损失为直接经济损失的5倍。 表1 某煤矿安全投入及事故经济损失统计结果/万元 安全效益包括减损、增值两部分,由于增值部分统计难度较大,本文采用减损数据,即总经济损失作为安全效益,记为X0(t);各分项安全投入记为Xi(t),i=1,2,…,5。 1)求各序列的初值像 由式(1),得出 2)求差序列 由式(2),得出 Δ01=(0,0.56,0.09), Δ02=(0,0,0.08), Δ03=(0,0.07,0.20), Δ04=(0,0.37,0.85), Δ05=(0,0.07,0.12) 3)求两极最大差与最小差 由式(3),得出 M=0.85,m=0 4)求关联系数 由式(4),取ξ=0.5,得出 γ01(1)=1,γ01(2)=0.43,γ01(3)=0.83 γ02(1)=1,γ02(2)=1,γ02(3)=0.84 γ03(1)=1,γ03(2)=0.86,γ03(3)=0.68 γ04(1)=1,γ04(2)=0.54,γ04(3)=0.33 γ05(1)=1,γ05(2)=0.86,γ05(3)=0.78 5)计算关联度 由式(5),得出 γ01=(γ01(1)+γ01(2)+γ01(3))/3=0.75, γ02=0.95,γ03=0.85, γ04=0.62,γ05=0.88 对关联度进行排序,得:γ02>γ05>γ03>γ01>γ04,即:各分项安全投入对安全效益的影响程度由高到低依次为:工业卫生措施费、日常安全管理费、安全教育费用、安全技术措施费、劳动保护用品费。 根据加权灰色关联分析原理,可以得出 根据式(6)计算关联系数ξi(t),结果见表2。 表2 灰色关联系数 由式(9)可得 D1=4756.368,D2=975.47,D3=311.76, D4=747.361,D5=1137.46 由式(10)可得 由式(8),运用MATLAB软件计算白化权函数,得 由式(11)可得熵总和:E=0.8087 由式(12)可得相对权重为:λ1=0.1367,λ2=0.1768,λ3=0.2093 由式(13)可得各因子权为:β1=0.2615,β2=0.3382,β3=0.4003 由式(7)可得各因子的加权灰色关联度为:γ01=0.5230,γ02=0.5769,γ03=0.5723,γ04=0.5755,γ05=0.5875 对关联度进行排序,得:γ05>γ02>γ04>γ03>γ01,即:各分项安全投入对安全效益的影响程度由高到低依次为:日常安全管理费、工业卫生措施费、劳动保护用品费、安全教育费用、安全技术措施费。 根据表1,以年份为横坐标,分别以总经济损失、各分项安全投入为纵坐标绘图,如图2所示。需要说明的是:为了图形的整体效果及美观,对部分数据进行了处理,安全技术措施费除以3,总经济损失除以10,但这并不影响曲线的总体走势。 图2 直观分析曲线 由图2可以看出,按照各分项安全投入曲线与总经济损失曲线接近程度高低排序为:日常安全管理费、工业卫生措施费、劳动保护用品费、安全教育费用、安全技术措施费。 加权灰色关联分析结果与直观分析结果一致,但灰色关联分析结果与之有所偏差,原因在于:式(4)只含有反映两曲线接近程度的局部参数,而缺少反映两曲线接近程度的整体参数;式(6)则弥补了式(4)的不足,用序列的一次累减生成来描述曲线的变化趋势,从而有效反映了两曲线接近程度的整体参数。由此可知,加权灰色关联分析方法更适于工程实际应用。 根据加权灰色关联分析结果,某煤矿安全投入的重点应放在日常安全管理费上,其他四项安全投入也应依据其重要度,分项量化投入。 1) 本文将灰色系统理论引入煤矿安全投入研究中,分别运用灰色关联分析方法、加权灰色关联分析方法,对某煤矿安全投入结构进行了分析与优化,得出了各分项安全投入对安全效益的影响程度排序;依据直观分析结果,对两种方法进行了对比,结果表明,加权灰色关联分析方法更适于工程实际应用。 2) 安全投入结构分析与优化为煤矿企业合理分配安全投资提供了定量依据,对于指导企业科学决策、提升安全效益、实现企业效益最优化具有重要意义。 [1] 梁瑞,郭洪燕,姜峰.安全投入各要素分配方向的研究[J].中国安全科学学报,2010,20(7):128-133. [2] 梁瑞,郭洪燕,郭晓璐.安全投入模型的研究[J].中国安全科学学报,2011,21(1):32-36. [3] 李宏勋,郭伟光.安全投资-效益的灰色关联分析[J].中国石油大学学报:自然科学版,2005,29(6):131-134. [4] 施式亮,刘莉君,曹休宁,等.基于灰色系统理论的安全投资方向优化分析[J].中国安全科学学报,2007,17(4):62-66. [5] 于志鹏,陆愈实.模糊灰色关联法在分析安全投资因素与效益关系中的应用[J].中国安全科学学报,2007,17(3):62-66. [6] 张杰,苗金明,周心权,等.安全生产效益的分析评价及其与安全投入的关系[J].中国安全科学学报,2009,19(3):49-54. [7] 董大旻,冯凯梁.基于EFQM的建筑企业安全投入绩效评估SEM[J].中国安全科学学报,2012,22(2):10-16. [8] 王书明,何学秋,王恩元.基于“流变-突变”理论的安全投入决策[J].中国安全科学学报,2009,19(11):46-51. [9] 郑爱华.煤矿安全投入规模与结构分析及政府安全分类监管研究[D].徐州:中国矿业大学,2009. [10] 冯杰,李思义,张发明.以安全经济学原理探讨煤矿事故的控制途径[J].煤矿安全,2000(9):48-50. [11] 梅强.安全投资方向决策的研究[J].中国安全科学学报,1999,9(5):42-47. [12] 刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].第5版.北京:科学出版社,2010. [13] 邓聚龙.灰色系统基本方法[M].第2版.武汉:华中科技大学出版社,2005. [14] 罗佑新,张龙庭,李敏.灰色系统理论及其在机械工程中的应用[M].长沙:国防科技大学出版社,2001. [15] 吴穹,许开立.安全管理学[M].北京:煤炭工业出版社,2002.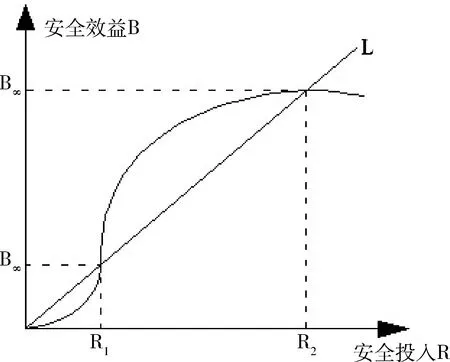
2 本文研究方法
2.1 灰色关联分析方法
2.2 加权灰色关联分析方法
3 实例分析

3.1 灰色关联分析结果
3.2 加权灰色关联分析结果

3.3 两种方法分析结果对比

4 结论
