基于纹理结构异常的织物疵点检测算法研究
2014-04-01,,,,
,,, ,
(中原工学院,郑州 450007)
在纺织工业生产中,疵点检测是质量控制的关键环节。据统计,二等布匹的价格是一等布匹的45%~65%。然而,目前疵点检测主要依靠人工检测,这是一项繁重和重复的工作。由于长时间工作,工人出现错误不可避免,而且只能检测出主要疵点的60%~75%[1]。因此,织物疵点的自动检测是一个研究热点。
织物疵点的检测可以分为基于统计的织物疵点检测方法、基于模型的织物疵点检测方法、基于时频谱分析的织物疵点检测方法等。基于统计的织物疵点检测是利用纹理分析技术进行疵点检测的方法,通过对织物纹理的分析可以获取相应的纹理特征(在提取灰度纹理特征时可以利用灰度共生矩阵[2]、子块的均值和方差[3]、子块的互相关函数[4]和K-L变换[5]),利用此特征来检测疵点区域;基于模型的织物疵点检测方法是将纹理建模看成一个随机过程,纹理图像则可以看成在图像空间上由这个随机过程产生的样本。Cohen F S等[6]利用高斯马尔科夫随机场模型来描述织物纹理,织物疵点检测过程则可以看作是来自该模型统计数据中的假设——检验问题;基于时频谱分析的织物疵点检测方法主要是针对具有均匀纹理的织物图像进行疵点检测的,将织物图像变换到频域时,织物纹理由一些基本的纹理基元按照周期性规则构成,纹理基元的周期性有利于疵点检测。例如Kumar A等利用Gabor滤波器组来进行疵点检测[7],Chan C利用Fourier分析对几类简单织物进行疵点检测[8],Ngan H Y T等利用小波变换对有花纹的织物疵点进行检测[9],该方法被认为是织物疵点检测的有效、可靠的方法,因为它适合分析局部特征[10]。然而,这些方法只能分析几种特定疵点,且缺乏灵活性,计算较复杂。
疵点检测方法由纹理分割和识别两个过程组成,之所以能检测出疵点位置是由于织物中疵点处的纹理结构与正常织物不同。正常织物的纹理结构是按一定规律排列的,像素之间表现出高的相似性,而疵点会破坏这种规律性,导致纹理结构的异常,且疵点的灰度与正常织物的灰度差异较大,故可以通过织物纹理结构特征的异常信息判断疵点的位置。基于此,本文提出了一种基于纹理结构异常的织物疵点检测算法。
1 邻域结构图
为了充分利用具有大量重复模式的纹理图像中的高冗余性,本研究提取了织物纹理的全局特征。通常情况下,冗余性越高意味着不同像素之间的灰度越相似。如果比较给定像素i与其局部邻域(该局部邻域称为搜索窗Si)内其他像素灰度的相似性,则可以得到像素i的邻域相似性,那么纹理图像中的高冗余性意味着图像中大部分像素的邻域相似性是相同的。利用以像素i和像素j为中心,大小为r×r的方形局部邻域窗Ni和Nj之间的欧式距离来定义给定像素i和j之间的不相似性,即
(1)
式中:i为当前考虑像素,且位于Si的中心;j代表在搜索窗Si内与像素i相邻的所有其他像素;v(Ni)为像素i周围邻域像素值的向量。之所以采用像素邻域灰度的欧式距离,而没有采用单个像素值之间的差值,主要是为了降低随机噪声对像素相似性的影响。
把在给定像素处产生的邻域相似性被定义为该像素的邻域结构图(NSM, Neighborhood Structure Map)。邻域结构图度量了给定像素与搜索窗中邻域像素之间的相似性程度。由式(1)所得的值越小,则邻域像素与中心像素越相似。由于疵点破坏了织物纹理结构的规律性,因此,疵点区域像素的邻域相似性与正常区域像素的邻域相似性有较大区别。为了检测出织物图像中的疵点区域,需要计算能代表正常区域的主邻域结构图(此主邻域结构图代表了该织物纹理的结构特征),然后通过比较每个像素的邻域结构图与主邻域结构图的差异来判断该像素的显著性,最后通过分割算法分割出疵点区域。
2 主邻域结构图
鉴于织物纹理图像中的高冗余性,图像中大部分像素的邻域结构图是相同或相似的。可以在一些具有代表性的邻域结构图中提取纹理图像的全局特征,即主邻域结构图(DNS Map,Dominant Neighborhood Structure Map)。通过简单的步骤可以获得织物纹理的主邻域结构图:首先,使用式(1)计算搜索窗Si中所有像素与搜索窗中心像素i的相似性,获得邻域结构图;其次,确定用于构建主邻域结构图的像素之间的空间间隔;最后,计算像素邻域结构图的平均值作为主邻域结构图,即
(2)
式中,NSM(i)代表第i个像素的邻域结构图,N为所选像素的个数。
搜索窗和邻域窗的大小是影响主邻域结构图计算时间的2个重要参数,它们的最佳值可以通过实验获得,依据经验本文将其分别设置为15×15和7×7。为了减少生成主邻域结构图所需要的计算量,利用织物纹理图像的一个重要属性,即内在冗余性或全局一致性。织物纹理图像的全局一致性在不同分辨率下都存在并且相同,这就意味着可以在不同分辨率下获取纹理图像的主邻域结构图,像素之间的空间间隔是影响主邻域结构图的又一个重要因素。在给定分辨率下,为了生成主邻域结构图,需要有足够数量像素的邻域结构图,所选择的像素具有一定的空间间隔且覆盖整个织物纹理图像。通过试验发现,具有代表性的主邻域结构图可以通过纹理图像像素的一个小的子集来获取,其中子集的大小与图像尺寸和像素空间间隔有关,且纹理图像中所选择相邻像素的搜索窗之间必须相互重叠,将所选择像素的所有邻域结构图的平均值作为主邻域结构图。对于平滑一致且具有重复模式的纹理图像,由于其冗余性,大部分像素的邻域结构图之间差异极小,所以选定像素的邻域结构图的平均值便能代表所有单个像素的邻域结构图,主邻域结构图近似代表纹理图像的全局纹理特征。
3 疵点图像分割
本文采用迭代最优阈值分割方法对显著图进行处理,实现对织物疵点区域的检测与定位。该方法是通过一个初始阈值将图像分为疵点和背景两部分,分别计算它们的灰度均值,再以灰度均值的平均值作为新阈值,并对图像进行再次分割,直到两次分割所得阈值的差小于设定值。主要步骤如下:
(1)计算初始阈值T0={Tk|k=0}
(3)
其中,Zmin、Zmax分别表示图像中像素的最小和最大灰度值。
(2)利用阈值Tk把图像分割成两个区域R1和R2
R1={f(i,j)|f(i,j)≥Tk}
(4)
R2={f(i,j)|0≤f(i,j) (5) 其中,f(i,j)是像素(i,j)的灰度值。 (3)计算R1和R2的灰度均值Z1和Z2 (6) (7) 其中,N(i,j)是像素(i,j)点的权重系数。 (4)选择新的阈值Tk+1 (8) (5)如果Tk+1-Tk<δ(δ为设定值),则结束;否则k=k+1,转至步骤(2)。 (6)利用步骤(5)中求出的最优阈值,对图像进行分割,将其分为疵点和背景两部分。 织物图像的疵点区域相对于正常区域来说是极小的。根据上述获取纹理图像主邻域结构特征的方法,认为一幅有缺陷织物图像的主邻域结构仍然可以代表正常织物纹理的特征。基于正常区域像素点的邻域结构图与主邻域结构图相差不大,而疵点区域像素点的邻域结构图却明显不同于主邻域结构的现象,本文把像素点的邻域结构图与主邻域结构图的差异定义为该像素的显著性,并采用上述分割方法对显著图进行分割。基于全局主邻域结构特征的织物缺陷检测算法流程图如图1所示。 (1)由图像大小和像素空间间隔确定主邻域结构像素的数目。 (2)根据式(1)计算像素的邻域结构图。 (3)计算纹理图像的主邻域结构图(主邻域结构图是所选择像素的邻域结构图的平均值,见式(2))。 (4)获取显著图:对于像素i,计算其邻域结构图,然后将该像素的邻域结构图与主邻域结构图的绝对差值作为该像素的显著性值,进而得到所有像素的显著性值,即织物疵点图像显著图。 图1 基于全局主邻域结构特征的织物缺陷检测算法流程图 (5)显著图分割:将获得的显著图采用迭代阈值分割方法得到二值图像,图像中白色区域代表疵点。 为了验证算法的有效性,本文在织物图像库中选择几类常见的疵点图像(包括漏纱、破损、纬松、跳花等)用于试验,图片大小为256×256。疵点图像如图2所示,从图2可以看出图2(b)中带花纹图像虽然定了疵点位置,但大小与实际疵点稍有差别,是因为纹理背景较复杂,部分疵点相对正常区域不够显著,在分割时被认为是正常区域;对于其他的各类疵点,本方法均准确检测出了疵点,并且准确分割出疵点位置。 原始织物图 对应的显著图 对应的分割图 本文利用像素的邻域结构图与主邻域结构图的差异来计算像素的显著度,疵点区域的邻域结构图与主邻域结构图差别明显,从而有效地突出了疵点区域。通过试验发现,本文提出的方法为复杂纹理的织物图像建立了有效的显著图,突出了疵点区域;后续的迭代阈值分割实现了对疵点区域的有效检测及定位。此方法为背景复杂的目标检测提供了一种新思路。 参考文献: [1] Schicktanz K. Automatic Fault Detection Possibilities on Nonwoven Fabrics[J]. Melliand Textiberichte, 1993,74: 294-295. [2] Tsai I S, Lin C H, Lin J J. Applying an Artificial Neural Network to Pattern Recognition in Fabric Defects[J]. Textile Research Journal, 1995, 65(3): 123-130. [3] Zhang Y F, Bresee R R. Fabric Defect Detection and Classification Using Image Analysis[J]. Textile Research Journal, 1995, 65(1): 1-9. [4] Wood E J. Applying Fourier and Associated Transforms to Pattern Characterization in Textiles[J]. Textile Research Journal, 1990, 60(4): 212-220. [5] Unser M, Ade F. Feature Extraction and Decision Procedure for Automated Inspection of Textured Materials[J]. Pattern Recognition Letters, 1984, 2(3): 185-191. [6] Cohen F S, Fan Z, Attali S. Automated Inspection of Textile Fabrics Using Textural Models[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(8): 803-808. [7] Kumar A, Pang G K H. Defect Detection inTextured Materials Using Gabor Filters[J]. IEEE Transactions on Industry Applications, 2002, 38(2): 425-440. [8] Chan C, Pang G K H. Fabric Defect Detection by Fourier Analysis[J]. IEEE Transactions on Industry Applications, 2000, 36(5): 1267-1276. [9] Ngan H Y T, Pang G K H, Yung S P, et al. Defect Detection on Patterned Jacquard Fabric[C]//Proceedings of the 32nd Applied Imagery Pattern Recognition Workshop. Britain:Computer Society IEEE, 2003: 163-168. [10] Jasper W J, Garnier S J, Potlapalli H. Texture Characterization and Defect Detection Using Adaptive Wavelets[J]. Optical Engineering, 1996, 35(11): 3140-3149.4 织物疵点检测
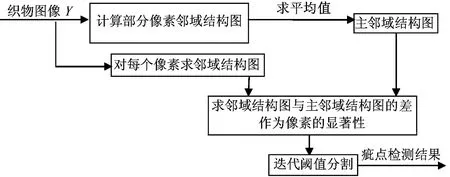
5 试验结果分析



6 结 语
