北京市PM10浓度变化规律的小波分析

， ，

(1.中原工学院，郑州 450007; 2.河南省计量科学研究院，郑州 450008；3.中国矿业大学(北京)，北京 100083)

城市大气可吸入颗粒物污染已经成为大气科学研究的热点问题[1].通过对可吸入颗粒物浓度变化的分析，可以深入了解可吸入颗粒物污染的来源、变化规律及影响因素，从而采取有针对性的措施[2-3].受污染源、气象条件等多种因素的影响，实际监测出的颗粒物污染物浓度时间序列数据有很大的无规律变化，其中有许多是由于偶然因素造成的，这些偶然因素变化严重影响其变化规律及变化原因的分析[4].消除由于偶然因素变化造成的影响，分析污染物浓度的真实变化规律，从信号处理的角度来看是典型的去噪处理[5].小波分析技术出现后,已经有一些研究用小波分析方法对大气污染物的时间序列进行去噪处理，取得了不错的效果[6-7].本文采用MATLAB小波分析对PM10质量浓度时间序列数据进行去噪处理,分析了去噪处理的具体过程，并对北京市2010-2011年度PM10质量浓度随时间变化的数据进行了小波去噪分析.

1 时间序列数据小波去噪处理的原理

1.1 时间序列数据的去噪处理

信号处理时，一般认为低频信号是有用信号而把高频信号看作噪声，要求有用信号和噪声的频谱相互分开[5,8-9].

对时间序列数据去噪的传统方法主要有移动平均法、传统滤波方法、卡尔曼滤波方法和维纳滤波方法[10].传统滤波方法的傅里叶(Fourier)变换是将时域信号变换到频域，但由于傅里叶变换中采样间隔都是常数，时间域与频率域之间彼此是整体刻画，不能用于局部分析，难以实现信噪的有效分离[11].

小波分析(或小波变换)具有自适应性质和数学显微镜性质,与传统的傅里叶变换相比，能够提供信号在时-频域上的局部化特征，特别适合非平稳、非线性信号的处理[10].将小波变换用于信号去噪，能在去噪的同时不损坏信号的突变部分，是一种对信号的局部频谱进行分析的比较理想的数学工具[12].

1.2 小波去噪处理的MATLAB实现

小波阈值消噪法是小波消噪方法中应用较广泛的一种方法,它具有方法简单、计算量小、去噪效果好的特点.小波阈值消噪的主要理论依据为:属于空间的信号在小波域内的能量主要集中在有限的几个系数中,而噪声的能量却分布于整个小波域内,因此经过小波分解后得到小波变换系数m,信号的小波变换系数要大于噪声的小波变换系数,于是可以找到一个合适的数作为阈值(门限) ,当m小于阈值时,认为这时的m主要是由噪声引起的;当m大于该阈值时,认为这时的m主要是由信号引起的,从而实现了信噪分离[12].

MATLAB将矩阵运算、数值分析、图形处理、编程技术等功能有机地结合在一起，具有强大的数学计算和分析功能、丰富的可视化图形表现功能和方便的程序设计能力[13].

MATLAB中实现小波去噪功能的常用函数是wden[14],格式为:

[XD,CXD,LXD] = wden(X,TPTR,SORH,SCAL,N,′wname′)

式中：X是原始时间序列信号；TPTR表示阈值选择的原则；SORH表示选择软阈值或硬阈值处理方法；SCAL表示小波分解时定义所用的阈值是否需要重新调整；N表示小波分解的层次；′wname′是所使用的正交小波名称；XD、CXD、LXD分别是在上述参数作用下小波去噪后得到的信号及其附加小波分解结构.

2 MATLAB小波去噪函数参数及其选择

在对PM10进行小波分析时,wden函数的参数选择对去噪的结果有直接影响,现就不同参数对PM10时间序列去噪结果的影响分析如下：

2.1 阈值的几种选择原则

在MATLAB中有4 种阈值函数形式可以选用:rigrsure采用Stein的无偏似然估计原理进行自适应阈值选择;sqtwolog表示采用固定的阈值形式; minimaxi表示采用极大极小原理选择的阈值,它和sqtwolog一样，也是一种固定的阈值, 它产生一个最小均方误差的极值; heursure表示选择启发式阈值, 它是sqtwolog 和rigrsure 的综合.具体的阈值公式可参考文献[15].

rigrsure和minimaxi阈值选取原则较为保守(仅将部分系数置为零),可以将弱小的信号提取出来[15].通过对PM10的时间序列变化规律分析,并经试验发现,几种选择原则没有太大区别.本文选取rigrsure作为阈值选取原则.

2.2 软阈值和硬阈值

在对小波系数作门限阈值处理操作时, 硬阈值处理只保留较大的小波系数并将较小的小波系数置零,软阈值处理将较小的小波系数置零但对较大的小波系数向零作了收缩.经试验发现,本文分析的情况软、硬阈值选择没有太大区别.本文选取软阈值作为阈值处理方法.

2.3 阈值调整

SCAL参数定义所用的阈值是否需要重新调整,有3种情况：scal=′one′不进行重新估计; scal=′sln′只根据第一层小波分解系数估计噪声水平;scal=′mln′在每个不同的小波分解层次估计噪声水平. 图1是对PM10进行小波分解时用不同阈值重新调整方法得出的不同结果,使用函数为wden(X,′rigrsure′,′s′,SCAL,5,′sym8′).可以看出,对PM10进行小波分解时应该选择′one′.

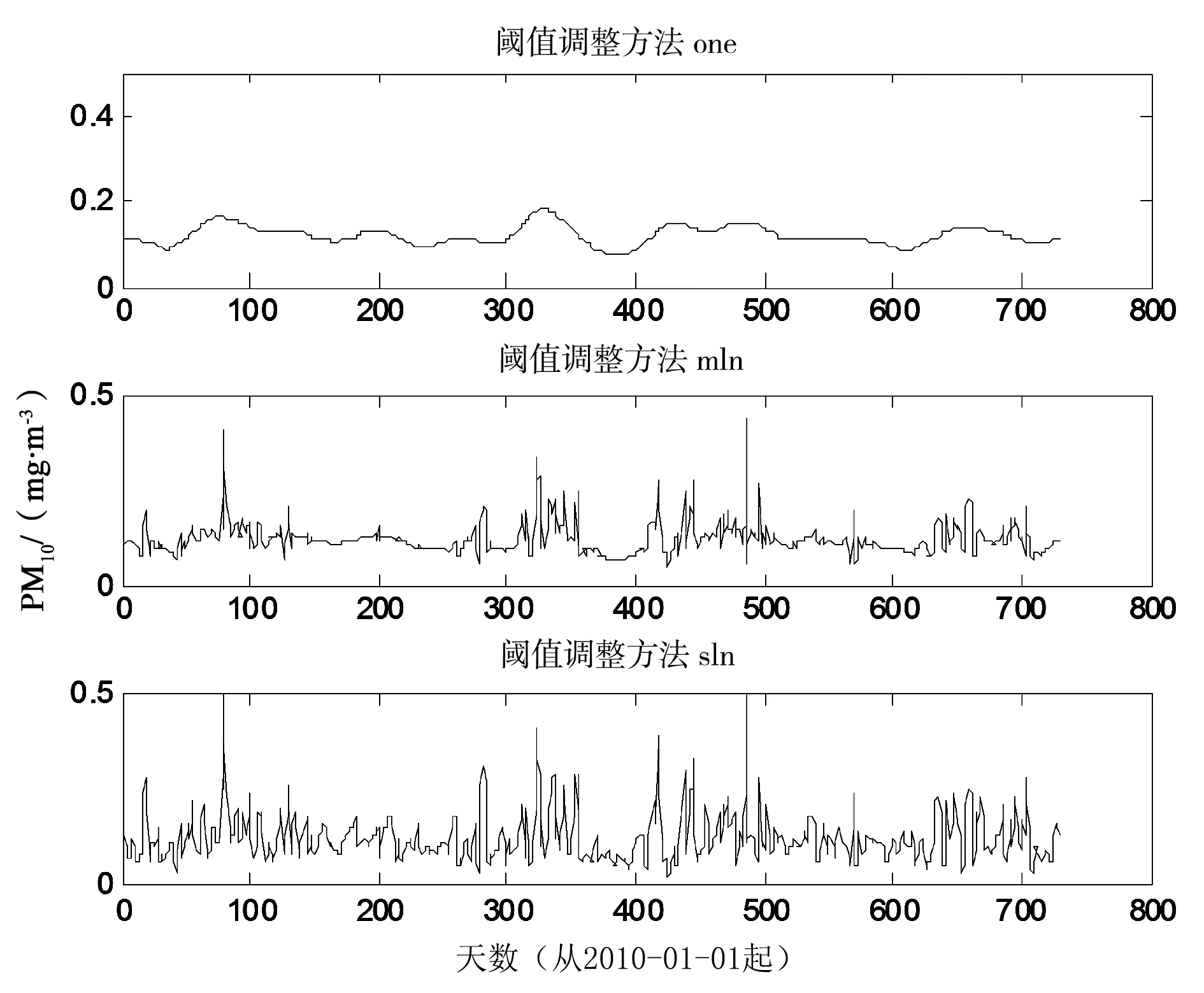
图1 不同阈值重新调整方法对去噪结果的影响

2.4 分解层次的比较

图2是采用不同分解层次的PM10小波去噪效果图,使用函数为wden(X,′rigrsure′,′s′,′one′,level,′sym8′).从图中可以看出，随着小波分解层次的增加，去噪效果变好.但是分解层次增加到5层以上后去噪效果改善已经不明显.本研究分解层次取5层.

2.5 小波函数的选取

图3是采用不同小波函数的PM10小波去噪效果图,使用函数为wden(X,′rigrsure′,′s′,′one′,5,wname).小波函数(wname)可以从Daubechies (dbN)、symlets(symN)等常用的小波函数中选取一个正交小波,从图中可以看出，小波函数Daubechies和symlets同层次的去噪效果基本相同,随着小波函数序数的增加,去噪效果较好.本文选择sym8作为去噪小波函数.

3 实例分析

根据国家环境保护部网站公布的北京市2010-2011年度大气空气质量监测结果，将用污染指数表示的当天的可吸入颗粒物的污染情况转换为质量浓度值,具体转换方法见文献[16]，其中部分缺省数据根据前后两天线性插值得到.

将北京市2010-2011年度PM10质量浓度数据导入MATLAB，对数据进行小波去噪分析，北京市2010-2011年度PM10质量浓度随时间的变化曲线和小波分析结果如图4所示.图5是按月份平均的柱状图.可见，经过小波分析去噪后，污染物的变化规律比较明显地显现出来了，小波去噪处理在分析时间序列数据中确实有明显的效果.

从图4中PM10浓度变化可以看出，北京市PM10浓度变化在一年中呈现一定的规律性，每年年初有一下降的过程，随后又有上升，4、5月份开始下降，在7月份有一小峰值，随后逐渐下降，一般到8、9月份达到一年中的低点，随后逐渐上升到11月份达到较高值，以后逐渐下降到次年.分析可知，造成这种变化的原因,除了造成颗粒物污染的工业生产等活动的季节性波动外,也与影响颗粒物污染的气候气象条件及人类活动有关.每年的3-4月份，PM10浓度较高，这可能和春季的沙尘入侵有关，此时北京市气温逐渐升高,土壤解冻,风力较大,植被尚未完全长出,容易形成沙尘天气,造成颗粒物浓度较高; 随后风力变小,植被完全恢复,对抑制沙尘天气形成有利; 7月份是北京市的雨季，天气温度较高,风力较弱(表1所示的北京市1971-2000年的气候值)，空气的扩散能力减小，造成污染物积累，同时大量排放的机动车尾气在高温和强烈紫外线作用下发生二次反应，会生成较多的细颗粒物，这些因素都有可能使颗粒物浓度增加[17]；9月份秋高气爽,风力增加，污染物得以扩散,是一年中空气质量最好的月份；进入10月份后，温度降低，风力较小,雾天和逆温天气出现较多,同时降水减少，由降水造成的颗粒物清除减少，造成污染物积累，大气颗粒物浓度开始增加；到年底PM10浓度开始降低，主要原因可能是进入冬季后，冷空气频繁入侵，使颗粒物得到扩散、净化，同时北京冬季天寒地冻,局地土壤不容易被风吹起,使颗粒物浓度降低.

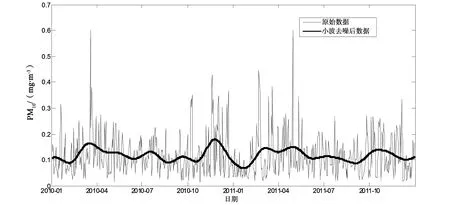
图4 北京市2010-2011年度PM10浓度随时间变化曲线和小波去噪结果

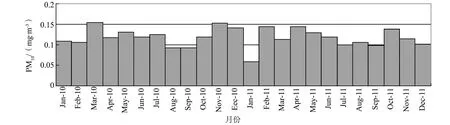
图5 北京市2010-2011年度PM10月平均变化图

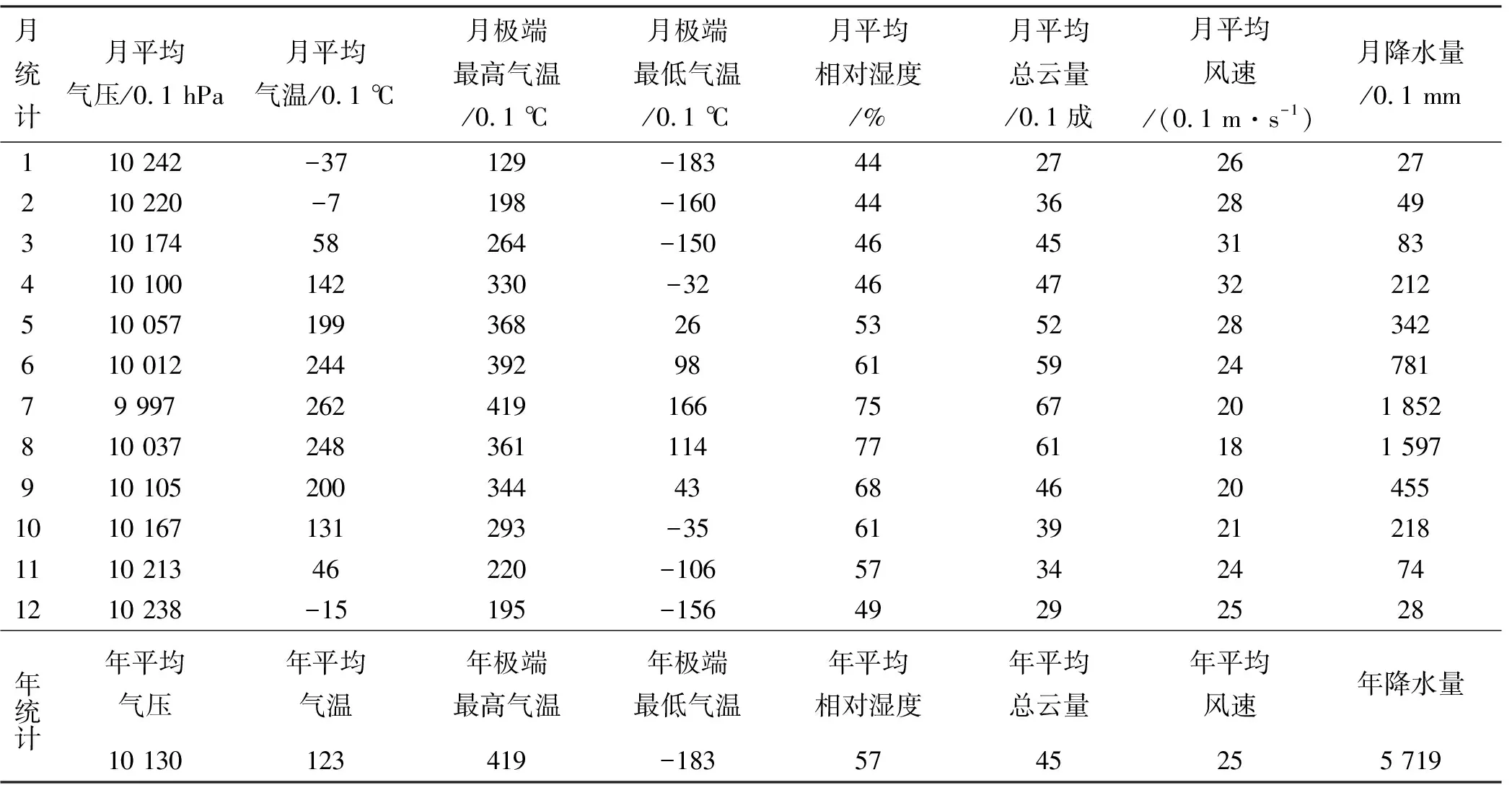
表1 北京市标准气候值(1971-2000年)

分析北京市大气污染物质量浓度的变化情况,不难看出，大气污染物浓度的影响因素非常复杂，不同年份相同月份的变化有所差异，如2011年1月份PM10污染特别小，而2月份PM10较高,这主要是由于1月冷空气频繁,有利于大气污染物的清除和扩散，且恰遇农历春节放假,工业排放和机动车尾气排放减少,而2月16日至24日，出现了典型的静风稳定天气，逆温较强，湿度上升，有时有雾，污染物易积累、难扩散，空气质量转差[17]，这与北京所处的地理位置和自然环境有关，也和气候、气象条件有关.总的说来，北京市大气质量较好的季节在5-10月份.

4 结 语

(1)小波去噪分析方法能较好地用来分析PM10的时间序列变化规律，可以消除偶然因素对大气颗粒物浓度变化的影响，更好地显示PM10的时间变化规律.

(2)在运用MATLAB提供的小波去噪分析函数时，不同参数对小波去噪的效果有不同的影响，应该根据时间序列数据的特点进行选择，以达到较好的去噪效果.

(3)对北京市PM10质量浓度数据进行小波去噪分析表明，北京市PM10浓度在一年中变化呈现一定的规律性，造成这种变化的原因除了造成颗粒物污染的工业生产等活动的季节性波动外,也与影响颗粒物污染的气候、气象条件及人类活动有关.

参考文献：

[1] Buseck P R，Posfai M. Airborne Minerals and Related Aerosol Particles: Effects on Climate and the Environment [J].P. Natl. Acad. Sci., 1999, 96:3372-3379.

[2] 孙杰，高庆先，周锁铨.2002年北京PM10时间序列及其成因分析[J].环境科学研究, 2007, 20 (6) : 83-86.

[3] 王宏，林长城，蔡义勇,等.福州市PM10突变特征与气象条件的关系研究[J]. 热带气象学报, 2008, 24(5): 564-568.

[4] Li S T, Shu L Y. Data Mining to Aid Policy Making in Air Pollution Management[J]. Expert Systems with Applications, 2004, 27(3): 331-340.

[5] 张燕, 杨洋.基于小波分析的金融时间序列消噪方法及应用[J].宁波大学学报(理工版), 2010, 23 (3): 56-59.

[6] 王海鹏，张斌，刘祖涵，等． 基于小波变换的兰州市近十年空气污染指数变化[J]． 环境科学学报，2011, 31(5): 1070-1076.

[7] 陈柳,马广大.小波变换在大气污染物时间序列分析中的应用[J].西安科技大学学报, 2006, 26(1): 58-61.

[8] 钱舒. 小波在股市数据分析中的应用[J]. 经济数学, 2002, 19(4): 80-84.

[9] Sang Y, Wang D, Wu J, et al. Entropy-Based Wavelet De-noising Method for Time Series Analysis[J].Entropy, 2009, 11:1123-1147.

[10] De Gooijer J G，Hyndman R J. 25 Years of Time Series Forecasting[J]. International Journal of Forecasting, 2006, 22: 443-473.

[11] 张典,蒋勇军,杨平恒,等.岩溶地下河水文时间序列小波消噪处理[J].人民长江, 2009, 40(21): 45-46.

[12] 范晓志. 小波变换的信号去噪应用[J]. 武汉科技大学学报(自然科学版), 2004, 27(3): 286-288.

[13] 李海涛，邓樱.MATLAB程序设计教程[M].北京：高等教育出版社，2002.

[14] 杜浩藩,丛爽.基于MATLAB 小波去噪方法的研究[J].计算机仿真, 2003, 20(7): 119-123.

[15] 飞思科技产品研发中心.MATLAB 6.5辅助小波分析与应用[M].北京:电子工业出版社, 2003.

[16] 杨书申,邵龙义,杨园园.北京、上海两地2004 和2005 年大气污染特征对比分析[J].长江流域资源与环境, 2008, 17(2): 0323-0327.

[17] 北京市环境保护局.北京市空气质量月报[EB/OL].[2013-03-10].http://www.bjepb.gov.cn/portal0/tab223 /info8206.htm.