压实方式影响路基湿度场演变规律数值试验研究

柳志军

(中国矿业大学 深部岩土力学与地下工程国家重点实验室，力学与建筑工程学院，江苏 徐州，221116)

路基工程病害问题一直是公路交通科技研究的重要课题，湿度是影响路基强度并导致病害的最显著因素之一，路基湿度场的变化将使路基工程力学性能显著改变[1]，为此，探究路基湿度场演变规律是研究和解决路基工程病害的核心问题之一[2]。降雨入渗路基是影响路基湿度场波动最常见形式[3-4]，而这种波动受公路状态差异的影响，公路状态差异的最大体现之一就是因公路等级不同而路基具备不同压实度[5]，压实度变化直接导致路基土的孔隙比产生改变进而对水迁移过程产生较大影响[6]，即作为重要因素，压实度显著影响雨水入渗路基后湿度场分布与演变。相关研究结果[7-15]表明目前这方面的研究及成果存在的主要问题是：(1) 研究主要基于一维土柱的入渗后湿度场的分布，而大多忽略了路基入渗为二维入渗分布问题；凡涉及二维入渗问题的研究目前也是仅考虑水由路基上部入渗，明显与实际工况不符；凡涉及由边坡入渗研究仅限于分析边坡表层一定厚度的湿度场分布，未深入研究路基内部主体湿度场入渗演变规律；(2) 对于路基状态来说，未考虑压实度在路堤各压实区的组合变化，未反映出路基真实的压实度状态。因此，本文作者基于降雨二维入渗扰动路基湿度场方式，紧密贴合工程实际工况，研究不同压实度以及压实区组合条件下的路基湿度场演变规律，为路基设计和病害防治工作提供理论参考。

1 试验方案设计

采用专业土体有限元渗流数值分析软件SEEP/W对降雨入渗路基湿度场演变过程进行模拟试验分析。鉴于公路横断面整体在几何尺寸上为中心轴对称，因此取半幅进行研究。路基顶宽为13 m，路基高度为3 m，地基厚度为15 m，路基初始体积含水率为15.9%，地下水位为7 m，边坡坡率为1:1.5。数值模型网格划分7 434 个单元、7 592 个节点。边界条件为：路面、路肩以及中间带不透水(表层设置为空材料)，入渗面为边坡以及边坡外地基，降雨强度为144 mm/d，降雨历时4 d，见图1。

图1 路基湿度场数值模型Fig.1 Numerical model of subgrade humidity field

从研究压实度影响路基湿度场演变规律的需要角度，数值模拟试验的路基按照取不同压实度以及压实度组合方式分为4 个试验模型，见表1。读测路基湿度的位置分别为距离路槽底下30，120 和250 cm 水平层位(分别代表路床区、上路堤区和下路堤区)。

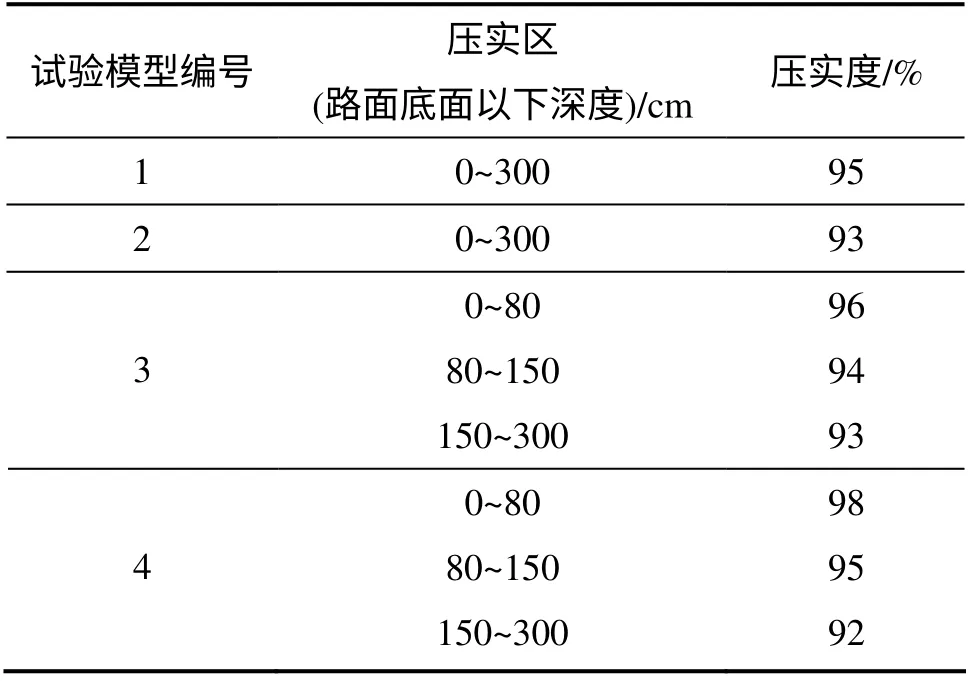
表1 试验模型初始压实度Table 1 Initial compaction degrees of test models

2 试验测试与结果分析

2.1 土质物理性质

试验测定土样的液限为35.9%，塑限为21.0%，塑性指数(IP)为14.9，最佳含水率(质量分数)为11.6%，最大干密度为1.87 g/cm3。筛分颗粒分析见表2。

表2 土样颗粒分析Table 2 Soil grain size analysis

2.2 水分运动参数试验测试

基于Van Genuchten 模型，参照文献[16]确定不同压实度K 情况下水分特征曲线见图2。

2.3 路基湿度场演变规律分析

施加降雨历时4 d 后，各压实度情况下的路基湿度场变化云图见图3。

由图3 可知：降雨入渗引起了路基湿度场发生改变，雨水自边坡渗入路基内部湿度场，湿度等值线向路基内部呈现弧形扩散形成了湿度扰动区，即由降雨入渗引起的边坡至湿润峰之间湿度异于初始湿度的区域。根据图3 数值试验结果，绘制不同压实度条件下路基30 cm 层位的湿度分布见图4。

图2 水分特征曲线Fig.2 Soil water characteristic curves

由图4 可知：自坡表水平向路基内侧，在扰动区中湿度状态由饱和过渡到非饱和并终降至初始湿度。而延着扰动区扩展的前进方向，整个湿度扰动区又可划分为前、后2 个区域：后区为靠近边坡一侧，其表现为湿度较大、梯度较小(与路基坡表湿度相差10%之内)；前区为靠近湿度前锋一侧，其表现为湿度较小、梯度较大。降雨历时相同，受到路基压实度的影响，前区和后区的范围差异较明显，其基本规律为：湿度扰动区范围和湿度随压实度增大而减小，前扰动区的曲线变陡，湿度梯度不断增大。为此，针对路基30 cm层位，分别绘制的扰动区扩距、距边坡不同位置的湿度以及前扰动区湿度梯度随压实度变化规律见图5～7。

由图5 和图6 可知：扰动区扩距和湿度2 个特征量都随着路床压实度的增加而逐渐降低，这表明压实度增大路基土空隙率减小，结构致密使得水分入渗迁移越发困难。基本变化规律符合Dw=aK+b 线性递减，其中Dw为特征量；K 为路基土压实度；参数a 和b计算时受降雨强度、历时和路基初始湿度3 个因素的主要影响。另外，在计算湿度时还需考虑点位因素影响，计算点位愈靠近边坡则线性关系愈明显。由图7可知： 前扰动区湿度梯度随着压实度呈G=0.03K-2.46(R2=0.98)线性递增，其中G 为前扰动区湿度梯度，m2/m3；K 为路基土压实度，%。

图3 压实度影响路基湿度场云图Fig.3 Contours of subgrade humidity field affected by compaction degree

图4 30 cm 层位湿度分布Fig.4 Humidity distributions at 30 cm horizon

图5 扰动区扩距与压实度关系Fig.5 Relationship between extended distance in disturbed zone and compaction degree

图6 路基湿度与压实度关系Fig.6 Relationship between subgrade humidity and compaction degree

图7 前扰动区湿度梯度与压实度关系Fig.7 Relationship between humidity gradient in front disturbed zone and compaction degree

湿度场云图(图3)中各图对比显示：图3(a)和3(b)所示的单一压实区状况显示扰动区湿度形态比较均一，而当路基压实度进行分区后，图3(c)和3(d)所示的湿度场形态明显呈现阶梯状变化。为此，绘制120 cm 和250 cm 层位的路基湿度分布状态见图8。

图8 路基不同层位湿度分布Fig.8 Humidity distributions at different subgrade horizons

由图8 可知：具有压实区组合状态的路基湿度场根据组合方式不同其变化有所差异。主要表现为：对于边坡表层来说，因其在强降雨下迅速达到饱和状态，因此，无论压实区采用何种组合方式，湿度变化规律与单一压实区的情况相同，即压实度相同处湿度相等；受到上部压实区不同压实度的影响，下部压实区湿度场分布曲线出现了交叉现象，如图8(a)所示，受到路床96%压实度的影响，模型3 曲线上路堤湿度随着向路基内部延伸下降速度比模型1 曲线的快，2 条曲线出现了交叉；同样图8(b)表明：模型4 曲线的下路堤坡表湿度最大，随着向路基内部延伸，其湿度降速明显比其他3 个曲线的快，其原因也是因为模型4 的路床和上路堤压实度比其他3 个模型的大，这些都充分表明下部压实区湿度受上部压实区压实度影响显著。

为了获得这种影响规律，基于模型4 开展试验，保持整个路堤区压实度为92%，而将路床区压实度分别取92%，94%，96%和98% 4 种，经过降雨试验后读取120 cm 层位、距离边坡11 m 处(非饱和扰动区)湿度受不同路床压实度影响下的曲线见图9。

图9 路堤湿度与路床压实度关系Fig.9 Relationship between embankment humidity and roadbed compaction degree

由图9 可知：受路床压实度影响，路堤湿度呈w=-0.009K+1.051(R2=0.96)线性递减，其中w 为路堤湿度，m3/m3；K 为路床压实度，%；此现象表明：雨水入渗路基速度矢量的竖向分量远大于水平向分量，当上层压实度较大时，水分向下迁移困难，造成下层湿度增量减小，因此下层路基湿度变化受上层路基压实度影响显著。

3 结论

(1) 降雨入渗路基产生湿度扰动区按照扩展的方向可划分为前、后2 个区域，后区为靠近边坡一侧，其表现为湿度较大、梯度较小(与路基坡表湿度相差10%之内)；前区为靠近湿度前锋一侧，其表现为湿度较小、梯度较大。

(2) 由于压实度增大后路基土体空隙率减小，结构致密使得水分入渗迁移越发困难，因此，湿度扰动区扩距随着路基压实度的增加而呈线性减小；湿度随着路基压实度的增加而呈线性降低，且湿度测点位置愈靠近边坡这种线性关系愈发明显；前扰动区的湿度梯度随着路基压实度呈线性递增。

(3) 在相同的降雨入渗条件下，受到路基压实区组合方式影响，非饱和扰动区的下层路基湿度随上层路基压实度增加呈线性降低，表明雨水入渗路基速度矢量的竖向分量远大于水平向分量，当上层压实度较大时，水分向下迁移困难，造成下层湿度增量减小，下层路基湿度变化受上层路基压实度影响显著。

[1] 李同祥. 基于土力学剪应力理论的沥青路面开裂分析[J]. 公路交通科技, 2005, 22(7): 14-18.LI Tongxiang. Analysis of bituminous pavement crackings based on soil mechanics shear stress theory[J]. Journal of Highway and Transportation Research and Development, 2005, 22(7): 14-18.

[2] Tarefder R A, Saha N, Stormont J C. Evaluation of subgrade strength and pavement designs for reliability [J]. Journal of Transportation Engineering, 2010, 136(4): 379-391.

[3] Gang Z, Wright W C, Rainwater N R, et al. Factors affecting determination of subgrade water content from multisegment time domain reflectometry probes[J]. Transportation Research Record,2002, 1808: 3-10.

[4] Heydinger A G, Davies B O A. Analysis of variations of pavement subgrade soil water content[J]. Geotechnical Special Publication, 2006, 147: 247-257.

[5] JTG D30—2004. 公路路基设计规范[S].JTG D30—2004. Pecifications for design of highway subg rades[S].

[6] Assouline S. A model for soil relative hydraulic conductivity based on the waterretention characteristic curve[J]. Water Reources Research, 2001, 37(2): 265-271.

[7] 王铁行, 岳彩坤, 鲁洁, 等. 连续降雨条件下黄土路基水分场数值分析[J]. 西安建筑科技大学学报(自然科学版), 2007,39(5): 593-597.WANG Tiehang, YUE Caikun, LU Jie, et al. Numerical analysis on moisture migration in loess subgrade under rainfall[J].Journal of Xi’an University of Architecture & Technology(Natural Science Edition), 2007, 39(5): 593-597.

[8] Kim Y K, Lee S R. Field infiltration characteristics of natural rainfall in compacted roadside slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(1): 248-252.

[9] Xue J, Gavin K. Effect of rainfall intensity on infiltration into partly saturated slopes[J]. Geotechnical and Geological Engineering, 2008, 26(2): 199-209.

[10] Schmertmann J H, Gavin K. Estimating slope stability reduction due to rain infiltration mounding[J]. Geotechnical and Geological Engineering, 2006, 132(9): 1219-1228.

[11] 程海涛, 刘保健, 柳学花. 黄土地基积水入渗规律研究[J]. 中外公路, 2008, 28(6): 29-31.CHENG Haitao, LIU Baojian, LIU Xuehua. Study on the moisture infiltration law of loess subgrade[J]. Journal of China &Foreign Highway, 2008, 28(6): 29-31.

[12] Kim J, Jeong S, Park S, et al. Influence of rainfall-induced wetting on the stability of slopes in weathered soils[J].Engineering Geology, 2004, 75(4): 251-262.

[13] Phan T H, Cushman M D, White D J. Seasonal variation in the subgrade and base layers of U.S. highway 20,Iowa[C]//Proceedings of the 2007 Mid-Continent Transportation Research Symposium. Iowa: Iowa Department of Transportation,2007: 1-13.

[14] 景宏君. 黄土路基积水入渗规律研究[J]. 公路交通科技, 2004,21(4): 40-42.JING Hongjun. Study on water infiltration pattern into loess subgrade[J]. Journal of Highway and Transportation Research and Development, 2004, 21(4): 40-42.

[15] 刘巍然, 高江平. 压实黄土路基中含水量的分布及水分迁移规律研究[J]. 长安大学学报(自然科学版), 2006, 26(4): 5-7.LIU Weiran, GAO Jiangping. Numerical modelling on water migration in loess subgrade[J]. Journal of Changan University(Natural Science Edition), 2006, 26(4): 5-7.

[16] 柳志军. 西部干旱半干旱地区公路路基湿度场演变规律研究[D]. 徐州: 中国矿业大学力学与建筑工程学院, 2012: 1-120.LIU Zhijun. The evolution of highway subgrade humidity field in western arid and semi arid regions[D]. Xuzhou: China University of Mining & Technology. School of Mechanics &Civil Engineering, 2012: 1-120.