露天矿排土场滑坡的可拓评价预警

栾婷婷，谢振华，吴宗之，张雪冬

(1. 北京科技大学 土木与环境工程学院，北京，100083；2. 中国安全生产科学研究院，北京，100029)

排土场的灾害形式因地质、地理、气候等自然条件不同而异，按照其对环境危害的表现形式，大体上可分以下三大类：排土场滑坡、排土场泥石流和排土场环境污染[1]。其中，排土场滑坡是发生最普遍、频率最高的一种排土场灾害现象，其受到内外多种因素的共同影响，表现出很大的动态性和复杂性。基于这种动态性和复杂性，在边坡稳定性分析中多采用非确定性方法。可拓理论中的参变量物元模型是动态模型，能很好地拟合像滑坡这样复杂的、动态变化的系统。王新民等[2]综合运用物元概念的可拓学理论与层次分析法，建立多层次多指标的岩质边坡稳定性综合评价模型，对边坡稳定性进行评价，得出安全等级标准及评价指标量值。王润生等[3]基于物元模型的可拓学理论分析，提出了高陡边坡岩体稳定性的可拓学预测方法；李克钢等[4]以某实际边坡工程为例，建立边坡稳定性评价的可拓模型，将预测结果与传统的模糊评判结果进行对比，证明了该方法可行性。运用可拓理论进行评价时，多以层次分析法来确定指标权重，然而，将可拓理论与未确知有理数确定权重法结合可以使权重的计算更加客观、准确，提高预警的效率和精度。

1 预警指标体系的建立

露天矿排土场边坡稳定性的影响因素是比较复杂的，本课题组对国内一些典型露天矿排土场进行了实地考察研究，结合文献[5-8]并搜集整理了国内外近50年来排土场典型灾害的事故案例，从滑坡事故发生的原因考虑，排土场滑坡的影响因素主要可以从内因和外因2 方面进行分析，初步确定从排土场物料的力学性质、地基影响、边坡高度、降雨影响、安全监测等5 个大的方面来考虑影响排土场滑坡的因素。这些因素下面又包含许多具体的评价指标，当然，这些指标对滑坡的影响有轻重主次之分。为了使模型的计算可以简便、高效，权衡各指标的获取和量化的难易程度，在征求该领域相关专家意见之后，最终选取黏聚力、内摩擦角、地基坡度、边坡高度、最大日雨量和地表裂缝6 个评价指标。建立的露天矿排土场滑坡预警指标体系如图1 所示。

为了构建排土场滑坡的可拓评价预警模型，将建立的预警指标的取值范围与预警等级进行一一对应，参考我国突发事件的预警级别及排土场边坡稳定性状态分类[9]，将排土场的滑坡预警模式按照灾害的紧急程度、发展势态和可能造成的危害程度划分为5 个等级：无警、蓝色预警、黄色预警、橙色预警和红色预警，分别记为：N1，N2，N3，N4和N5，对应的滑坡危险性从小到大。预警指标的取值范围与预警等级的对应关系参考了现有的岩土边坡的研究成果和文献[2-3,10-11]，并咨询了有关专家的意见，建立了排土场滑坡评价预警指标的数据取值的划分标准，预警指标与预警等级的对照表如表1 所示。

图1 露天矿排土场滑坡预警指标体系Fig.1 Early-warning index system of waste dump landslide in open-pit mine

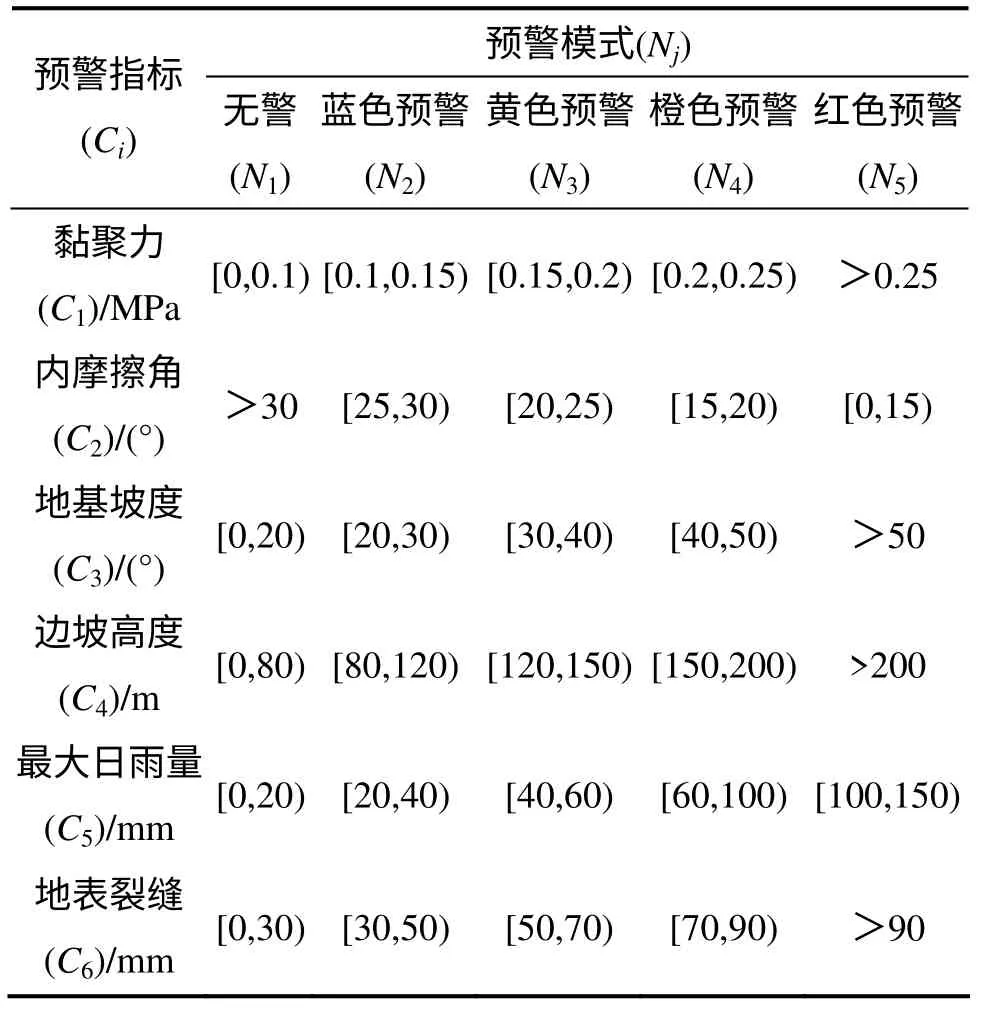
表1 排土场滑坡预警指标与预警等级对应表Table 1 Mapping table between early-warning indicators and rank of waste dump landslide

2 可拓评价预警模型

近年来，利用可拓理论进行的评价预警研究在很多领域得到了广泛应用[12-14]，可拓评价是在物元模型和可拓集合理论基础上建立起来的一种评价方法，它是定性分析与定量计算的结合，通过物元的可拓性进行定性分析，再利用可拓集合理论中的关联函数进行定量计算。本文在可拓理论的基础上，建立了排土场滑坡的评价预警模型，如图2 所示。

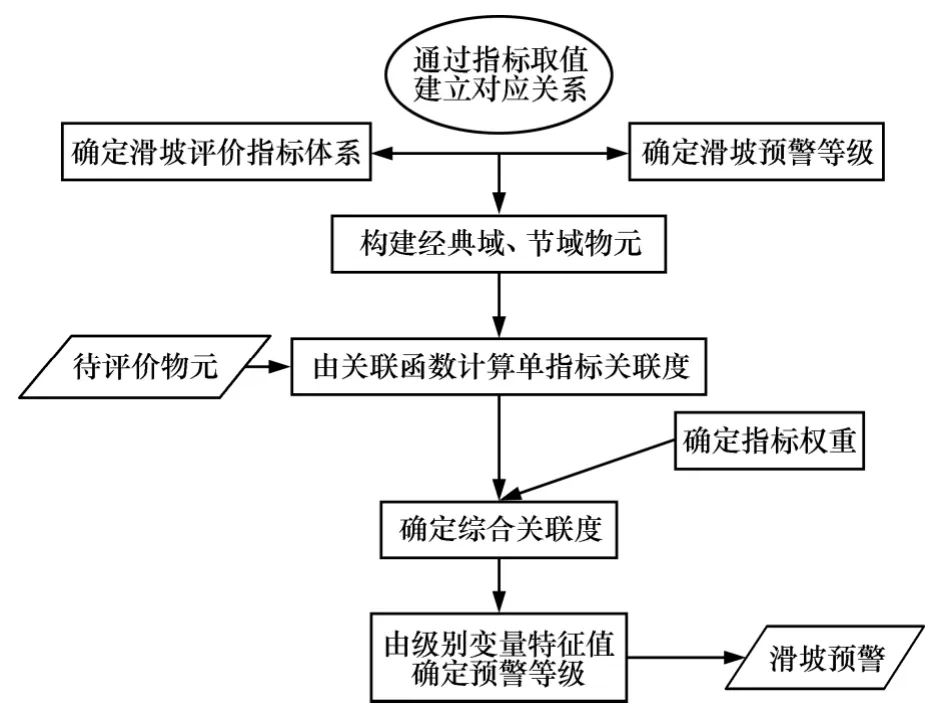
图2 排土场滑坡的可拓评价预警模型Fig.2 Extension evaluation and warning model of waste dump landslide

物元是可拓学的逻辑细胞，以有序三元组R=(N，C，V)表示(其中，N 表示事物，C 表示特征，V 表示N关于C 所取的量值)。可拓评价预警模型的具体步骤如下所示[15-16]。

2.1 确定经典域、节域和待评价物元

(1) 经典域物元：

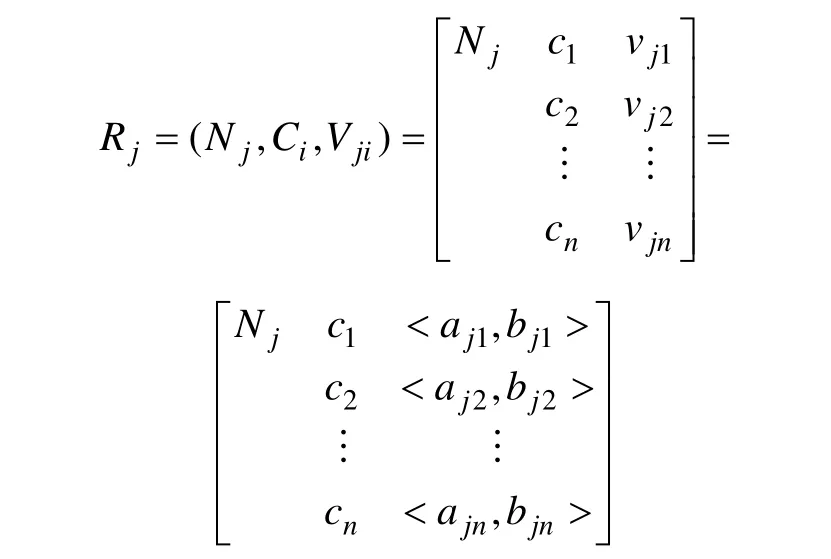
其中：Nj表示所划分的第j 个评价等级；Ci表示第i个评价指标，Vji表示等级Nj关于Ci的取值范围，即经典域，Vji=＜aji,bji＞，其中i 为评价指标数i=(1，2，…，n)；j 为评价等级数j=(1，2，…，m)。

(2) 节域物元：

其中：N 表示全部评价等级，Vpi为Ci在等级N 下的所有取值范围，物元模型中各评价指标Ci对应所有状态Nj的量值范围Vpi=＜api,bpi＞即节域。显然，有＜aji,bji＞⊂＜api,bpi＞。

(3) 待评价物元：

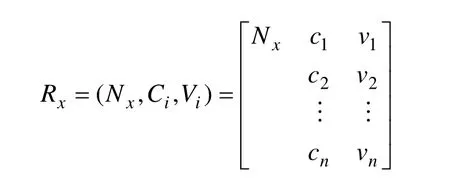
其中：Nx表示待评价事物；Vi为Nx关于指标Ci的具体数据。

2.2 确定各预警指标关于各预警等级的关联度

(1) 计算各单项预警指标关于各预警等级的关联度Kj(vi)如下：

其中：ρ(vi,vji)为点vi与区间Vji的距，

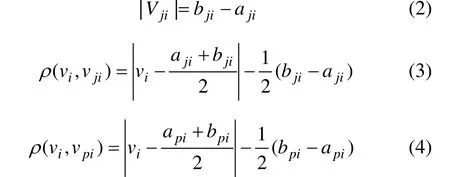
(2) 计算待评价物元关于预警等级Nj的综合关联度

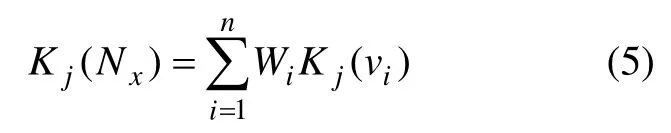
2.3 预警等级评定

若Kj=maxj∈(1,2,…,m)kj(Nx)则预警对象Nx的预警等级为j。若

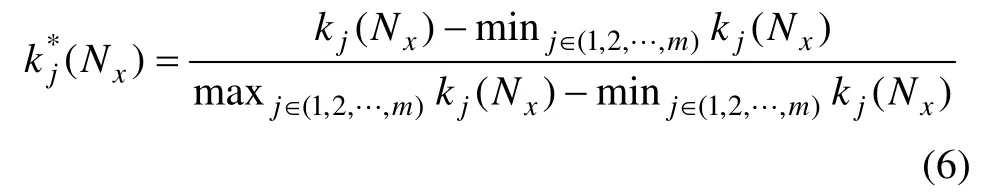
则

j*为事物Nx的级别变量特征值。

3 未确知有理数法确定指标权重

评价指标的重要性不尽相同，通常采用权重来反映重要性的差别。权重确定的合理性直接影响整个评价模型的计算结果，通常应用的层次分析法在评价指标比较多时，易产生模糊判断， 使不确定性增加，并且给出的判断矩阵很难满足一致性要求的问题。廖瑞金等[17]提出了一种未确知有理数的权重确定方法，计算简便，结果更加精确，在实际应用中取得了很好的效果，因此，本文在可拓评价预警模型的基础上引入未确知有理数法计算评价指标的权重值。

3.1 未确知有理数的概念

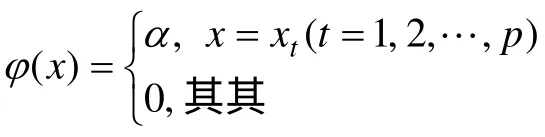
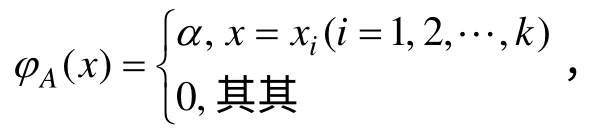
3.2 权重计算的步骤

未确知有理数确定指标权重的步骤归纳如下[18]。

选择10 位专家对评价指标的重要性进行评价，专家在1～10 之间给出指标重要性取值区间及对应值下的信度分布，指标对排土场滑坡的影响越大，重要性评价值就越大，百分数由专家根据经验给出，表示指标重要性在取值区间对应值下的信度分布。最终选取5 位可信度高的专家意见作为处理对象。

构造评价指标的重要性未确知有理数A=[[1,10],φA(x)]，求得该指标的可信度分布密度函数φA(x)。

根据评价指标的可信度分布密度函数φA(x)，计算指标未确知有理数的数学期望值E(A)=[[x,x],φA′(x)]。

由未确知有理数的概念可知E(A)是一阶未确知有理数，x 仅在一点处可信度不为0，那么，这个不为0的点即评价指标的权重。

3.3 权重计算的结果

本文以黏聚力指标为例说明预警指标权重的计算过程，我们根据专家的信息，应用文献[16]中的专家权威性量化标准，选取权重较高的5 位专家评判结果作为处理对象，5 位专家的权重值分别为：0.9，0.81，0.75，0.75，0.69；归一化得：0.23，0.21，0.19，0.19，0.18。表2 所示为黏聚力指标的重要性评价值及信度分布。

表2 黏聚力的重要性评价值及信度分布Table 2 Survey results of cohesive force %

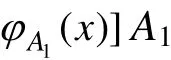
可求得黏聚力重要性程度未确知有理数的数学期望值：

数学期望仅在x=4.788 时不为0，因此，黏聚力指标的权重值为4.788，同理可以得到其其预警指标的权重值分别为：内摩擦角4.626；地基坡度5.404；边坡高度的权重为5.333，最大日雨量5.742；地表裂缝6.271；归一化得到W=(0.149，0.143，0.168，0.166，0.179，0.195)。

4 实例应用

选取我国中部地区某典型露天铁矿排土场作为工程实例，排土场位于露天采场的南部，地基为黄土软弱地基，分为2 个台阶，土场分段高度80～100 m，最终堆高达200～300 m。该排土场的边坡高度为45 m，边坡角为36°。该地区属大陆性半干旱高原季风气候，最高气温36 ℃，最低气温-21.4 ℃，年降雨量为440～600 mm，降水主要集中在7～8 月份。

4.1 构建可拓物元模型

依据前面的可拓理论，构造排土场滑坡预警评价的经典域为R1，R2，R3，R4，R5。

节域为Rp；待评价物元为Rx。

4.2 计算待评价物元的关联度

根据已经建立的排土场滑坡可拓评价预警模型和上面确定的经典域、节域、待评价物元，由式(1)至(4)计算出待评价物元中各指标关于滑坡预警等级的关联函数值，如表3 所示。

表3 滑坡预警等级的关联函数值Table 3 Correlation function values of landslide early-warning rank

由式(5)计算待评价物元的综合关联度为：K1(Nx)=-0.080 6；K2(Nx)=-0.032 66；K3(Nx)=-0.160 7；K4(Nx)=-0.444；K5(Nx)=-0.586 35。

4.3 确定预警等级

K2(Nx)=maxKj(Nx)，则该排土场的滑坡预警等级为蓝色预警。由式(6)和(7)得到：K1*(Nx)=0.913 4；K2*(Nx)=1.000 0；K3*(Nx)=0.768 8；K4*(Nx)=0.257 1；K5*(Nx)=0。

则级别变量特征值为

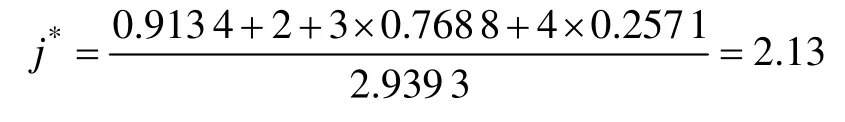
由级别变量特征值可以看出：此次评价的预警等级在蓝色预警和黄色预警之间，主要偏向于蓝色预警等级，说明此时排土场存在发生滑坡的风险，但是风险不大，矿山企业根据上述判断可以采取相应的应急预案和安全防护措施。

5 结论

(1) 排土场滑坡受多种因素制约，对于滑坡预警指标的选取也不能局限于单一的某个因素，而应考虑多因素共同作用的结果，可拓理论正好符合这种多因素的要求，从定性与定量两方面对滑坡预警的等级进行评价，为排土场的滑坡预警提供了一种新方法。

(2) 针对于可拓理论中指标权重确定的问题，提出了一种新的权重确定方法，即采用未确知数学的原理，构造预警指标的重要性未确知有理数，通过求得其数学期望值，进而求得该指标的权重值，该方法具有很好的数学依据，避免了结果过多受人为主观影响的现象，使权值的计算更加准确，提高了预警模型的精度。

(3) 以典型的某露天矿山排土场为工程实例，进行实际应用，应用结果与排土场的实际情况相吻合，较好地说明了该方法是科学、有效的；通过计算预警等级的级别变量特征值，使矿山企业更加准确的掌握排土场的滑坡风险，是预防滑坡灾害发生、确保矿山安全生产的重要途径。

[1] 龙虎荣. 露天矿山排土场灾害分析与防治措施[J]. 矿冶工程,010, 30(1): 21-22.LONG Hurong. Disaster assessment and prevention measures for the waste dump of open-pit mine[J]. Mining and Metallurg Ical Eng Ineering, 2010, 30(1): 21-22.

[2] 王新民, 康虔, 秦健春, 等. 层次分析法-可拓学模型在岩质边坡稳定性安全评价中的应用[J]. 中南大学学报(自然科学版), 2013, 44(16): 2455-2462.WANG Xinmin, KANG Qian, QIN Jianchun, et al. Application of AHP-extenics model to safety evaluation of rock slope stability[J]. Journal of Central South University (Science and Technology), 2013, 44(16): 2455-2462.

[3] 王润生, 李存国, 郭立稳. 基于可拓理论的高陡边坡稳定性评价[J].矿业安全与环保, 2008, 35(6): 25-28.WANG Runsheng, LI Cunguo, GUO Liwen. Stability evaluation for high and steep slope based on the extension theory[J].Mining Safetyvand Environmental Protection, 2008, 35(6):25-28.

[4] 李克钢, 许江, 李树春, 等. 基于可拓理论的边坡稳定性评价研究[J]. 重庆建筑大学学报, 2007, 29(4): 76-78.LI Kegang, XU Jing, LI Shuchun, et al. Research on evaluation of the slope stability based on the extension theory[J]. Journal of Chongqing Jianzhu University, 2007, 29(4): 76-78.

[5] 杨胜利, 王云鹏. 排土场稳定性影响因素分析[J]. 露天采矿技术, 2010(3): 4-7.YANG Shengli, WANG Yunpeng. Analysis of factors affecting dump stability[J]. Opencast Mining Technology, 2010(3): 4-7.

[6] 马福恒, 何心望, 吴光耀. 土石坝风险预警指标体系研究[J].岩土工程学报, 2008, 30(11): 1735-1737.MA Fuheng, HE Xinwang, WU Guangyao. Risk early-warning index system for earth and rockfill dams[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(11): 1735-1737.

[7] 谢旭阳, 王云海, 张兴凯. 尾矿库区域预警指标体系的建立[J]. 中国安全科学学报, 2008, 18(5): 167-171.XIE Xuyang, WANG Yunhai, ZHANG Xingkai. Establishment of regional pre-warning index system for tailing reservoirs[J].China Safety Science Journal, 2008, 18(5): 167-171.

[8] 王运敏, 项宏海. 排土场稳定性及灾害防治[M]. 北京: 冶金工业出版社, 2011: 50-61.WANG Yunming, XIANG Honghai. Stability of dump and its disaster prevention and control[M]. Beijing: Metallurgical Industry Press, 2011: 50-61.

[9] 缪旭明, 李泽椿, 田浩. 关于突发事件预警级别划分标准及对策的研究[J]. 中国应急管理, 2011(5): 33-36.MIAO Xuming, LI Zechun, TIAN Hao. Research on emergency alert level division standard and countermeasure[J]. China Emergency Management, 2011(5): 33-36.

[10] 王东耀, 折学森, 叶万军. 基于可拓工程法的黄土路堑边坡稳定性评价方法[J]. 地球科学与环境学报, 2006, 28(3): 57-60.WANG Dongyao, SHE Xuesen, YE Wanjun. Method for stability of loess slope of cut based on topology[J]. Journal of Earth Sciences and Environment, 2006, 28(3): 57-60.

[11] 金海元. 岩石高边坡监测预警综合评价方法研究[J]. 长江科学院院报, 2011, 28(1): 29-33.JIN Haiyuan. Research on comprehensive evaluation methods of monitoring and early-warning for rock slope[J]. Journal of Yangtze River Scientific Research Institute, 2011, 28(1): 29-33.

[12] 王进, 喻珍. 城市轨道交通次生环境影响可拓综合评价[J].中南大学学报(自然科学版), 2007, 38(5): 1007-1011.WANG Jin, YU Zhen. Comprehensive extension evaluation of secondary environment impacts of urban rail transit[J]. Journal of Central South University (Science and Technology), 2007,38(5):1007-1011.

[13] 姚韵, 朱金福. 基于可拓关联函数的不正常航班管理预警模型[J]. 西南交通大学学报, 2008, 42(1): 102-106.YAO Yun, ZHU Jinfu. Early-warning model of irregular flight management based on correlation function in extension theory[J].Journal of Southwest Jiaotong University, 2008, 42(1): 102-106.

[14] 杨玉中, 冯长根, 吴立云. 基于可拓理论的煤矿安全预警模型研究[J]. 中国安全科学学报, 2008, 18(1): 42-44.YANG Yuzhong, FENG Changgen, WU Liyun. Research on early-warning model for coal mine safety based on extension theory[J]. China Safety Science Journal, 2008, 18(1): 42-44.

[15] 宋金玲, 刘国华, 王丹丽, 等. 基于可拓方法的职业危害控制水平预警模型[J]. 中国安全生产科学技术, 2009, 5(1):112-116.SONG Jinling, LIU Guohua, WANG Danli, et al. Early warning model for control level of occupational hazards based on extension method[J]. Journal of Safety Science and Technology,2009, 5(1): 112-116.

[16] 刘爱华, 程力, 董陇军. 可拓学理论在东戈壁露天矿工程岩体质量评价中的应用[J]. 中南大学学报(自然科学版), 2013,44(7): 2843-2847.LIU Aihua, CHENG Li, DONG Longjun. Evaluation of engineering rock mass quality based on theory of extenics in Dong Gebi open-pit mine[J]. Journal of Central South University(Science and Technology), 2013, 44(7): 2843-2847.

[17] 廖瑞金, 黄飞龙, 杨丽君, 等. 变压器状态评估指标权重计算的未确知有理数法[J]. 高电压技术, 2010, 36(9): 2219-2224.LIAO Ruijin, HUANG Feilong, YANG Lijun, et al. Calculation method of power transformer condition assessment index weight using unascertained theory[J]. High Voltage Engineering, 2010,36(9): 2219-2224.

[18] 王光远. 未确知信息及其数学处理[J]. 哈尔滨建筑工程学院学报, 1990, 23(4): 1-9.WANG Guangyuan. Uncertainty information and its mathematical treatment[J]. Journal of Harbin Architecture and Engineering Institute, 1990, 23(4): 1-9.

[19] 刘开第, 吴和琴. 不确定性信息数学处理及应用[M]. 北京:科学出版社, 1999.LIU Kaidi, WU Heqin. Uncertain information mathematical processing and application[M]. Beijing: Science Press, 1999.