混流式喷水推进泵叶轮强度计算和分析

李留洋，王永生，魏应三，付建，靳栓宝

(海军工程大学 动力工程学院，湖北 武汉，430033)

喷水推进以其机动性好、操纵性优、高航速推进效率高、振动噪声小、抗空化能力强等特点在各国海军舰艇和民用船舶上得到了广泛应用。叶轮作为其核心部件承载着高转速、大推力、强载荷，是整个喷水推进器最主要的部件，其结构强度直接关系到喷水推进器的安全性和可靠性, 对于喷水推进装置的安全运行至关重要，因此，进行叶轮强度的计算是非常必要的。国内外已有很多学者和研究人员对旋转机械如水轮机、压气机、水泵的强度进行了分析，但有关喷水推进泵(简称喷泵)叶轮强度的研究在国内并不多见。郑小波等[1]利用双向流固耦合的方法计算了轴流式水轮机叶片的强度；吴刚等[2]结合经验公式推出了等环量和变环量设计下的强度校核公式；董新国[3]利用经验公式和流固耦合的方法计算了喷泵的动叶轮和导叶的静强度；Katsutoshi 等[4-5]利用计算流体力学(CFD)方法模拟了流场宏观特性并结合单向流固耦合方法计算了不同流量下混流泵的叶片应力分布，并指出当流量偏离设计值70%时叶片表面压力达到最大值。Lerche 等[6]利用流固耦合方法计算了轴流式压气机叶片在时域上的动应力，并与实验结果进行了对比，验证了所用方法的准确性。Benra[7]以单叶轮污水泵为研究对象，利用流固耦合计算了叶片的变形并和实验结果进行对比，二者吻合良好。从上述文献可知单向流固耦合方法计算叶片应力和变形的有效性和准确性已在工程界得到认可，但是文献中只是计算了其中的静强度或者动强度。本文作者利用单向流固耦合的方法以某国外混流式喷泵为对象，通过CFD 计算出喷泵的水动力性能的空间分布载荷，结合有限元(FEM)方法同时计算和分析喷泵叶轮的静强度和动强度，并对2种强度特性进行比较。

1 CFD 模拟计算

1.1 控制方程和湍流模型

设喷水推进器内流动为定常不可压缩流动，连续方程和动量方程为

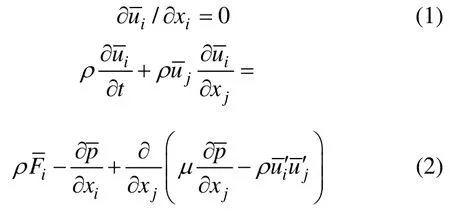
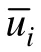
本文作者采用SST 剪切应力模型来封闭方程组，集合了k-ε 模型和k-ω 模型的优点：近壁面区域采用k-ω 模型模拟，湍流耗散较小，收敛性好；在湍流充分发展区域，采用k-ε，计算效率高，对复杂流场的适应性较好。SST 把2 种模型结合成能够较好地模拟黏性底层的流动。

1.2 敞水喷泵性能计算和结果验证

敞水喷泵性能是指单独的喷泵在均匀流场中所表现出来的水力性能,它是船后喷泵性能分析的基础。该喷泵叶轮叶片数为6 片，导叶为11 片，叶轮进口直径为710 mm，出口直径为446 mm。计算域采用分块六面体结构化网格进行离散，叶轮和导叶体分别采用H型和J 型拓扑结构，叶片周围嵌入O 型网格进行加密，叶顶间隙0.5 mm 采用数层H 型网格，如图1 所示。

图1 敞水泵的几何和网格划分Fig.1 Geometry and mesh of waterjet pump

在网格数量的选择上，对叶轮在880 r/min 下的流量性能参数进行了网格无关性验证，发现在网格数量大于80 万个的时候流量参数基本上不再发生变化，如图2 所示。本文权衡了计算速度和对流场流动细节的有效捕捉两方面，具体网格数和节点数见表1。对敞水喷泵进行水力性能进行计算时，为保证均匀进流，在叶轮进口前加进流直管段，长度为叶轮进口直径的2 倍。CFD 计算时采用流量进口，静压出口边界条件，叶轮叶片和轮毂设为相对静止壁面条件，泵壳设为绝对静止壁面条件。

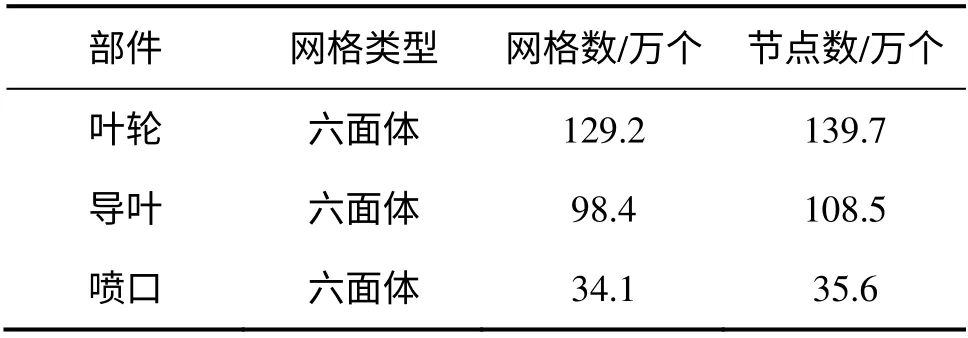
表1 各部件的网格数据Table 1 Mesh numbers of parts of waterjet

本文模拟了计算喷泵在转速880 r/min 下，流量从2.60～5.40 t/s 的扬程、功率和效率。图3 所示为喷泵的敞水性能曲线。从图3 可见：扬程和功率的规律性较为正常，在流量4.80 t/s 附近该喷泵效率最高，约88%。

图4 所示为利用CFD 方法计算出的喷泵的转速-功率曲线与厂家提供的转速-功率曲线对比。由图4可见：计算功率曲线与厂商提供的功率曲线趋势一致，计算功率与厂商提供值相对误差都在1%以内，且计算功率都小于厂商值，这是因为数值计算时没有考虑喷泵轮毂内支点轴承和推力轴承的摩擦损失。该结果直接验证了CFD 方法数值模拟喷泵内部流场的可信性。所以，用CFD 方法计算喷泵内的流动空间分布载荷并应用于强度计算有了可信的基础。

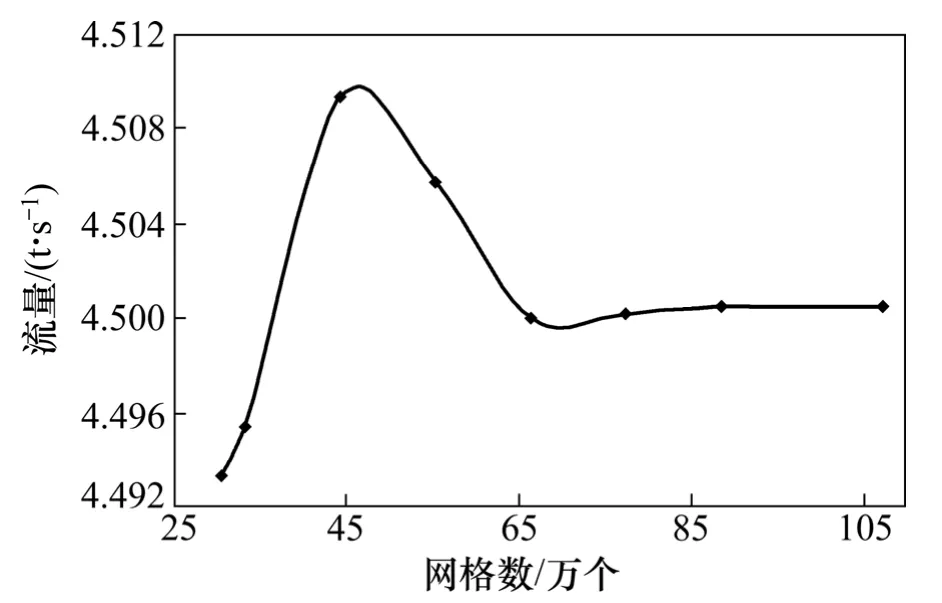
图2 叶轮网格无关性的验证Fig.2 Grid-independent validation of impeller

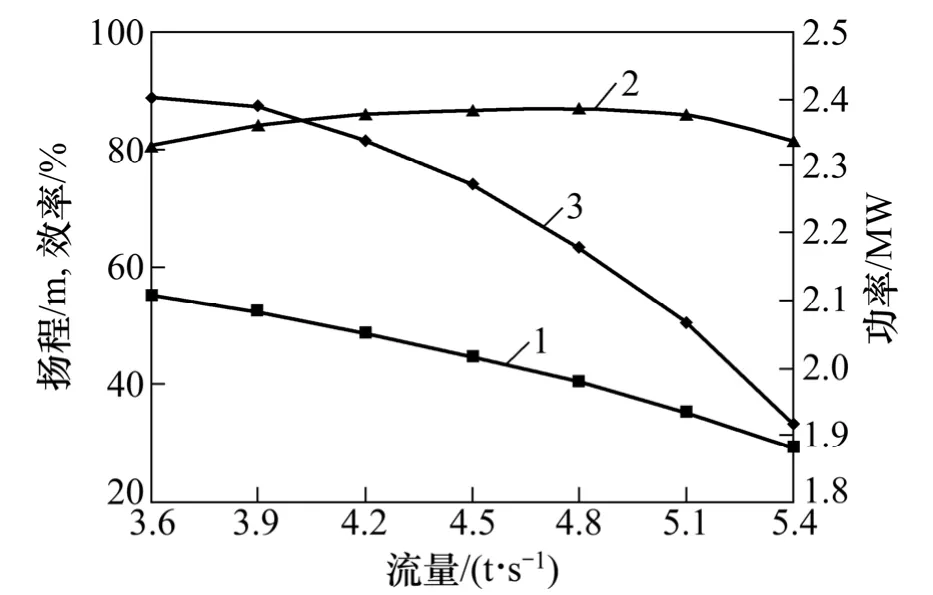
图3 喷泵的敞水性能曲线Fig.3 Performance curves of waterjet pump

图4 喷泵计算功率和厂商功率对比Fig.4 Comparison between numerical and manufacture powers

1.3 “喷泵+流道+船体”的流体动力性能计算

将“喷泵+流道+船体”组成的整体系统置于一定的控制域之中,在给定的进流或航速等边界条件下，研究喷水推进器的推进性能。受船体边界层的影响，进入进水流道的水流是不均匀的，选取计算域时将进水口外船底下方的流体也包括在内，取计算域的长、宽和深分别为喷水推进器叶轮进口直径的30 倍、10 倍和8倍[9]，如图5 所示，船底流场的两侧和靠近船头的来流面设为速度进口，喷口压力和船底出流压力设为环境压力；流道壁面、船底等设为无滑移壁面； 经网格无关性验证流道和流场控制体的网格数量均满足计算要求。

在转速880 r/min 下，不同航速下的喷水推进器的推力性能如图6 所示，各航速下对应的喷泵流量见表2。从图6 和表2 可以得到：随着航速的增加该喷泵的推力逐渐减小、效率逐渐增加和流量逐渐增加。本文计算叶轮强度的表面压力分布(即水动力载荷)是喷水推进器在转速880 r/min、航速74.8 km/h 时计算得到的。

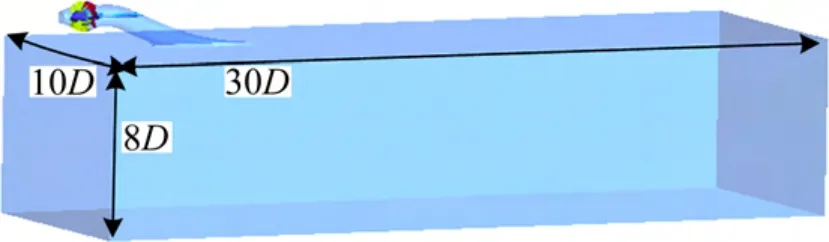
图5 “喷泵+流道+船体”模型Fig.5 System model of “waterjet pump+duct+hull”

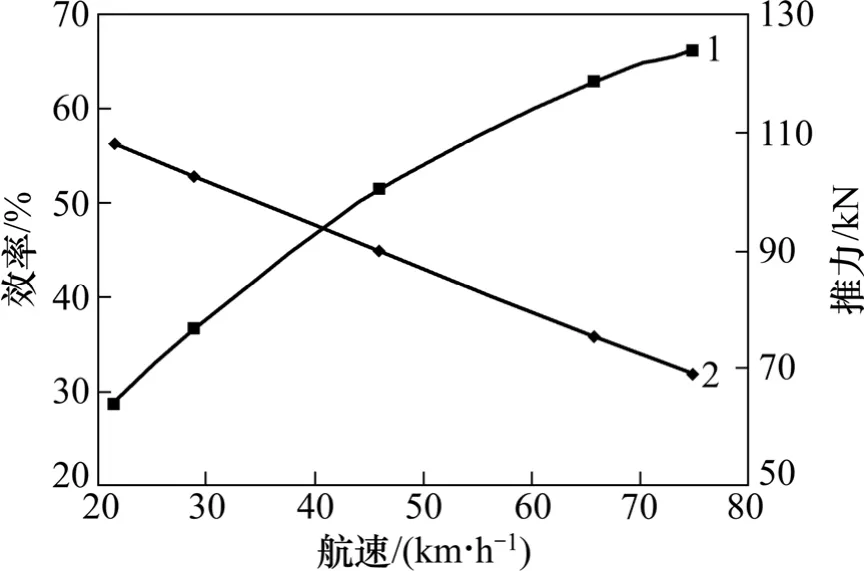
图6 喷水推进器推力性能曲线Fig.6 Thrust performance curves of waterjet propulsion

1.4 “喷泵+流道+船体”的瞬态计算

喷水推进器的非定常计算采用的是SST 模型和DES 模型结合在转速880 r/min，航速74.8 km/h 下，以稳态计算结果为初始值，以叶轮旋转1°的时间作为计算步长，叶轮旋转1 周需要计算360 步。计算总时间取为叶轮旋转周期的3 倍。瞬态计算各残差收敛良好，在叶轮进口径向0.5 倍直径处设置监测点，监测压力脉动的变化。图7 所示为叶轮进口监测点的压力脉动曲线。由图7 可见：前800 步是稳态时的监控值，800 步往后是瞬态计算的监控值；监测点的压力在1圈中有6 个峰值，变化周期性良好。

表2 喷水推进器在880 r/min 转速下各航速对应的流量Table 2 Flux at different ship speed

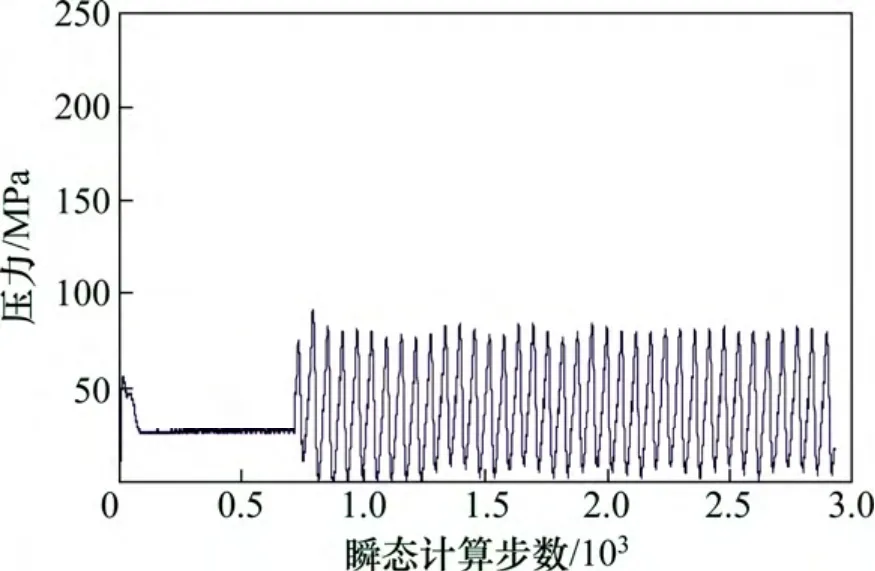
图7 叶轮进口监测点的压力脉动曲线Fig.7 Pressure fluctuation curve of monitoring points

2 叶轮强度的有限元计算

叶轮为旋转部件，建立有限元模型时省略了轮毂部分，对叶片的根部施加全约束以代替。叶片的材料为双相不锈钢，其主要材料属性如表3 所示。

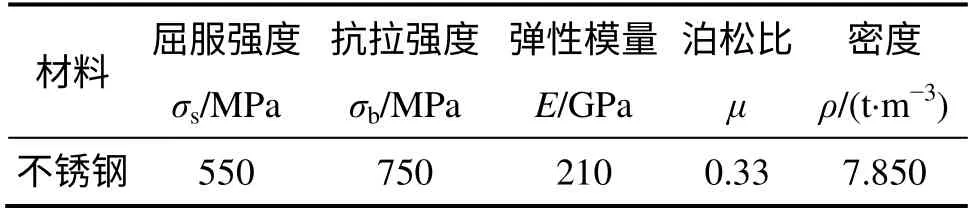
表3 叶片的材料属性Table 3 Properties of waterjet’s Blade material

生成的有限元模型如图8 所示。有限元建模时采用Solid45 八节点四面体单元对叶片进行离散。为保证计算精度及效率，叶片全部采用映射网格，并在叶片导边、随边、叶根、叶顶部位进行局部加密以捕捉应力集中现象。有限元模型有158 400 个单元，203 130个节点。

在叶片工作过程中，主要承受重力载荷、离心力载荷和水动力载荷。其中，重力载荷与叶片的自身物质属性有关，对叶片主要起压力和弯矩的作用；叶片旋转产生离心力载荷与转速有关，主要对叶片起径向的拉伸作用，取转速最大值进行计算；叶片水动力载荷是一个非定常的复杂载荷，对叶片起着拉—压—弯—扭的综合作用，是喷泵叶轮受到的最主要载荷。

图8 喷泵叶片的有限元网格划分Fig.8 Finite element mesh of impeller

在所有载荷中重力载荷通过指定重力加速度来施加，离心力载荷通过指定叶轮旋转速度施加，而叶片上的压力载荷通过CFD 数值计算得到，即“船体+喷泵+流道”作为一个整体进行流体动力性能的稳态计算，然后以稳态计算结果作为初始值，进行非定常计算，以此得到喷水推进泵流场的压力脉动特性，提取了叶片上的空间脉动压力作为有限元模型的外部载荷。稳态计算结果用于静强度计算，瞬态计算用于计算动强度。

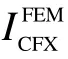
式中：XFEM为有限元节点坐标矩阵；XCFX为流体网格节点坐标矩阵； PjTarget为映射值； PiSource为源项值，Nj为源项节点数，dij为有限元节点与源项节点的欧氏距离[10]。将流体压力加载到有限元网格后的效果图如图10 所示。

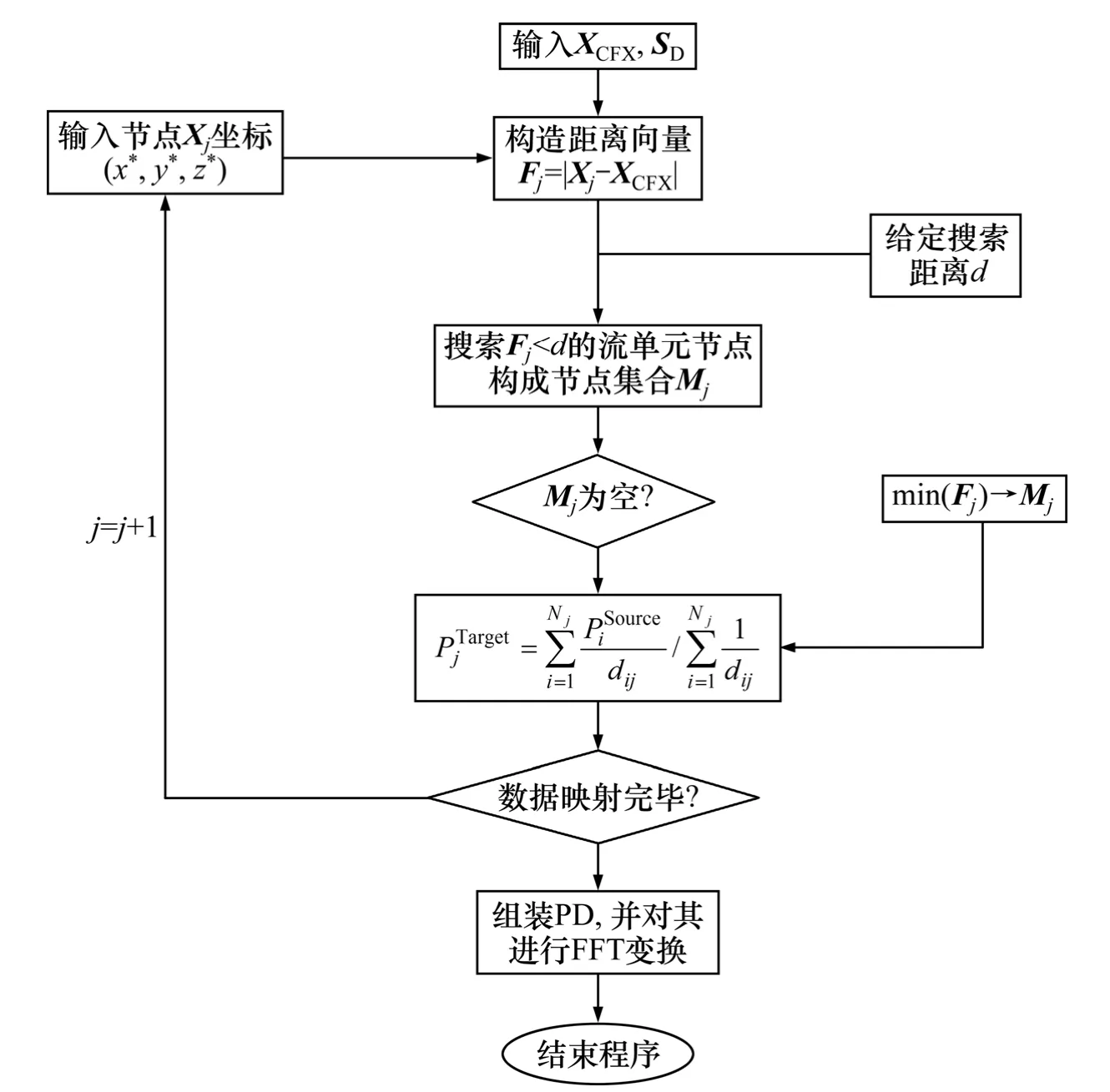
图9 数据映射流程图Fig.9 Flowchart of data projection

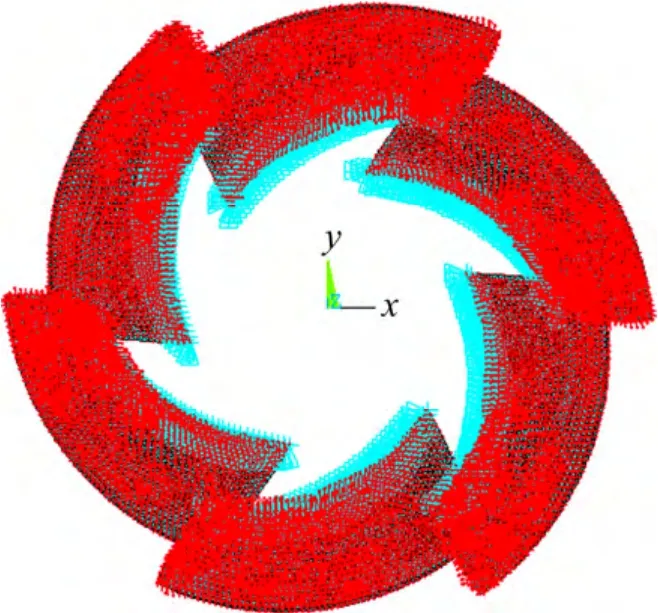
图10 叶轮施加综合载荷后的效果图Fig.10 After applying impeller renderings combined loads

3 计算结果分析

3.1 静强度结果分析

静强度载荷是喷泵在转速880 r/min、船航速74.8 km/h 时计算得到的空间分布载荷。

图11 所示为叶轮在空间分布载荷下的径向位移、周向位移、轴向位移和合成位移云图。由图11 可知：叶片的径向位移、周向位移和轴向位移都呈现出叶片外沿前部附近较大的现象，位移等值线几乎是沿着半径方向向外扩展,并且每个叶片上的变化规律大致一样，呈现较好的规律性。其中，最大径向位移为0.071 mm，最大周向位移为0.092 mm，最大轴向位移为0.113 mm，最大合成位移为0.162 mm。叶片最大径向、周向和轴向位移均出现在叶片的叶顶部前侧，但经过叶片曲面上的空间的相互抵消和叠加作用，使合成的叶片整体位移的最大变形也发生在叶顶部。该型喷水推进泵的叶顶间隙为0.8 mm，各个方向上的变形量均小于叶顶间隙满足要求。

图12 所示为叶轮在综合载荷下的应力云图。分析图12 可知：叶片的最大应力值出现在靠近进口侧的叶片根部。这是因为喷水推进泵叶轮采用的是锥形的轮毂，轮毂的进口侧小于出口侧，于是进口侧至出口侧方向，叶片的径向尺寸逐渐减小。故叶片和轮毂的结合处出现应力集中，最大应力为38.2 MPa，所使用材料的屈服强度为550 MPa，叶片能满足强度要求，如表4 所示。

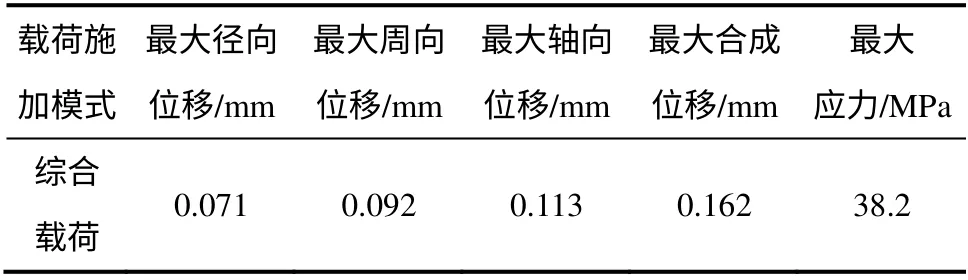
表4 综合载荷下叶片的应力和应变Table 4 Stress and strain under combined loads

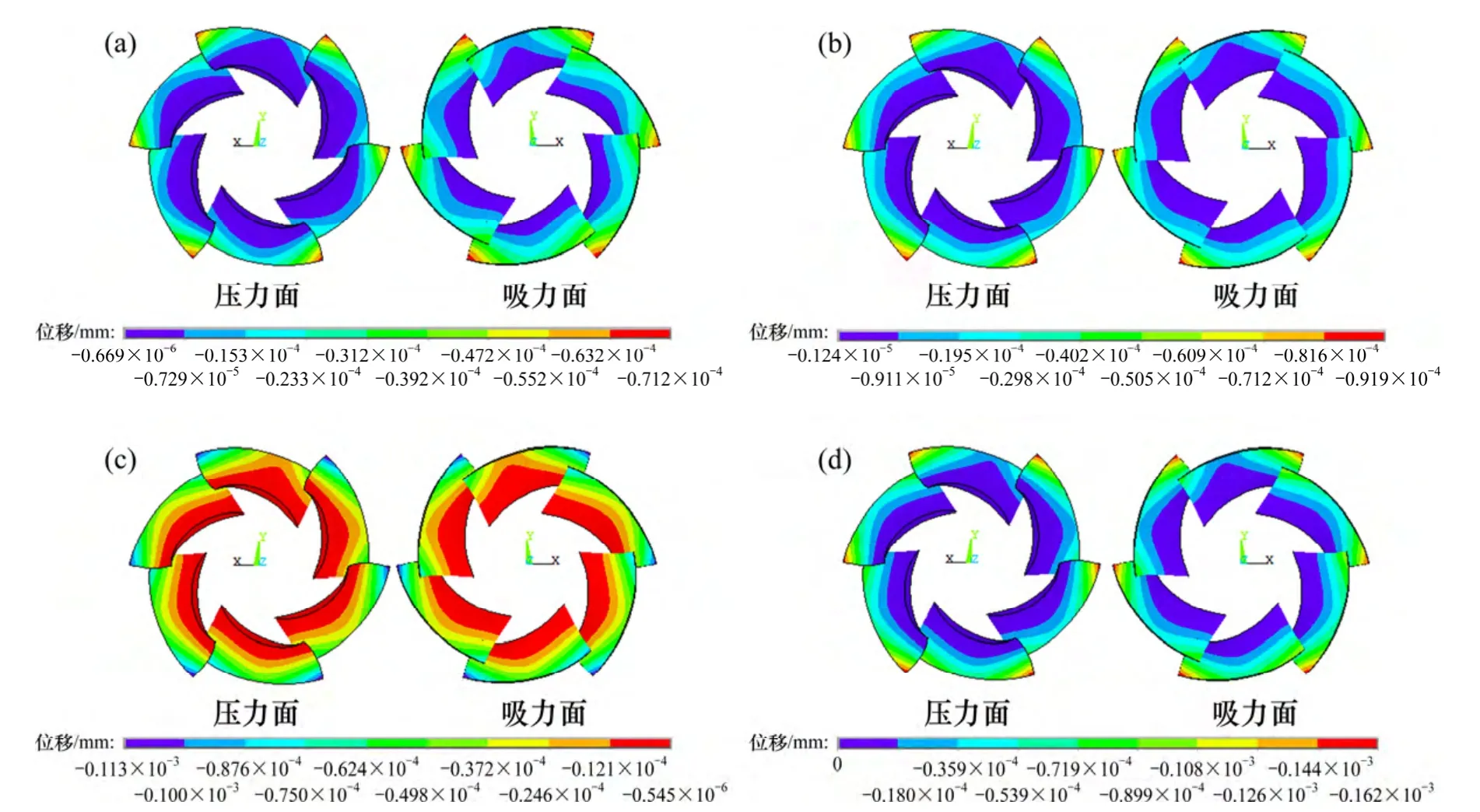
图11 综合载荷下叶片位移云图Fig.11 Displacement contour under combined loads

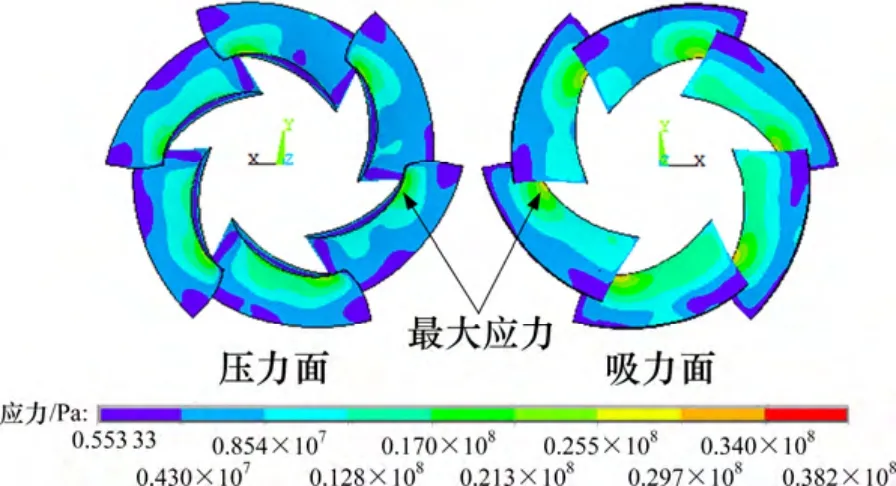
图12 综合载荷下叶片应力云图Fig.12 Stress contour under combined loads

3.2 动强度结果分析

通过CFD 计算出在非定常水动力载荷作用下时叶片旋转360°时的应力、应变情况，设置步距角为1°，分别输出每个角度时叶片的最大径向位移、周向位移、轴向位移和最大应力。对所求出的最大应力、位移作散点图，如图13 和图14 所示。

图13 所示为瞬态载荷作用下叶轮的最大应力变化曲线。分析图13 知不同位置处叶轮的最大应力也不同，且该最大应力都皆位于叶轮根部。另外在叶轮的1 个旋转周期内叶轮的最大应力出现了6 个规律性的脉动，最大峰值为47.69 MPa，最小谷值为45.05 MPa，峰谷值之差达到2.56 MPa，该脉动值与静载荷的最大应力的比值达到(47.69/45.05-1)×100%=5.4%，说明在进行叶轮的强度校核的时有必要分析瞬态载荷作用下的叶轮应力。经计算分析，当叶轮旋转至297°时叶轮的最大应力达到47.69 MPa，小于屈服应力550 MPa，说明动强度满足要求。

图13 瞬态载荷作用下叶轮的最大应力时程曲线Fig.13 Impeller maximum stress curve by transient loads

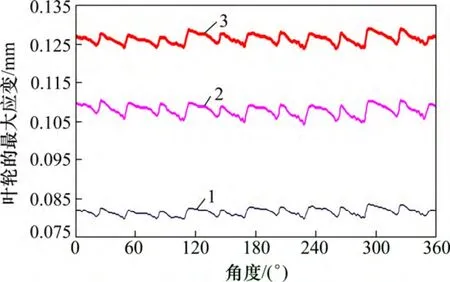
图14 瞬态载荷作用下叶轮的最大变形时程曲线Fig.14 Impeller maximum deformation under transient loads

图14所示为瞬态载荷作用下叶轮叶片3个方向上的最大变形位移曲线。和叶轮的最大应力曲线类似，在叶轮的1 个旋转周期内叶轮的最大变形位移曲线也有6 个规律性脉动。其中轴向位移最大，其平均值为0.126 mm，最大位移为0.129 mm；径向位移次之；周向位移最小；经分析所有变形位移均小于叶轮的叶顶间隙0.8 mm。

分析静强度和动强度结果可知，叶轮因处在不均匀流场中故其载荷和应力是交变的，从应力来看交变的幅值达到(47.69/38.21-1)×100%=24.3%。在理想情况下，叶轮旋转1 周时每个叶轮上的载荷交变1 次，驱动轴上载荷交变6 次；在实际情况下，叶轮交变2次，轴交变12 次。

4 结论

1) 通过FEM 分析得到了叶轮等效应力、等效变形最大值，预测了叶轮最大应力发生部位和最大变形量；利用空间分布力来计算叶轮强度可避免了经典悬臂梁理论不能准确预报叶轮应力分布的问题，对喷泵叶轮的研究和设计有一定的参考意义。

2) 叶轮和轮毂的结合处出现应力集中，叶轮的最大变形出现在叶顶部前侧，为叶轮的设计和改进提供参考和依据。

3) 与静强度计算相比，动强度计算能更准确反映叶片表面的应力和应变情况。但当载荷脉动特性显著时还需要进行疲劳强度计算。

[1] 郑小波, 罗兴, 邬海军. 基于CFD 分析轴流式转轮叶片刚强度分析[J]. 水力发电学报, 2006, 25(5): 121-124.ZHENG Xiaobo, LUO Xing, WU Haijun. Rigidity/strength analysis of the axial flow blades based on CFD[J]. Journal of Hydroelectric Engineering, 2006, 25(5): 121-124.

[2] 吴刚, 王立祥, 张新. 喷水推进轴流泵叶轮强度计算[J]. 农业机械学报, 2009, 40(12): 107-112.WU Gang, WANG Lixiang, ZHANG Xin. Strength calculation of waterjet axial pump impeller[J]. Fluid Machinery, 2009,40(12): 107-112.

[3] 董新国. 混流式喷水推进泵动叶轮、导叶体结构强度分析[D].上海: 上海交通大学机械与动力工程学院, 2011: 1-100.DONG Xinguo. Static strength analysis of impeller of mixed flow waterjet pump[D]. Shanghai: Shanghai Jiao Tong University, School of Mechanical Engineering, 2011: 1-100.

[4] Katsutoshi K. Prediction of stress on pump blade by one-way coupled method of fluid and structure simulation[C]//Proceeding of IMECE2007. Washington, USA, 2007: 1-7.

[5] Katsutoshi K, Shimizu H, Shigenaga Y. Prediction of unsteady hydraulic force in a mixed-flow pump with volute casing by using large eddy[C]//38th Asian International Fluid Machinery Conference. Yichang, China, 2005: 1-7.

[6] Lerche A, Moore J J, Yusheng F. Computation modeling and validation testing of dynamic blades stress in a rotating centrifugal compressor using a time domain coupled fluid-structure computation model[C]. Proceedings of ASME Turbo Expo 2010. Glasgow, UK, 2007: 1-8.

[7] Benra F K. Numerical and experimental investigation on the flow induced oscillations of in a single blade pumps impellers[J].Journal of Fluid Engineering, 2006(128): 783-793.

[8] 常书平, 王永生. 采用k-ε 湍流模型的喷水推进器性能预报[J]. 华中科技大学学报(自然科学版), 2012, 40(4): 88-90.CHANG Shuping, WANG Yongsheng. Prediction of waterjet performances using k-ε turbulence models[J]. Journal of Huazhong University of Sience and Technology: Nature Sience Edition (Nature Science Edition), 2012, 40(4): 88-90.

[9] 刘承江, 王永生, 张志宏. 喷水推进器数值模拟所需流场控制体的研究[J]. 水动力学研究与进展(A 辑), 2008, 23(5):592-595.LIU Chengjiang, WANG Yongsheng, ZHANG Zhihong. Study on flow control volume in numerical simulation of waterjet propulsor[J]. Chinese Journal of Hydrodynamics (A), 2008,23(5): 592-595.

[10] 魏应三, 王永生. 基于声场精细积分算法的潜艇流噪声预报[J]. 计算力学学报, 2012, 29(4): 574-580.WEI Yingsan, WANG Yongsheng. Flow-excited submarine structure acoustic prediction based on a refined integral algorithm[J]. Chinese Journal of Computational Mechanics,2012, 29(4): 574-580.