疲劳荷载作用下部分预应力混凝土梁裂缝宽度计算模型

韩基刚，宋玉普，常继峰

(1. 大连理工大学 建设工程学部，辽宁 大连，116024；2. 辽宁省交通规划设计院，辽宁 沈阳，110166；3. 哈尔滨学院 工学院，黑龙江 哈尔滨，150086)

众所周知，B 类部分预应力混凝土(partially prestressed concrete，PPC)梁作为桥梁和海洋平台等工程中较为常见的一种结构形式，在承受静力荷载的同时还需要承受疲劳荷载的作用。随着疲劳循环次数的增加，梁体裂缝不断扩展。当裂缝宽度达到一定程度时，不仅影响结构的美观，而且可导致梁内钢筋锈蚀，从而降低结构的耐久性。因此，现有设计规范均对梁体裂缝进行验算和控制[1-2]，其中疲劳裂缝宽度的准确预测是进行合理疲劳设计的前提。然而，通过现有PPC梁疲劳裂缝宽度计算公式得到的结果尚存在不小的差异，仍有待进一步研究。近年来，国内外学者进行了大量的PPC梁疲劳试验，以期得到裂缝宽度扩大系数，进而估算不同疲劳荷载作用次数下梁的裂缝宽度[3-5]。但由于采用试验梁的尺寸、截面类型、配筋形式和混凝土强度等因素的影响，不同研究者得到的扩大系数并不相同，甚至相差几倍，这使其在实际工程设计应用中具有一定的局限性，因此，针对疲劳荷载作用下PPC 梁裂缝宽度的计算方法需要进行必要的理论分析。目前，有关PPC 梁疲劳裂缝宽度的理论计算模型均以黏结-滑移理论为基础，并考虑了混凝土的循环徐变、梁弯曲刚度退化、滑移的增大以及混凝土收缩的影响[6-7]。然而，上述计算模型中却忽略了以下2个重要问题：1) 未考虑疲劳荷载作用下，梁内非预应力钢筋与混凝土之间的黏结应力-滑移退化关系，从而低估了梁的裂缝开展宽度。2) 非预应力钢筋应力是确定PPC 梁裂缝宽度的最重要参数[7-8]，但已有开裂截面应力计算方法并未考虑疲劳荷载作用下，因预应力与非预应力钢筋之间黏结性能的不同而产生的钢筋应力重分布以及非预应力钢筋残余应变对钢筋应力的影响[9-10]，这会导致采用相应方法计算得到的开裂截面非预应力钢筋应力偏小。为了更加合理地考虑上述因素的影响，本文作者建立非预应力钢筋与混凝土之间的疲劳黏结应力-滑移关系，给出合理非预应力钢筋应力计算方法，在此基础上，提出PPC 梁疲劳裂缝宽度数值计算模型，并通过6 根PPC 梁的试验数据验证模型的准确性。

1 非预应力钢筋与混凝土之间疲劳黏结应力-滑移关系

1.1 静载作用下黏结应力-滑移关系

在疲劳荷载作用下，钢筋与混凝土之间的黏结性能不断发生退化，表现为黏结强度的降低和滑移的增大。显然，静载作用下的钢筋与混凝土之间的黏结应力-滑移关系已不再适用。因此，本文首先建立了钢筋与混凝土之间的疲劳黏结应力-滑移关系。

在静载作用下，钢筋和混凝土之间的黏结应力-滑移关系模型[11]为

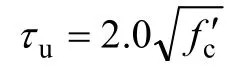
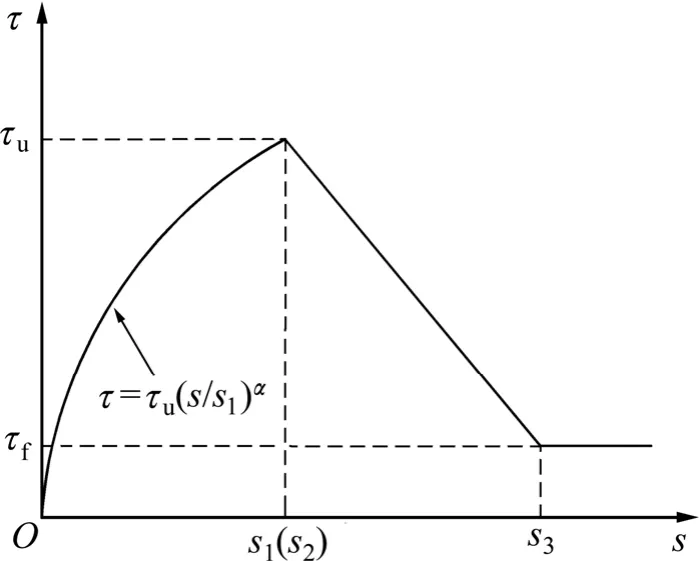
图1 静载作用下黏结应力-滑移关系Fig.1 Bond stress-slip relationship under static loading

1.2 疲劳剩余黏结强度及包络线

疲劳剩余黏结强度是指在一定次数疲劳荷载作用后，钢筋与混凝土界面上还能承受的最大黏结应力。而疲劳剩余黏结强度包络线则是指经历任意次数疲劳加载后的疲劳黏结剩余强度与疲劳加载次数之间的关系曲线。

通过分析疲劳荷载作用下钢筋与混凝土之间的黏结应力-滑移变化曲线如图2 所示。由图2 可知：发生疲劳黏结破坏时的最大滑移与静载作用下得到的黏结应力-滑移曲线下降段最大黏结应力所对应的滑移相当[12-13]。因此，本文近似以静载作用下黏结应力-滑移曲线下降段代替疲劳荷载作用下剩余黏结强度包络曲线，如图3 所示。

参考静载作用下的黏结应力-滑移关系曲线，并结合疲劳剩余强度包络线(图3)，可得到疲劳剩余强度包络线方程：

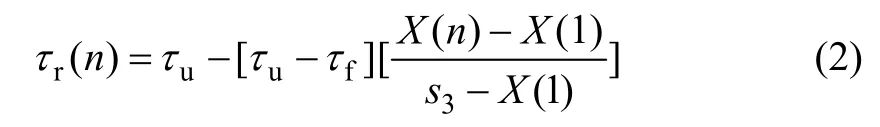
其中：τr(n)为n 次循环加载次数后的剩余黏结强度。

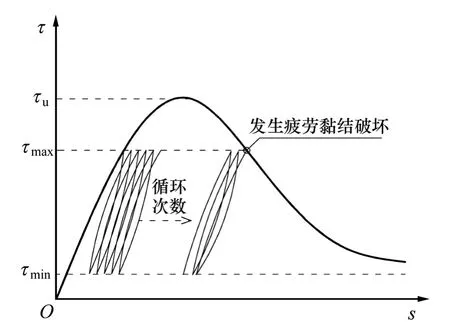
图2 随循环次数增加的黏结应力-滑移变化曲线[12]Fig.2 Evolution of bond stress-slip with number of cycles[12]

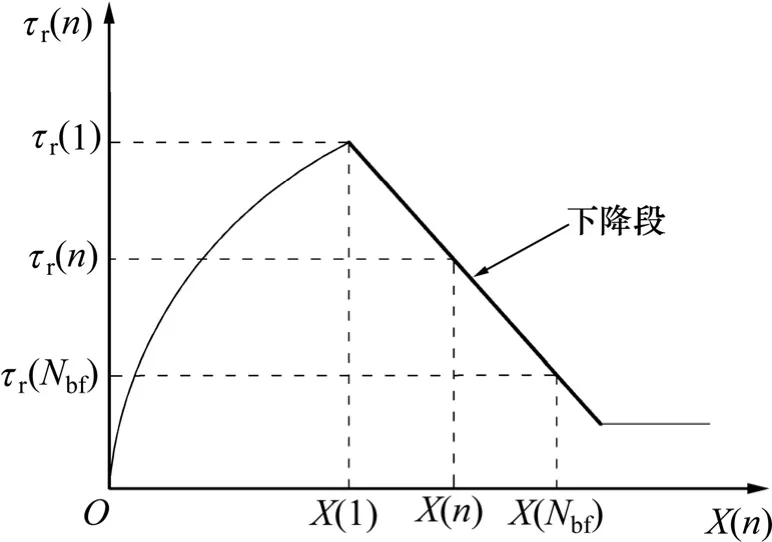
图3 疲劳剩余强度包络线Fig.3 Envelope curve of fatigue residual bond strength

定义X(n)为与疲劳加载次数n 有关的函数，从而有

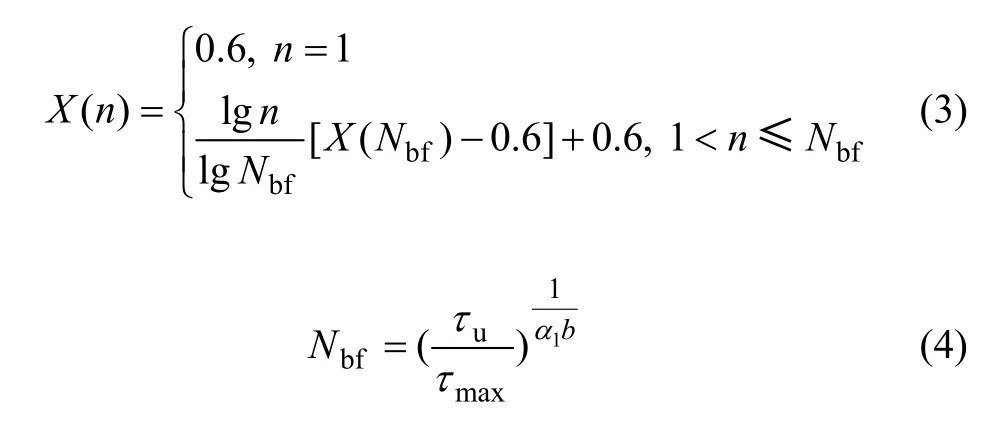
式中：n 为任意循环次数；Nbf为钢筋与混凝土之间发生疲劳黏结破坏时所对应的疲劳寿命[14]；τmax为最大黏结应力，α1=0.5， b=0.057。

在等幅疲劳黏结应力作用下，黏结退化过程可看作疲劳黏结剩余强度不断衰减的过程。当疲劳剩余黏结强度衰减到等幅最大黏结应力(τmax)时，可认为钢筋与混凝土之间发生疲劳黏结破坏，即τr(Nbf)=τmax，而寿命期内各疲劳加载次数下的疲劳剩余黏结强度可通过插值函数曲线求得，同时该函数曲线必须满足相应的边界条件，由此得到的函数曲线方程即为疲劳剩余强度包络线方程。

由边界条件可知：当n=1 时，X(1)=0.6，τr(1)=τu；当n=Nbf，τr(Nbf)=τmax。将已知边界条件代入式(2)，可求得X(Nbf)：

综上所述，可求得任意循环次数后的疲劳剩余黏结强度为

定义任意加载次数后的极限黏结强度损伤因子(Dn)为

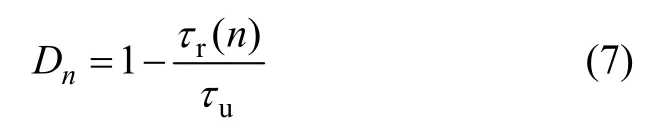
1.3 任意疲劳加载次数后黏结应力-滑移关系

蒋德稳等[14-15]按照相同的试验方法进行了重复荷载作用下的拉拔试验，得到了变形带肋钢筋与混凝土之间的黏结滑移变化规律，并以CEB-FIP 90 规范给出的黏结应力-滑移关系曲线的上升段为基础，提出了考虑残余滑移的幂函数形式疲劳黏结应力-滑移关系，其中通过引入试验系数(αn)来考虑应力水平和重复次数的影响。所不同的是：文献[14]采用的试样锚固长度比文献[15]中的长，所得到的相应试验系数更能反映工程实际，因此，本文采用文献[14]提出的上升段疲劳黏结应力-滑移关系式及相关试验系数：

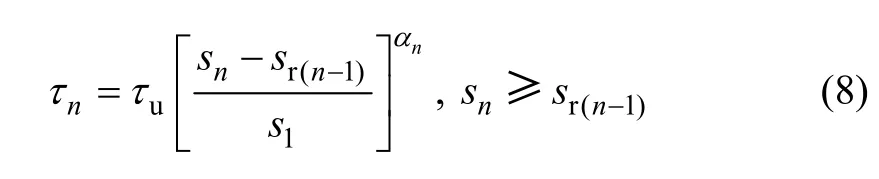
式中：sr(n-1)为第n-1 次重复加载后的残余滑移，可按照式(9)和(10)计算；sn为第n 次重复加载后的滑移；αn为试验系数，可按照式(11)计算。

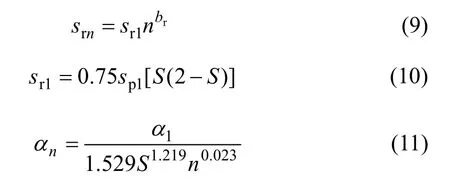
式中：S 为重复荷载的应力水平，S=τmax/τu；sr1为第1次重复加载后的残余滑移；srn为第n 次加载后裂缝处的残余滑移；sp1为第1 次重复加载后的滑移；br=0.057；α1=0.5。

实际上，在黏结长度范围内，残余滑移在不同的位置(x)处是变化的，目前关于此方面的研究较少，而文献[14]仅给出加载端的残余滑移计算公式。为了得到不同位置处的残余滑移，本文假设其在黏结长度范围内符合线性分布，且具有对称性，如图4 所示，从而近似得到相应的残余滑移(srn,x)为

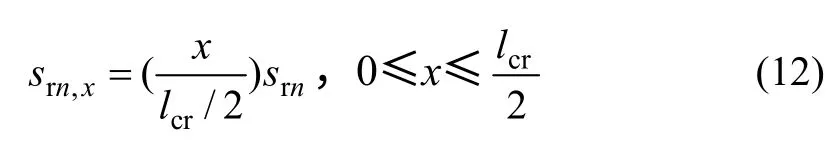
式中：lcr为裂缝间距。

图4 沿黏结长度滑移和残余滑移分布图Fig.4 Distribution of slip and residual slip along bond length

另外，需要指出的是：文献[14]只给出了疲劳荷载作用下上升阶段黏结应力-滑移关系，且未考虑因疲劳荷载作用而导致极限黏结强度降低的影响。为了得到疲劳荷载作用下的全阶段黏结应力-滑移关系，本文首先假定残余强度随极限强度呈比例降低，同时与残余强度相对应的特征滑移量并不随荷载循环次数的增加而变化；然后以静载作用下黏结应力-滑移关系为基础，综合考虑疲劳荷载作用下极限黏结强度降低和残余滑移增大的影响，并引入极限黏结强度损伤因子，从而建立任意疲劳加载次数后的非预应力钢筋与混凝土之间的疲劳黏结应力-滑移关系曲线，如图5所示，具体表达式如下：

图5 疲劳黏结应力-滑移关系曲线Fig.5 Fatigue bond stress-slip relationship

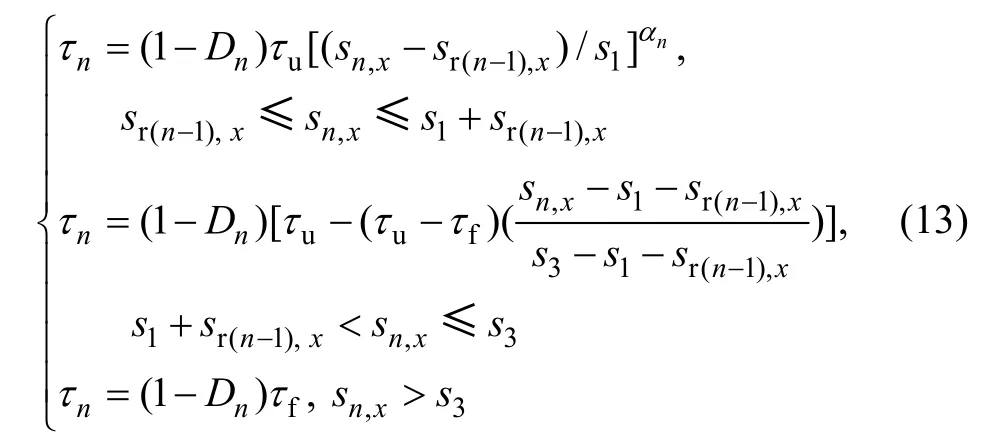
式中：sn,x为第n 次循环加载后的不同位置x 处的滑移；sr(n-1),x为第n-1 次循环加载后的不同位置x 处的残余滑移，按照式(12)计算。

2 疲劳裂缝宽度计算模型

2.1 裂缝间距计算

已有试验表明，PPC 梁在经历一定疲劳荷载作用后，在纯弯段内的裂缝已不再产生，裂缝间距变化较小。因此，假定PPC 梁的裂缝开展均已处于稳定阶段，且裂缝间距并不随荷载循环次数的增加而增大，此时裂缝间距(lcr)可按照文献[2]给出的公式计算：

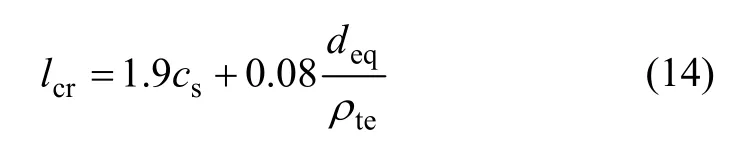
式中：cs为最外层纵向受拉钢筋外边缘至受拉区底边的距离；deq为受拉区纵向钢筋的等效直径；ρte为按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率。有效受拉混凝土面积(Ate)为

式中：b 为矩形截面宽度、T 形或I 形截面腹板宽度，h 为梁高；bf和hf分别为受拉翼缘的宽度和高度。

2.2 钢筋与受拉区混凝土平衡关系

在裂缝间距范围内任取一距离为dx 的微单元(见图6)，相应的有效受拉区应力传递如图7 所示。

根据力的平衡条件可知：

图6 梁裂缝Fig.6 Beam crack

图7 单元应力平衡Fig.7 Stress equilibrium of element

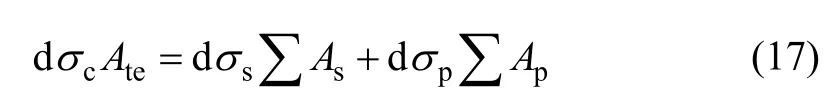
式中：As和∑ As分别为非预应力的钢筋面积和总面积；Ap和∑ Ap分别为预应力钢筋的面积和总面积；dσs和dσp分别为非预应力钢筋应力增量和预应力钢筋应力增量；dσc为受拉区混凝土应力增量；τs和τp分别为非预应力钢筋黏结应力和预应力钢筋黏结应力；ds和dp分别为非预应力钢筋直径和预应力钢筋直径。由式(16)可知：

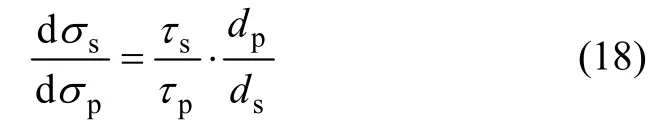
令ζ=τp/τs；由于不同类型钢筋沿黏结长度范围内黏结应力分布图近似，为了简化计算，假设在疲劳荷载作用过程中，非预应力钢筋与预应力钢筋在不同位置处的非预应力钢筋和预应力钢筋黏结应力比值不变，本文ζ 值按照CEB-FIP 90 规范中给出的相对黏结系数取用[11]，该规范建议对于后张PPC 梁，当采用钢绞线作为预应力钢筋时，ζ=0.4。

将式(18)代入式(17)可得

因此，有

2.3 裂缝宽度计算

梁开裂后，非预应力钢筋与混凝土之间存在应变差异，从而产生相对滑移(ds/dx)，两者存在如下等式：

式中：εs为非预应力钢筋应变；εc为混凝土应变；εsh为混凝土收缩应变，可近似取收缩应变极限值0.000 6[16]。

假设在正常使用状态下，裂缝之间混凝土和非预应力钢筋均处于弹性阶段，从而有

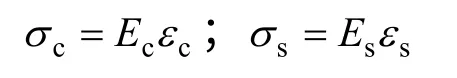
由边界条件可知：开裂截面处，σs=σs,n； σc=0；在两条相邻裂缝之间的跨中截面处，s=0。其中：σs和σc分别表示非预应力钢筋和混凝土应力；Ec和Es分别表示混凝土和非预应力钢筋弹性模量；s 为钢筋与混凝土之间的相对滑移；σs,n为疲劳荷载作用下，计算得到的开裂截面处的非预应力钢筋应力。

根据黏结-滑移理论，裂缝开展正是钢筋与混凝土之间的相对滑移增大所致，因此，当利用式(21)和相应边界条件求得开裂截面处的非预应力钢筋与混凝土之间的相对滑移(scr)时，PPC 梁的裂缝宽度(W)可通过下式计算：

2.4 单元的基本关系式

在纯弯段内，选取长度为lcr/2 的梁体作为研究对象，并以相邻裂缝之间的跨中截面位置处作为起始点，划分k-1 个距离为Δx 的单元，如图8 所示。

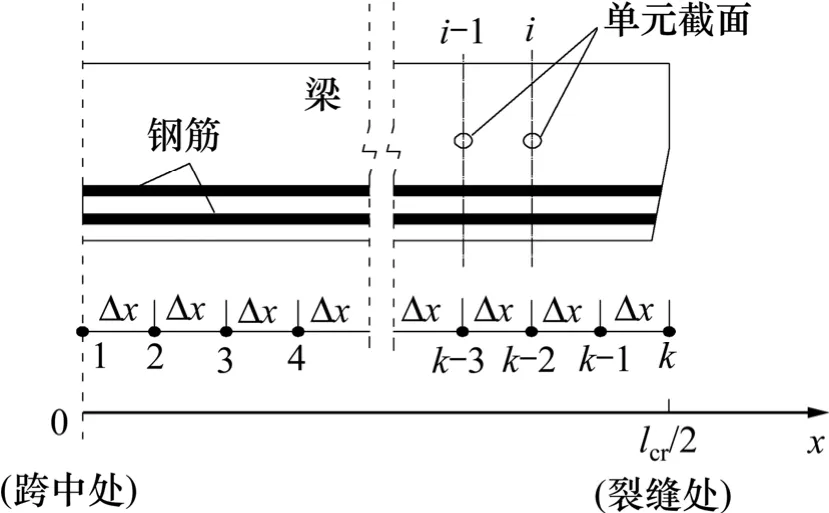
图8 单元划分示意图Fig.8 Schematic diagram for dividing elements

对于任意单元而言，相邻单元截面i 和i-1 的非预应力钢筋应力、有效受拉区混凝土应力和非预应力钢筋与混凝土之间的相对滑移存在如下等式：

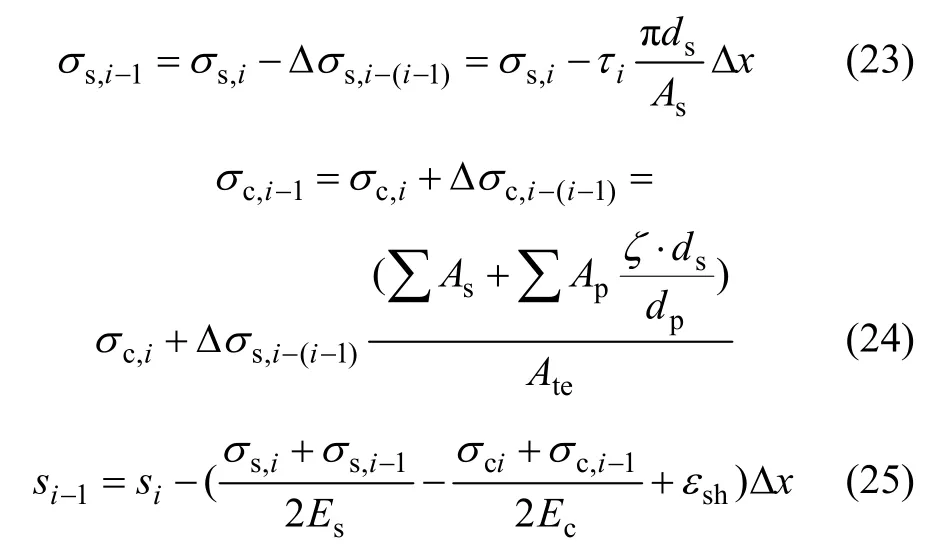
2.5 非预应力钢筋应力计算方法

对于PPC 梁，随着疲劳加载次数的增加，梁的弯曲刚度不断退化，受压区混凝土和钢筋残余应变不断增大，不同类型受拉钢筋之间产生了钢筋应力重分布，这都将导致梁内钢筋应力增大。显然，为了合理计算PPC 梁的非预应力钢筋应力，以上因素均应考虑。

首先基于文献[17]提出的预应力混凝土梁受弯构件疲劳损伤全过程非线性分析方法，可求得任意循环荷载作用次数下，PPC 梁开裂截面处的非预应力钢筋应力和预应力钢筋应力增量，该方法考虑了受压区混凝土残余应变、弯曲刚度退化以及受拉钢筋面积损失对钢筋应力的影响。由于在文献[17]给出的方法中，其所采用的混凝土残余应变计算公式并未考虑时间因素的影响，因此，本文中的混凝土残余应变可按文献[6]建议的公式计算：

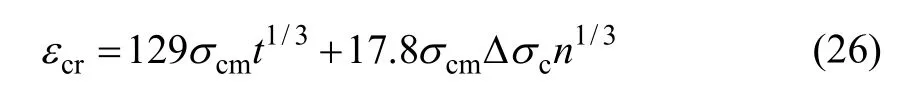
式中：t 为荷载作用时间；n 为循环荷载作用次数；σcm为混凝土平均应力比；Δσc为混凝土应力幅值；σcm和Δσc可通过受压区混凝土的最大应力(σc,max)、最小应力(σc,min)和混凝土抗压强度(fc)求得：

由文献[9]可知，疲劳荷载作用将导致梁内受拉钢筋与混凝土之间的黏结性能不断退化，同时由于非预应力和预应力钢筋之间黏结性能不同，使得开裂PPC梁的不同类型受拉钢筋之间存在应力重分布现象。为了考虑其对钢筋应力的影响，可通过现有开裂截面分析方法，并引入钢筋应力分配系数(ξ)来计算开裂截面钢筋应力[9]，相应的钢筋应力分配系数表达式可定义为

此时，存在如下等式：

将式(29)代入式(30)可求得考虑不同类型钢筋黏结性能差异情况下，产生应力重分布后的非预应力钢筋应力为

试验研究表明[10,18]：PPC 梁在疲劳荷载作用下梁内非预应力钢筋将产生残余应变，并随着疲劳荷载次数的增加，而不断增大。文献[10]基于6 片PPC 梁的试验数据回归得到了梁内非预应力钢筋残余应变随循环次数变化规律，相应回归公式表示如下：

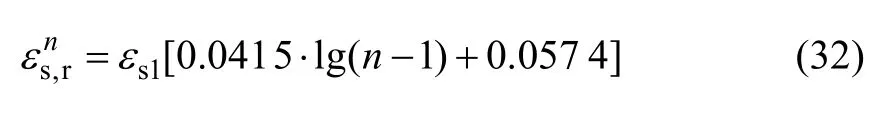
综上所述，在综合考虑梁弯曲刚度退化、不同类型受拉钢筋之间的应力重分布和残余应变等因素影响时，疲劳荷载作用下PPC 梁开裂截面非预应力钢筋应力(σs,n)为

2.6 疲劳荷载下部分预应力混凝土梁裂缝宽度计算流程

按照以上理论研究，通过Visual Basic 语言编制计算程序，从而得到不同疲劳加载次数下PPC 梁的裂缝宽度，相应的迭代过程和计算流程图见图9。

图9 裂缝宽度计算流程图Fig.9 Flow chart of crack width solution

3 计算模型试验验证

3.1 试验

为了研究疲劳荷载作用下PPC梁裂缝宽度的变化状态，进行了8 根PPC 梁的疲劳试验。根据预应力比率和配筋形式的不同，将试验梁分为2 组(H1 组和H2组)，每组梁均采用相同的配筋和预应力比率，且各组均有1 根进行静载试验，其余试验梁进行等幅疲劳试验。试件的外形尺寸、详细配筋情况及加载设置见图10。

梁内非预应力钢筋采用直径为14 mm 和16 mm的HRB400 级钢筋，相应的屈服强度分别为442 MPa和413 MPa；预应力钢绞线采用1860 级7 股钢绞线，张拉控制应力为1 302 MPa；箍筋和架立筋均采用HPB234 级光圆钢筋，箍筋间距如图10(a)所示。各试验梁实测混凝土抗压强度、加载参数和试验结果如表1 所示。

图10 试验梁设计和加载设置(单位：mm)Fig.10 Design of test beams and loading arrangement

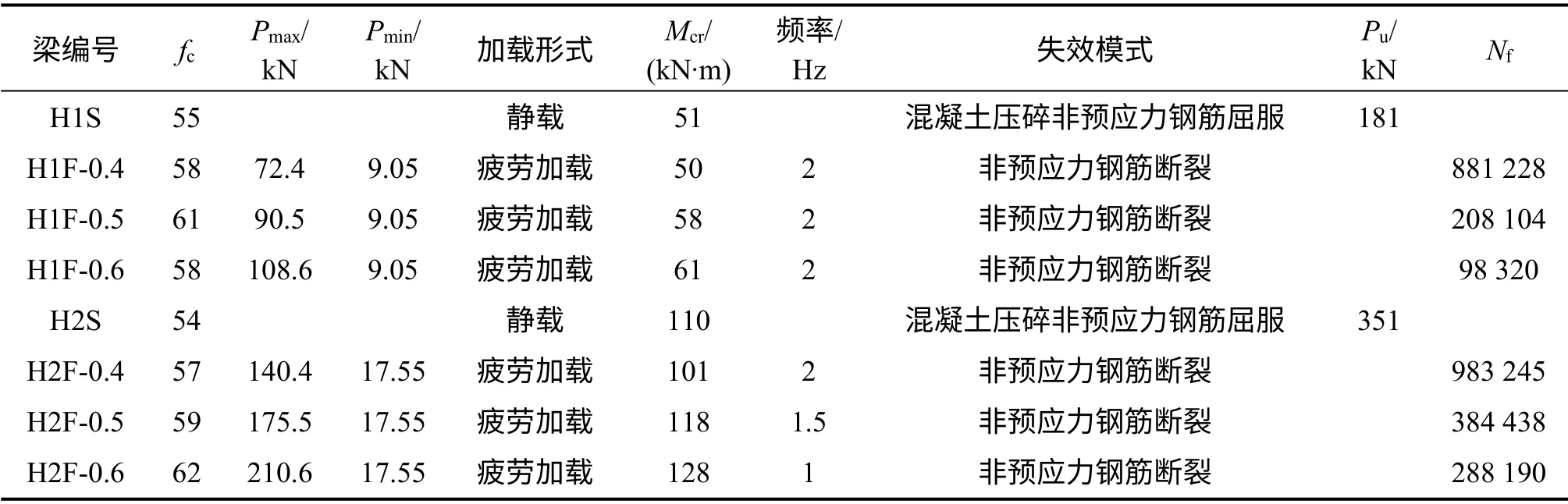
表1 混凝土抗压强度、加载参数和试验结果Table 1 Concrete compressive strength,load parameter and test results

静载以及疲劳试验均在1 MN 的MTS 疲劳试验机上进行，在疲劳试验过程中，当循环次数达到预定次数时，停机加静载至最大荷载，用裂缝观测仪测量各条裂缝在非预应力钢筋重心对应的梁侧面处的裂缝间距和裂缝宽度。

3.2 模型计算值与试验结果对比分析

利用本文编制的计算程序以及文献[3]和[8]所给出的疲劳裂缝宽度计算方法分别得到了各试验梁在预定循环次数下的裂缝宽度，计算结果与试验值对比如图11 所示。

从图11 可以看出：按照文献[3]的方法计算得到的最大裂缝宽度随着循环次数的增加，与试验结果的差异不断增大；对于应力水平较小的试验梁，按照文献[8]的方法计算得到的最大裂缝宽度与试验结果偏差较大(见图11(a)和11(b))，而采用本文所提出的疲劳裂缝宽度模型计算的裂缝宽度与试验结果较吻合，随循环次数的变化规律与试验结果相似。此外，对于配筋率较低的H1 组梁而言，相应的模型计算值较试验数据相对保守，因此，该模型可作为PPC 梁的抗疲劳设计和验算参考。

图11 裂缝宽度试验值与计算值对比Fig.11 Comparison between experimental values and calculation values of crack width

4 结论

1) 以静载作用下钢筋与混凝土之间的黏结应力-滑移关系为基础，并考虑疲劳荷载作用下极限黏结强度降低，残余滑移增大的影响，建立了非预应力钢筋与混凝土之间的疲劳黏结应力-滑移关系。

2) 综合考虑非预应力钢筋与预应力钢筋之间的钢筋应力重分布、混凝土和非预应力钢筋残余应变以及受拉钢筋面积损失，给出了一种开裂截面非预应力钢筋应力计算方法。

3) 基于黏结滑移理论，引入疲劳黏结应力-滑移关系，建立了PPC 梁疲劳裂缝宽度计算模型，计算结果与试验结果吻合较好，从而验证了疲劳黏结应力-滑移关系的适用性和计算模型的有效性。

[1] JTJ D62—2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].JTJ D62—2004,Code for design of highway reinforced concrete and prestressed concrete bridges and culverts[S].

[2] GB 50010—2010, 混凝土结构设计规范[S].GB 50010—2010,Code for design of concrete structures[S].

[3] 卢树圣, 欧忠洪. 重复荷载作用下PPC 梁裂缝的研究及其计算模式的分析[J]. 长沙铁道学院学报,1991,9(3):121-131.LU Shusheng, OU Zhonghong. Investigation on the crack of PPC beam under repeated loading and analysis of its calculating model[J]. Journal of Changsha Railway University, 1991, 9(3):121-131.

[4] Bennett E W, Dave N J. Test performances and design of concrete beams with limited prestress[J].The Structure Engineer,1969,47(12):487-499.

[5] 章坚洋, 宋玉普, 章一涛. 混合配筋部分预应力混凝土梁在疲劳荷载下的裂缝宽度计算[J]. 混凝土,2005(12):21-24.ZHANG Jianyang, SONG Yupu, ZHANG Yitao. Calculation of the crack width for PPC beam with non-prestressed steel and prestressed tendons[J].Concrete,2005(12):21-24.

[6] Balaguru P N. Analysisi of prestressed concrete beams for fatigue loadin[J].PCI Journal,1981,16(5):22-52.

[7] Harajli M H, Naaman A E. Cracking in partially prestressed beams under static and cyclic fatigue loading[J]. ACI Special Publication,1989,113:29-54.

[8] Shahawi M E I, de Batchelor V. Fatigue of partially prestressed concrete[J]. Journal of Structural Engineering, 1985, 112(3):524-537.

[9] 冯秀峰, 宋玉普, 章坚洋, 等. 疲劳荷载下预应力混凝土梁中钢筋应力重分布的试验研究[J]. 建筑结构学报, 2006,27(2):94-99.FENG Xiufeng, SONG Yupu, ZHANG Jianyang, et al.Experimental study on stress redistribution of reinforcing steel in prestressed concrete beams under fatigue loading[J]. Journal of Building Structures,2006,27(2):94-99.

[10] 钱永久. 疲劳荷载作用下部分预应力混凝土梁的裂缝控制[J].西南交通大学学报,1987(4):104-109.QIAN Yongjiu. Crack control for partially prestressed concrete beams under fatigue loading[J]. Journal of Southwest Jiaotong University,1987(4):104-109.

[11] CEB-FIP,CEB-FIP Model Code 1990[S].

[12] Balazs G L. Fatigue of bond[J]. ACI material journal, 1991,88(6):620-629.

[13] Zanuy C,Albajar L,de la Fuente P.On the cracking behaviour of the reinforced concrete tension chord under repeated loading[J].Materials and Structures,2010,43(5):611-632.

[14] 蒋德稳, 邱洪兴. 重复荷载下钢筋与混凝土黏结本构关系[J].工程力学,2012,29(5):93-100.JIANG Dewen, QIU Hongxing. Bond-slip basic constitutive relation model between rebar and concrete under repeated loading[J].Engineering Mechanics,2012,29(5):93-100.

[15] Oh B H, Kim S H. Realistic models for local bond stress-slip of reinforced concrete under repeated loading[J]. Journal of Structural Engineering,2007,133(2):216-224.

[16] 陈颐, 吕东莉. 关于新《桥规》中混凝土收缩应变的讨论[J].公路,2006,10(10):49-51.CHEN Yi, LU Dongli. Discussion about concrete shrinkage strain introduced in new china code for RC and PC bridges and culverts[J].Highway,2006,10(10):49-51.

[17] FENG Xiufeng, SONG Yupu, ZHU Meichun. Fatigue damage modeling for partially prestressed concrete beams under repeated loading with variable amplitude[J]. Journal of Southwest Jiaotong University,2006,14(3):258-264.

[18] 钟明全, 车惠民, 邵小康. 部分预应力混凝土梁的非预应力钢筋应力状态研究[J]. 重庆交通学院学报,1993,12(1):1-6.ZHONG Mingquan, CHEN Huimin, SHAO Xiaokang.Investigation on the stress state in non-prstressed steel in prestressed concrete beams[J]. Journal of Chongqing Jiaotong Institute,1993,12(1):1-6.