基于物理模拟试验的库岸滑坡冲击涌浪
2014-04-01肖莉丽殷坤龙王佳佳刘艺梁
肖莉丽,殷坤龙,王佳佳,刘艺梁
(中国地质大学(武汉) 工程学院,湖北 武汉,430074)
随着各个大小水电站在我国的建成,库岸滑坡涌浪灾害也越来越受到人们的关注。库岸滑坡以一定速度滑入水中后往往会激起不同形态、具有一定能量的水体雍高,并随着能量的消散逐渐向远处传播,这个过程即为滑坡涌浪,它包括了近源区产生的冲击涌浪、沿河道传播的传播浪以及冲向两岸的爬坡浪。由于滑体类型众多且所处的地质环境相差甚异,国内外众多学者针对不同的类型的涌浪开展了物理试验设计和经验公式研究。例如,国外学者Slingerland 等[1]基于某工程实例的模型试验,得出了最大涌浪高度与无量纲动能之间的经验公式;Fritz 等[2-3]基于二维水槽试验,分析了涌浪引起的流场特点,通过大量模型试验总结出最大涌浪高度及能量传递公式;van der Meer 等[4]考虑了爬坡方位角、平台影响系数和边坡表面粗糙率等因素,提出了不同类型的波浪爬高公式;Walder等[5]研究了滑坡入水后近水域的波长和波幅的经验公式;Ataie-Ashtiani 等[6]基于室内的120 组试验数据,得到了涌浪波幅和周期的经验公式,并用前人的试验数据验证了其合理性;国内学者潘家铮[7]对水平和垂直方向滑动的滑坡最大涌浪高度进行了分析,并得到了涌浪的经验计算公式;汪洋[8]利用解析法提出了上下游爬坡浪高的估算公式;殷坤龙等[9]以三峡库区典型滑坡及河道为原型,进行了滑坡涌浪物理模拟,提出了适用于三峡库区滑坡冲击涌浪中首浪的经验公式。然而,多数学者在研究滑坡入水的冲击涌浪时,都只注重了涌浪中一种水体雍高的研究。研究发现,在一定的试验条件下,不同水体雍高所指代的内容并不相同,因此,有必要用一种更全面的方式描述滑坡冲击涌浪的形态特征,以避免在实际应用中混淆滑坡涌浪的概念,造成后续计算结果的一系列误差。从水体雍高的形态来看,高速入水的滑坡产生的初始涌浪一般包括散体浪花、可以向对岸方向飞跃的舌状水波(即水舌)以及可以向远处传播的实体水波(即首浪)。散体浪花携带能量小且不能向远处传播,不足以造成灾害,因此在研究中一般不做考虑;水舌和实体水波都是携带一定能量并具有一定传播距离的水体,都可能威胁到影响范围内的居民生命及财产安全。其中水舌的产生时间极短,影响范围小,经常容易被忽略。然而在山区深切峡谷型的河道中发生的大型滑坡,由于河面比较狭窄,其涌浪往往是在首浪还没有完全形成时就已经到达了对岸,此时的水舌会直接飞跃拍打至对岸,而且其拍打的高度远大于水波到达的高程,其携带的能量在对岸释放也足以对承灾体造成巨大的危害,因此,对水舌的研究也是冲击涌浪研究中必不可少的部分。在此,本文作者介绍了滑坡涌浪三维物理
试验的试验条件及设计;根据试验观测结果明确提出了冲击涌浪的概念;对冲击涌浪中的水舌和首浪进行了试验数据分析,以水舌的最大高度η′和水舌长度S作为2 个基本特征量,依据试验数据拟合η′和S 的经验公式;根据水舌运动过程中的受力条件,提出了以抛物线方程形式的水舌运动轨迹方程,可以预测不同宽度的河道中水舌运动至对岸的最高点位置;阐明了水舌与首浪的关系;最后,选取三峡库区大堰塘滑坡和千将坪滑坡为实例,应用本文提出的理论公式进行涌浪预测分析,验证了公式具有较好的适应性和较高可靠性。
1 试验设计
1.1 相似条件
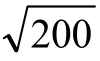
1.2 试验方案设计
本实验为三维滑坡涌浪物理模拟试验,主要以三峡库区的库岸滑坡为研究对象,选取滑坡体长度l、宽度w、厚度t、滑坡入水速度v、滑坡入水处最大水深h、滑动面倾角α、滑坡入水断面的河道宽度b 作为滑坡冲击涌浪的影响因素。通过分析三峡库区进行专业监测的122 个滑坡的长度、宽度、厚度、下滑速度、不同库水位工况下水深及岸坡坡角的分布特点,选取了其水平值(表1)。按照正交试验设计方法,选用L49(76)正交表,按照相似比为1:200 的比例尺制定试验方案,共进行49 组147 次试验,每组试验做3 次,取平均值为试验分析数据。
1.3 涌浪控制系统及观测系统
滑坡入水速度是试验中需要准确控制的变量。速度的控制通过滑速控制设备完成,主要是调节滑坡在滑道上的位置,通过控制滑程而达到不同的试验速度。滑道倾角可调范围为5°~75°,最大承载质量250 kg。可控制滑坡体入水速度为0.2~2.5 m/s。
在涌浪产生过程的观测中,采用高速摄影仪拍摄滑坡入水产生涌浪的整个过程,拍摄速度为0.1 s/张。在滑动方向上布置若干监测点,采用电容式波高仪记录不同位置涌浪高度随时间的变化过程;在河道适当断面设置高程背景板作为辅助记录,背景板的网格分辨率为5 mm。
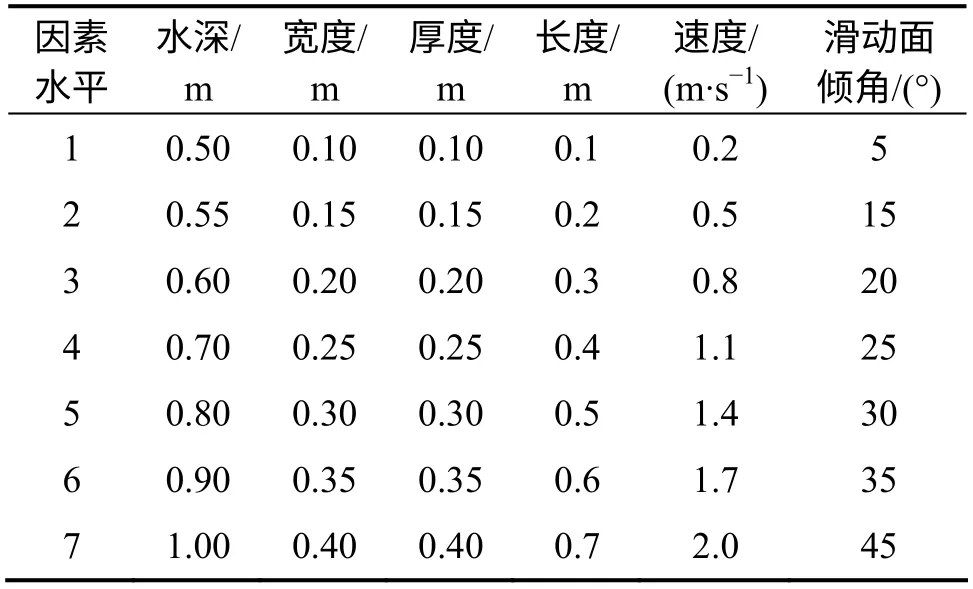
表1 各因素的水平值Table 1 Levels of each factor
2 冲击涌浪特征
冲击涌浪是具有一定速度和体积的滑体冲击水体形成涌浪的一个过程。从滑坡涌浪的发生位置来看,冲击涌浪的范围包括滑坡下滑点处的浪溅区和以产生首浪为起始的近源区[5]。远源区属于波浪传播区,不属于本文冲击涌浪概念的范畴。
从试验观测来看,整个冲击涌浪产生的过程如图1 所示。滑体以一定速度入水,首先在水体表面形成一层斜向上运动的薄层舌状水波,即水舌(t=0.1 s),当滑体不断的下滑进入水体,更多的水体形成水舌(t=0.2 s)并向前运移至最高点(t=0.34 s);同时,水体不断被滑体侵占,在水舌尾部被侵占处形成一个空腔(t=0.48 s);空腔周围水体在内外水压差及重力作用下快速汇入空腔内,并相互撞击在空腔中央涌起巨大的水花(t=0.62 s);水花再次落入空腔(t=0.73 s),并将空腔内水体向四周挤压,形成可以向远处传播的实体涌浪(t=1.28 s)。
一般冲击涌浪的第1 波实体波浪称为首浪,首浪涌至最高处时离水面的高度称为首浪高度。在涉水滑坡涌浪中,首浪波峰的幅度最大[10]。在首浪形成后,波浪逐渐向四周传播且浪高逐渐衰减。
图1 中的滑体速度v=1.5 m/s,长度、宽度和厚度分别为0.40,0.25 和0.25 m,滑动面倾角为35°,滑体密度ρ=2.2 g/cm3。
在整个过程中,有2 次可向前传播的水体雍高形成,即水舌和首浪,它们都属于冲击涌浪,即冲击涌浪为发生在近源区以内的水舌和首浪的合称。

图1 冲击涌浪产生过程中不同时刻的水体形态Fig.1 Characteristic of water shape during formation of impulse wave
3 试验结果分析
3.1 冲击涌浪中的水舌
滑坡前缘以一定的速度撞击水面,将部分能量传递给局部水体,接受能量的水体同时受到后面整个水域的阻力,在极短时间内,还来不及向前传播,这种前推后阻的作用迫使水体向斜上方运动,形成了可以向前传播的水舌。当水舌运移至一定距离和高度后在重力作用下破碎并溅落于水面或对岸岸坡。从水舌产生至消失,整个过程历时很短,但通过高速摄像仪可以清楚的观察其形态特征。水舌形成后其运动至最高点的高度(即水舌高度)和最高点离“舌根”的距离(即水舌长度)具有一定的规律性,而且水舌的运动轨迹与以上2 个参数密切相关,其数据可以通过背景幕读出。将水舌高度和水舌长度作为水舌形态的2 个特征量,通过这2 个量来确定水舌运动特征。
3.1.1 水舌最大高度
从水舌的形成原因来看,只有滑坡下滑速度足够大,才会在瞬间形成水舌,缓慢入水的滑坡不会形成水舌;滑体撞击水体时的迎水面积越大,接受能量的水体的范围越大,形成水舌雍高的水体越多;滑坡入水的角度不同,水舌向上传播的方向也不同,因此,水舌形态与滑坡速度,迎水面积,滑坡倾角有较大相关性。
通过测量系统读取每一组刚性正交试验中水舌的最大高度,在SPSS 软件中对试验数据进行正交分析,寻找水舌高度与滑坡的长度、宽度、厚度、下滑速度、水深及岸坡坡角这6 个因素的影响关系,结果如表2所示。
从表2 可知6 个因素对水舌高度的敏感性从大到小依次为速度、水深、滑动面倾角、厚度、宽度、长度。
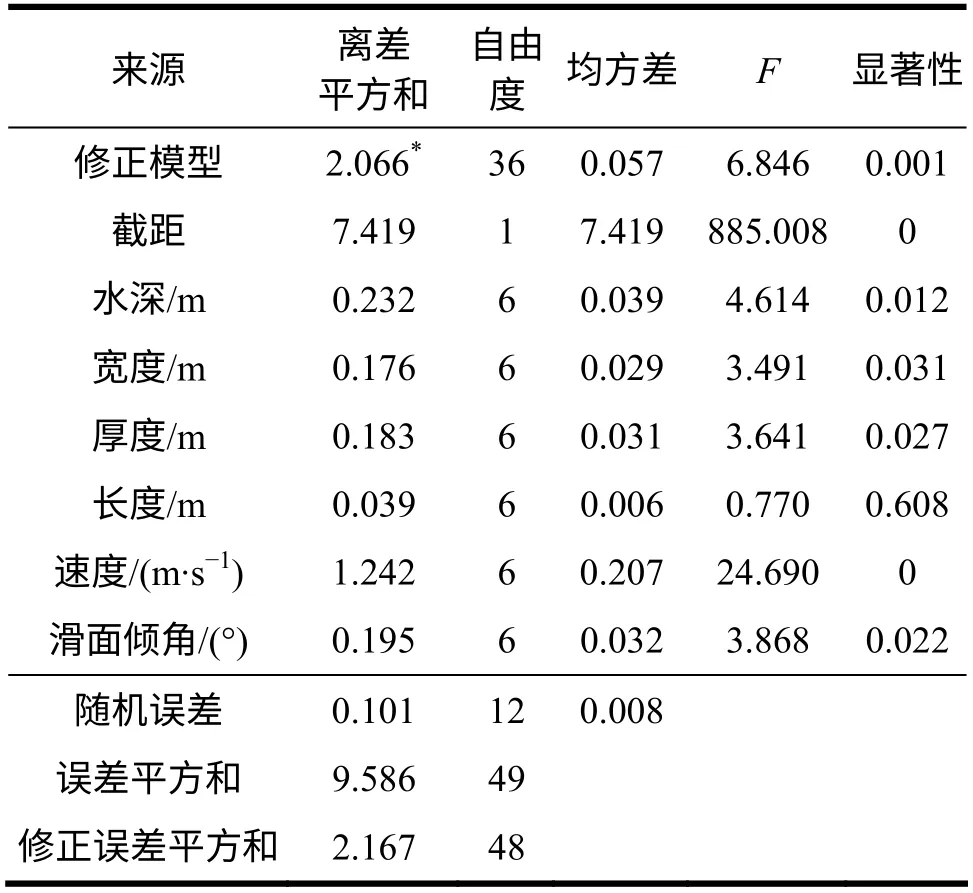
表2 方差分析结果Table 2 Results of variance analysis
查表得:f0.1(6,12)=2.9,f0.05(6,12)=4,f0.01(6,12)=7.72,因此,有: F速速>f0.01(6,12);f0.01(6,12)> F水水>f0.05(6,12);f0.05(6,12)> F倾倾> F厚速> F宽速>f0.1(6,12);f0.1(6,12)> F长速。
由此可知,速度为高显著性因素,水深为显著性因素,厚度、宽度和倾角次之,长度为非显著性因素。Fritz 等[3]提出“弗劳德数越大,越容易在坡肩处形成波峰;弗劳德数较小,水体变形不会在坡肩处出现尖陡的波峰”,本次分析结果与该观点相一致。
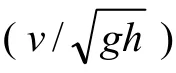

其中:η′为水舌高度,m;v 为滑坡速度,m/s;w 为宽度,m;t 为厚度,m;h 为水深,m;a 为滑动面倾角,(°)。
实验值与预测值的相关系数R 为0.79,说明预测值与实验值达到了较好的拟合。试验值与回归预测值对比如图2 所示。
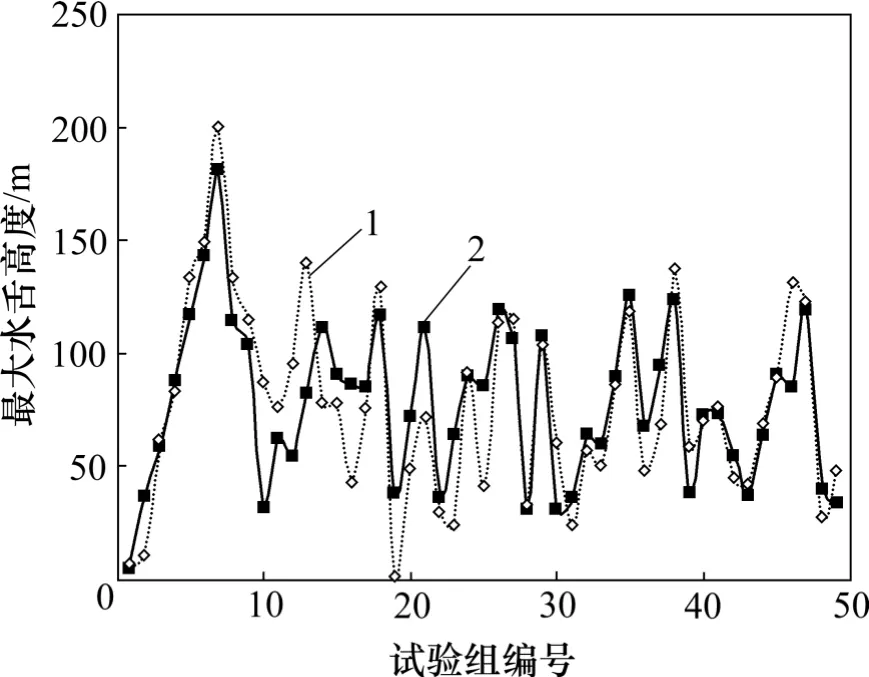
图2 试验值与预测值对比图Fig.2 Experiment data and prediction data of water tongue height
3.1.2 水舌长度预测
分别读取每一组试验中的水舌长度,同样利用方差分析方法分析水舌长度与各影响因素之间的显著性关系,得到6 个影响因素中对水舌长度的影响显著性依次为:F 厚速> F速速> F倾倾> F宽速> F长速> F水水,其中厚度、速度和倾角为3 个显著影响因素。水舌长度与水舌高度也存在较强的相关性,在SPSS 软件中将水舌长度与速度的水平分量(vcoαs)、水舌高度(η′)和滑坡厚度(t)进行多元线性回归分析,得到水舌长度公式为

预测值与试验值的相关系数R 为0.82,说明该公式可以较好地预测水舌长度。
3.1.3 运动轨迹
水舌空中运动时,其水平方向受空气阻力作用,垂直方向受重力和空气阻力作用。当水舌运动上升至碎波点后,水舌在重力作用下破碎成水花并成散体状下落。在水舌形状分散破碎之前,空气阻力对水体作用相对重力作用可以忽略不计。从其受力条件来看,运动轨迹可以用抛物线方程来表示。不考虑空气阻力作用,以滑坡入水点为原点,水舌在空中的运动方程式为
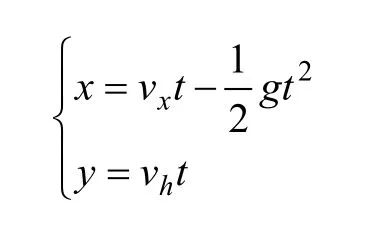
其中:vx和vh分别为水舌初始速度在水平和垂直方向的分量。水舌运动轨道示意图如图3 所示。
从多组试验观测结果来看,水舌往往运动至越过最高点后的一段距离便开始解体,其轨迹后半部分不能构成完整的抛物线。根据观测,水舌运动至约3s/2距离后开始解体,部分水舌继续向前运动,部分在重力作用下垂直下落。此时所携带的能量随之迅速减小,致灾能力也迅速降低。
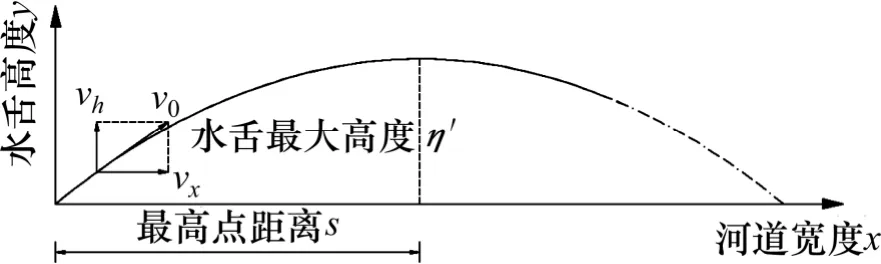
图3 水舌运动轨迹示意图Fig.3 Profile of water tongue motion curve
根据水舌高度与水舌长度的位置关系得到抛物线的轨迹图,其表达式为:
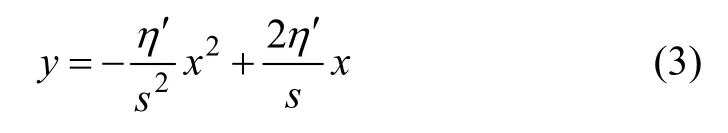
其中:x 为河道宽度,适用范围为x<2s;y 为水舌高度。根据式(1)~(3)可以计算水舌拍打至对岸的高度。当河道宽度x>2s,水舌的运动和解体均位于河面上,此时水舌不能运动至对岸。
3.2 冲击涌浪中的首浪
首浪是波浪向远处传播的开始,也是波浪能量衰减的开始。国内外已有许多学者对首浪进行了试验研究并提出了不同条件下的经验公式。表3 所示为国内外几种典型滑坡涌浪计算公式。其中:Hmax为首浪高度,h 为河道最大水深,v 为滑坡最大入水速度,α 为滑面倾角,l 为滑坡入水长度,t 为滑坡平均宽度,w为滑坡平均厚度,b 为河道宽度。
本文图4 中的“首浪计算高度”为利用文献[9]中提出的首浪公式计算的高度。该公式适用于三峡库区比较宽广的河道上的滑坡涌浪计算。
3.3 水舌与首浪的关系
从涌浪产生的过程来看,最大水舌高度的可辨识度均远大于实体首浪。水舌高度和首浪高度散点图如图4 所示。可见,约有85%的点位于y=4x 和y=16x这2 条直线之间,表明水舌高度为首浪高度的4~16 倍。

表3 国内外一些典型的涌浪公式Table 3 Some landslide wave equations at home and abroad

图4 水舌高度和首浪高度散点图Fig.4 Scatter diagram of water tongue and initial water wave

由图5 可以看出:在本试验的设计方案上,当弗劳德数F<0.1 时,首浪高度与计算高度均较小,而水舌高度仍然较高;随着F 的增加,计算高度与水舌高度数量级较一致,在结果上更接近,且远高于首浪高度;水舌高度和计算高度均呈明显的波动上升趋势,而首浪增加不明显。
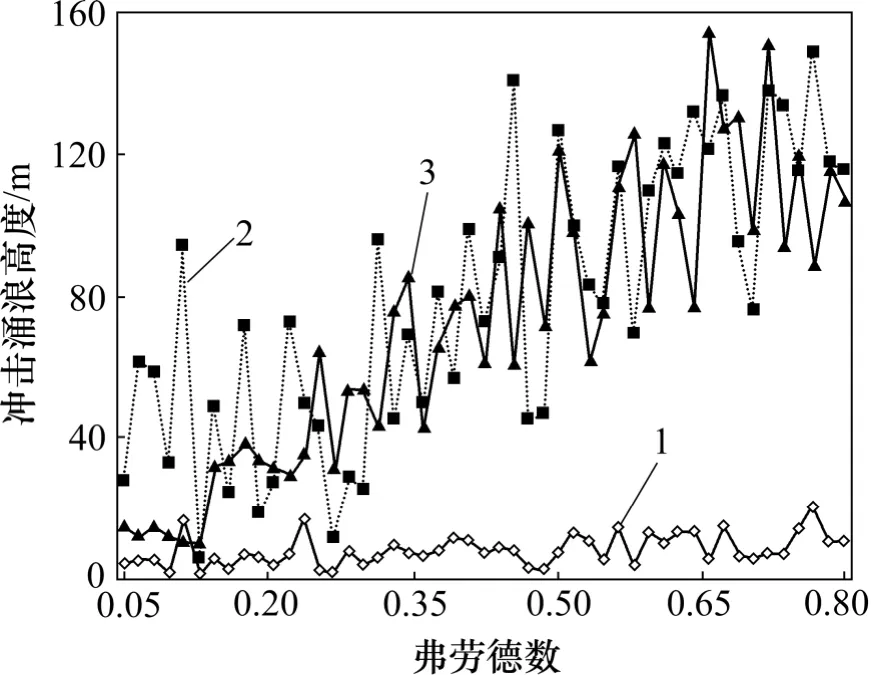
图5 冲击涌浪高度随弗劳德数F 的变化曲线Fig.5 Variation of impulse wave height with Froude number
由试验方案可知,由于受试验条件的限制,试验中的滑体宽度较小,经相似比(1:200)还原至原型后的宽度仍然比三峡库区的滑坡宽度约小1 个数量级。将本试验方案中的滑体规模和速度按相似比还原后,再将宽度放大10 倍,使滑体规模与实际滑坡接近。再次用文中推导的冲击涌浪计算公式与文献[7]中的公式对比,按弗劳德数排列,结果如图6 所示。
由图6 可知:3 种涌浪高度均随着F 的增加呈波动上升趋势,且水舌高度>计算高度>首浪高度。经统计,三峡库区的大多数滑坡的弗劳德数均属于本试验范围内[12],因此,基于本试验的水舌和首浪公式均适用于三峡库区的滑坡涌浪计算,而潘家铮公式[7]计算高度较首浪偏大,较水舌偏小,在使用时需考虑其适用条件。
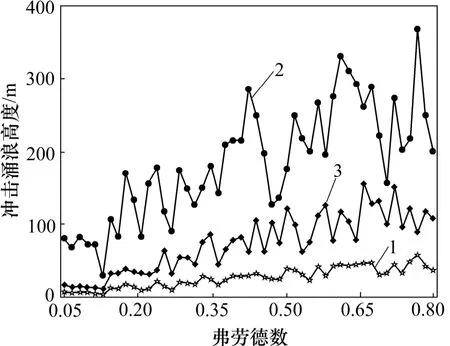
图6 冲击涌浪计算高度随弗劳德数F 的变化曲线Fig.6 Variation of calculated impulse wave height with Froude number
4 实例分析
4.1 清江水布垭库区大堰塘滑坡
大堰塘滑坡位于湖北清江水布垭库区左岸斜,2007-06-15 在水位上升和暴雨的联合作用下,大堰塘滑坡发生大规模塌滑,入江体积达300×104m3。滑坡对岸涌浪爬高为50 m 左右,下游20.8 km 水布垭大坝处涌浪爬坡仍高4 m 左右,涌浪波及到3 个乡镇,造成滑坡上游险区1 km 以外的对岸邻近乡镇1 人死亡、3 人下落不明,下游5 km 以外3 人去向不明的严重后果[13]。
滑坡平面形态呈簸箕形,后缘高程约为620 m,前缘高程约为225 m,坡度为35°~40°。南北纵长约600 m,前缘最宽处达900 m,平均宽约500 m,滑体平均厚度为10 m,面积约为30×104m2,体积约为300×104m3(图7 和图8)。
根据滑坡的平剖面形态特征,选取滑体形状计算参数及速度如表4 所示。
用基于本试验提出的水舌和首浪经验公式分别计算冲击涌浪高度,并计算横断面传播浪[9]和爬坡浪[8,14]。利用表3 中的Fritz 公式[2-3]和潘家铮公式[7]对该滑坡涌浪进行对比分析计算,结果见表5。
从计算结果来看,最大水舌高度>潘家铮公式[7]计算高度>本文公式首浪高度。Fritz 公式[2-3]计算的结果远小于前两者,原因是该公式适用于弗劳德数F∈[1,4.8][3]的范围,在本实例中F 小于此范围,因此计算结果偏小。计算结果显示:冲击涌浪中的首浪高39.6 m,传播至对岸造成的爬坡浪高为49.6 m;最大水舌高105.9 m,水舌长度s 为158 m,河道宽度200>3s/2,此时拍打至对岸的水舌高度为47.9 m,虽然与爬坡浪高较接近,但此时水舌已经开始解体,携带的能量远不如爬坡浪高,因此对岸最高点的涌浪的痕迹主要由爬坡浪作用形成。该计算结果与观测到的高度基本一致,验证首浪高度计算的正确性,也说明了潘家铮公式计算结果偏高。
4.2 秭归千将坪滑坡
2003-07-13 T 0:20,湖北省秭归县沙镇溪镇千将坪村二组和四组山体突然下滑,造成房屋倒塌、厂房摧毁、交通中断、青干河堵塞,同时掀起大于20 m 高的巨浪,打翻船舶22 艘,经济损失惨重。千将坪滑坡位于青干河北岸岸坡,滑坡宽度410~480 m;滑坡最大长度自后缘三角滑壁至青干河南岸滑坡堆积体为1 205 m;滑坡平面面积0.52 km2,滑坡厚度:中后部20~30 m,中前部40~50 m,最大厚度59 m,滑坡体积为1 542 万m3。高程140~210 m 为10°左右缓坡平台,210~380 m 为20°左右斜坡,380~400 m 为10°左右缓坡平台,400 m 以上为30°斜坡,岸坡西侧及前沿西部为高25~40 m 的临空陡崖,岸坡前沿东部为15°左右的缓坡,岸坡前沿河滩高程约100 m。滑坡滑动后,滑舌跨过青干河,呈散体堆积在青干河及其南岸,滑舌最大爬高约80 m[15]。
根据滑坡的平剖面形态特征,选取滑体形状计算参数及速度[16]如表6 所示。
滑坡涌浪计算方法同实例1,结果见表7。

表4 滑体计算参数取值Table 4 Calculation coefficients of landslide
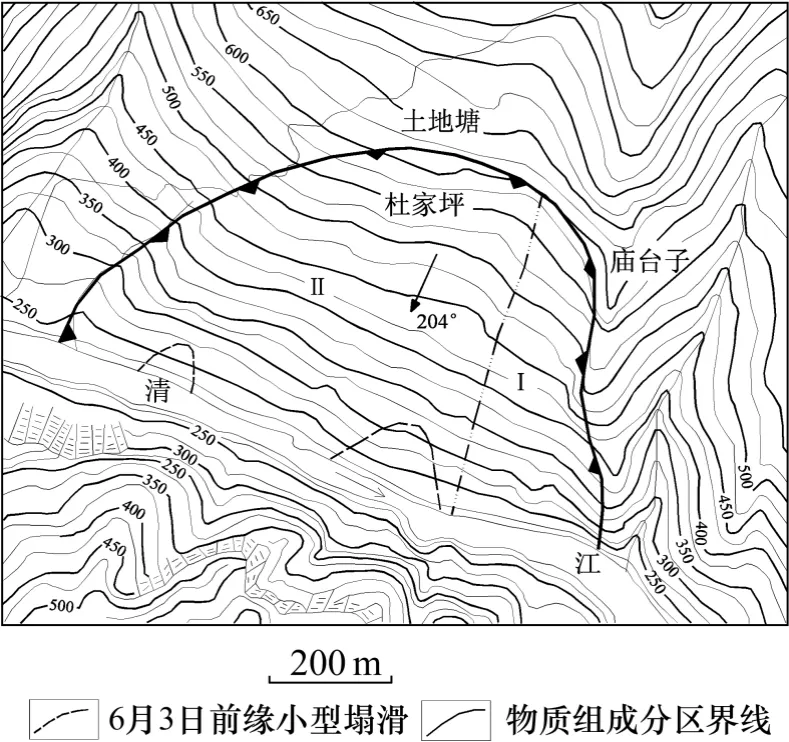
图7 大堰塘滑坡平面图Fig.7 Plan view of Dayantang landslide

图8 大堰塘滑坡河道剖面图Fig.8 Profile of Dayantang landslide

表5 大堰塘滑坡冲击涌浪计算结果Table 5 Impulse wave height of Dayantang landslide
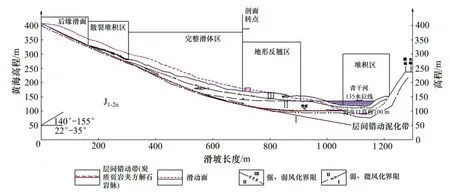
图9 千将坪滑坡纵剖面分区示意图Fig.9 Profile of Qian Jiangping landslide

表6 滑体计算参数取值Table 6 Calculation coefficients of landslide

表7 千将坪滑坡冲击涌浪计算结果Table 7 Impulse wave height of Qianjiangping landslide
从计算结果来看, 最大水舌高度>潘家铮公式[7]计算高度>本文公式首浪高度。Fritz 公式[2-3]计算结果偏小,其原因与实例1 相同。由此说明Fritz 公式[2-3]并不适用于文中实例类型的滑坡初始涌浪计算。本例中的最大水舌高度为127.9 m,水舌长度为221.2 m,略大于河道宽度,说明水舌还未达到最高点就已经怕打至对岸,拍打至对岸的高度为126.9 m,此时水舌的能量最高,且远高于爬坡浪高度,其拍打作用对影响范围内的承载体是一个重大的威胁。
综上所述,在计算滑坡涌浪时应辨别经验公式的适用范围,正确选择合适的计算公式;分析库岸滑坡的冲击涌浪时,需综合考虑水舌和首浪的作用。
5 结论
(1) 基于滑坡涌浪物理模拟试验,将冲击涌浪的概念定义为滑坡涌浪产生过程中发生在近源区以内的水舌和首浪的合称。水舌主要是受滑体冲击水体形成,其携带部分能量,运移一段距离后在重力作用下破碎并溅落于水面或对岸岸坡;首浪是携带大部分能量的实体波浪,可以向远处不断传播并对滑坡发生点河道上下游产生一定的破坏作用。
(2) 将水舌最大高度η′和水舌长度s 作为定义水舌的2 个特征量。针对水舌最大高度进行正交分析可知,滑坡速度为高显著性因素,水深为显著性因素,宽度、厚度和倾角次之,长度为非显著性因素。基于逻辑线性回归分析得到了水舌最大高度与各影响因素的相关关系式。
(3) 水舌长度的影响显著性依次为: F厚速> F速速> F倾倾> F宽速> F长速> F水水,其中厚度、速度和倾角为3 个显著影响因素。基于线性回归分析得到了水舌长度与各影响因素的关系式。
(4) 根据水舌空中运动的受力情况,将抛物线型作为其运动轨迹方程,用最大水舌高度和水舌长度定量水舌运动轨迹,可计算任意河道宽度时水舌运动至对岸的高度。
(5) 试验得到水舌高度为首浪高度的4~16 倍。对于三峡库区的滑坡,潘家铮公式计算高度较首浪偏大,较水舌偏小,在使用时需考虑其适用条件。
(6) 选取已经发生滑动的清江大堰塘滑坡和秭归千将坪滑坡为例,分别计算其首浪高度,爬坡浪高及水舌拍打至对岸的涌浪高度,计算结果均与实际观测结果较一致,验证了冲击涌浪中水舌和首浪公式的可靠性以及二者之间关系的正确性。
(7) 本物理试验针对三峡库区滑坡涌浪而设计,经验公式适用于三峡库区以及与三峡库区环境类似的库岸滑坡,本研究为实际应用中滑坡涌浪的调查和涌浪高度的计算提供较好的理论基础,为山区库岸滑坡涌浪预警工作提供了重要的技术支持。
致谢:本研究受到中国地质调查局项目(121201122017)的资金支持,特此感谢!
[1] Slingerland R, Voight B. Evaluating hazard of landslide-induced water waves[J]. Journal of the Waterway Port Coastal and Ocean Division, 1982, 108(4): 504-512.
[2] Fritz H M. Initial phase of landslide generated impulse waves[D].Zurich: Swiss Federal Institute of Technology, 2002.
[3] Fritz H M, Hager W H, Minor H E. Near field characteristics of landslide generated impulse waves[J]. Journal of Waterway, Port,Coastal, and Ocean Engineering, 2004, 130(6): 287-302.
[4] van der Meer J W. Wave run-up and wave overtopping at dikes[R]. Netherlands. Technical Advisory Committee on Flood Defence, 2002: 43.
[5] Walder J S, Watts P, Sorensen O E, et al. Tsunami generated by subaerial mass flows[J]. Journal of Geophysical Research, 2003,108(B5): 2236-2254.
[6] Ataie-Ashtiani B, Nik-Khah A. Impulsive waves caused by subaerial landslides[J]. Journal of the Environ Fluid Mech, 2008,8(7): 263-280.
[7] 潘家铮. 建筑物的抗滑稳定与滑坡分析[M]. 北京: 水利出版社, 1980: 133-151.PAN Jiazheng. Structure stability against sliding and landslide analyze[M]. Beijing: China Hydraulic Press, 1980: 133-151.
[8] 汪洋. 水库库岸滑坡速度及其涌浪灾害研究[D]. 武汉: 中国地质大学工程学院, 2005: 84-85.WANG Yang. The research on speed of the landslide and its surge hazard in reservoir[D]. Wuhan: China University of Geosciences. Faculty of Engineering, 2005: 84-85.
[9] 殷坤龙, 刘艺梁, 汪洋, 等. 三峡水库库岸滑坡涌浪物理模型试验研究[J]. 地球科学: 中国地质大学学报, 2012, 37(5):1067-1074.YIN Kunlong, LIU Yiliang, WANG Yang, et al. Research on physical model experiments of landslide-induced surge in Three Gorges Reservoir[J]. Earth Science: Journal of China University of Geosciences, 2012, 37(5): 1067-1074.
[10] Zweifel A, Hager W H, Minor H E. Plane impulse waves in reservoirs[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2006, 132(2): 358-368.
[11] Kamphuis J W, Bowering R J. Impulse waves generated by landslides[J]. Coastal Engineering Proceedings, 1970, 1(12):575-588.
[12] 殷坤龙, 汪洋, 吴益平, 等. 三峡库区三期地质灾害防治监测预警工程专业监测崩塌滑坡灾害点涌浪分析与危害评估[R].武汉: 中国地质大学(武汉)工程学院, 2008.YIN Kunlong, WANG Yang, WU Yiping, et al. Landslides generated wave analyze and hazard evalution in the Third period of Three Gorges Reservoir geo-hazard prevention and monitoring project[R]. Wuhan: China University of Geosciences(Wuhan). Faculty of Engineering, 2008.
[13] 殷坤龙, 杜娟, 汪洋. 清江水布垭库区大堰塘滑坡涌浪分析[J]. 岩土力学, 2008, 29(12): 3266-3270.YIN Kunlong, DU Juan, WANG Yang. Analysis of surge triggered by Dayantang landslide in Shuibuya reservoir of Qingjiang river[J]. Rock and Soil Mechanics, 2008, 29(12):3266-3270.
[14] 汪洋, 殷坤龙. 水库库岸滑坡涌浪的传播与爬高研究[J]. 岩土力学, 2008, 29(4): 1031-1034.WANG Yang, YIN Kunlong. Research on propagation and climb height of surge triggered by landslide in reservoir[J]. Rock and Mechanics, 2008, 29(4): 1031-1034.
[15] 邬爱清, 丁秀丽, 李会中, 等. 非连续变形分析方法模拟千将坪滑坡启动与滑坡全过程[J]. 岩石力学与工程学报, 2006,25(7): 1297-1303.WU Aiqing, DING Xiuli, LI Huizhong, et al. Numerical simulation of startup and whole failure process of Qianjiangping landslide using discontinuous deformation analysis method[J].Chinese Journal of Rock Mechanics and Engineering, 2006,25(7): 1297-1303.
[16] 肖诗荣, 刘德富, 胡志宇. 三峡库区千将坪滑坡高速滑动机制研究[J]. 岩土力学, 2010, 31(11): 3531-3536.XIAO Shirong, LIU Defu, HU Zhiyu. Study of high speed slide mechanism of Qianjiangping landslide in Three Gorges Reservoir area[J]. Rock and Mechanics, 2010, 31(11):3531-3536.
