隔热结构对塞块式量热计热流测量的影响

2014-03-30杨庆涛白菡尘

实验流体力学 2014年5期

杨庆涛,白菡尘,张涛,王辉

(1.中国空气动力研究与发展中心超高速所高超声速冲压发动机技术重点实验室,四川绵阳 621000; 2.中国空气动力研究与发展中心超高速所,四川绵阳 621000)

0 引言

高超声速飞行器及其发动机在大气层内飞行(工作)时，结构承受很大的热载荷，在防热/冷却结构设计时，必须清楚地掌握结构壁面的热环境，热流测量是掌握壁面热环境的常用手段[1]。

热流测量技术常用一维传热的假设，通过测量元件温度梯度或随时间的变化，计算得到表面的热流。对于沿壁面法向传递的热流传感器，如水卡量热计、塞块式量热计和零点量热计等，为了使传感器测量元件的实际传热过程接近理论假定，需要使传感器与其安装基体有效隔热，以忽略两者之间的侧向传热。

为实现传感器与基体之间有效隔热，通常通过空气隙与隔热材料两种方式。在空气隙宽度较小，且其中没有气流流动的条件下，可以忽略空气对流换热的影响。空气是一种理想的隔热材料，将两者的导热换热量降低到最低。然而，如果空气隙开口在气动加热面，在空气隙开口附近由于外流的冲击产生涡流，从而产生附加侧向加热[2]。另外，如果传感器与基体之间存在较大温差，则两者之间的辐射换热量将不能忽略。

使用隔热材料进行隔热时不必考虑辐射换热的影响。不同隔热材料对传感器测量准确度的影响各不相同，可以通过试验筛选出最佳隔热材料，或者利用理论修正侧向传热的影响。在试验方面，文献[2]对比了使用不同隔热材料时热流传感器测量结果的不同，文献[3]对等离子体流中不同间隙结构对测量的影响进行了试验研究。

在理论修正方面，文献[4]建立了如下隔热层传热修正模型：

(1)

其中：ΔT为塞块式量热计与周围材料温差，简单地假定试验期间周围材料温度不变，通过塞块的温升得到；Kloss通过标定给出。

文献[5]认为侧向传热热流主要取决于塞块平均温度与支架(基体)之间的温差以及隔热材料的热阻，并推导得到了基于试验曲线的修正公式。文献[6]则通过用停止试验后的降温速率来估算量热塞的散热量。

然而，如果隔热材料也承受高温气流加热，那么隔热材料表面温度也会迅速上升，并且会远高于传感器及其周围基体的温度。隔热材料与传感器之间的温差会产生附加热流。本文利用理论和数值仿真，分析隔热层温升对塞块式量热计测量的影响，并探讨隔热结构优化的途径。

1 量热计隔热结构传热分析与改进

1.1传热分析

考虑图1所示的塞块式量热计，纯铜圆柱量热塞(高度l、直径d1)侧向利用隔热材料与圆柱模型基体(内径d2=2R2)隔开，传感器、隔热层与基体表面平齐，并承受相同状态(气流恢复温度Tr、对流换热系数h)的气动加热。

利用热电偶测量可测得量热塞底部温度变化。理想情况下，量热塞只受到表面的气动加热，在线性响应段，量热塞底部温升率(利用热电偶测量)等于量热塞平均温升率，正比于入射热流[1]：

(2)

图1 常见塞式量热计结构

由于量热塞、隔热层和基体温度不同，三者之间会存在侧向传热，造成测量误差：

(3)

其中：q1为量热塞与隔热层交界面上的侧向(径向)热流；qm为测得热流。

因此，侧向传热的测量误差：

(4)

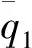
可见，q0一定时，侧向传热误差与量热塞长径比(即侧向和感应面面积比)有关。如果侧向传热条件一定，选择长径比较小的量热计有利于减小侧向传热误差。

高温气动加热气流在隔热层表面流过，由于隔热层导热率要远小于量热塞和基体，因此其表面附近温度会远高于后两者，而其他区域温度会明显低于量热塞温度。这种明显的温差会导致隔热层与量热塞之间复杂的换热。

(1) 量热塞向隔热层的导热

在线性响应段，量热塞各处温升率接近(理想情况下相等)。为便于分析，当热量在隔热层内的扩散深度小于其厚度时，将量热塞向隔热层的传热近似为一维半无限大传热问题，有：

(5)

其中，ρ2、cp,2、k2分别为隔热材料的密度、比热容和导热率；负号表示量热塞散热。

在测量中，将测得的底面温度温升率近似为量热塞侧面温升率，代入式(5)，可以利用式(4)对测量结果进行修正：

(6)

(2) 隔热层表面温升的影响

隔热层材料导热率要远低于量热塞，在气动加热条件接近的情况下，隔热层的表面及附近温度会远大于量热塞，使隔热层向量热塞传热，造成量热计的测量误差。

另一方面，在外部气流温度较高时，隔热层表面温度有可能超过材料使用温度，使隔热层产生烧损，在量热塞周围产生凹坑，改变局部的气动热环境，造成局部气动热环境模拟的偏差。显然，隔热层材料导热率越低，表面温度过高造成的烧损越明显。避免表面烧损要求材料导热率高，与减小量热塞散热损失的要求矛盾。

1.2结构改进

根据上述分析，不仅隔热层向量热塞传热的区域是侧向传热测量误差的重要来源，并且有可能由于烧损造成局部外形改变，造成模拟条件变化。

隔热层结构优化的基本思路是减小气动热环境对隔热层的直接加热，从而减小隔热层向量热塞的传热，同时避免隔热层表面的高温损坏。在隔热层与量热塞之间接触热阻可忽略时，量热塞向隔热层的传热损失利用式(6)进行修正。

为避免高温气流烧损隔热层，在隔热层上设计一层金属，将高温气流与隔热层隔开；为减小金属层向量热塞的传热，减小金属层与量热塞的接触面积；为避免高温气流将该金属层烧损，将金属层与外壳(基体)的接触面增大并且整体成型，将热量导入基体中。由此设计了如图2所示的隔热层结构，尖楔与量热塞的接触面很小(<0.2mm)，接近于线接触，并且通过机械装配实现过渡配合，希望利用接触热阻减小两者之间换热。

图2 改进的隔热结构

2 数值分析模型

为对上述传热分析和优化设计进行验证分析，建立了轴对称有限元瞬态传热模型。量热塞和基体材料为纯铜，隔热层材料选择硅质岩水泥，基本尺寸如表1所示。隔热层上方的尖楔(夹角45°)材料设为水泥时，隔热结构与图1相同，设为纯铜时与图2相同。计算时的网格如图3所示。

数值分析的基本假定和边界条件如下：

(1) 假定材料为常物性；

(2) 忽略量热塞、隔热层与基体其他表面换热(绝热条件)；

(3) 尖楔设为纯铜时，忽略与基体的接触热阻(模拟整体成型条件)；

表1 数值计算量热计尺寸

图3 网格划分

(4) 量热塞和基体表面为气动加热条件(Tt=5000℃,h=1500W/(m2·K)，冷壁热流约7.5MW/m2)，其中气流温度选取了电弧加热气流的一个典型温度状态；

(5) 计算时间0.5s。

3 计算结果与分析

3.1常见隔热结构

(1) 温度分布与侧向导热误差

图4为常见隔热结构(见图1)模型在0.5s时的温度分布。可见其与理论分析一致，隔热层可以分为两个区域：在距离表面较近的区域内，隔热层温度远高于量热塞温度，使隔热层向量热塞传热，这一因素使测量值偏高；而其他区域隔热层温度上升缓慢，低于量热塞温度，量热塞向隔热层传热，使测量值偏低。对于计算条件，隔热层的高温放热区域高度<1.5mm(见图5)。

图4 常见结构温度分布(0.5s)

图5 侧向传热热流分布

图6为相对误差项E随时间的变化。在初始时刻，隔热层材料的导热率要远小于量热塞，其表面附近温度迅速上升，远快于量热塞温度上升，因此向量热塞的传热迅速增大，造成误差项不断上升。随着时间推移，量热塞与隔热层低温区域之间的温差不断增大，造成量热塞损失热量增加，尽管总体上仍是量热塞获得额外的热量造成测量偏高，但热损失份额不断提高，造成在特定时刻(此时相对误差最大)后，相对误差不断缩小。

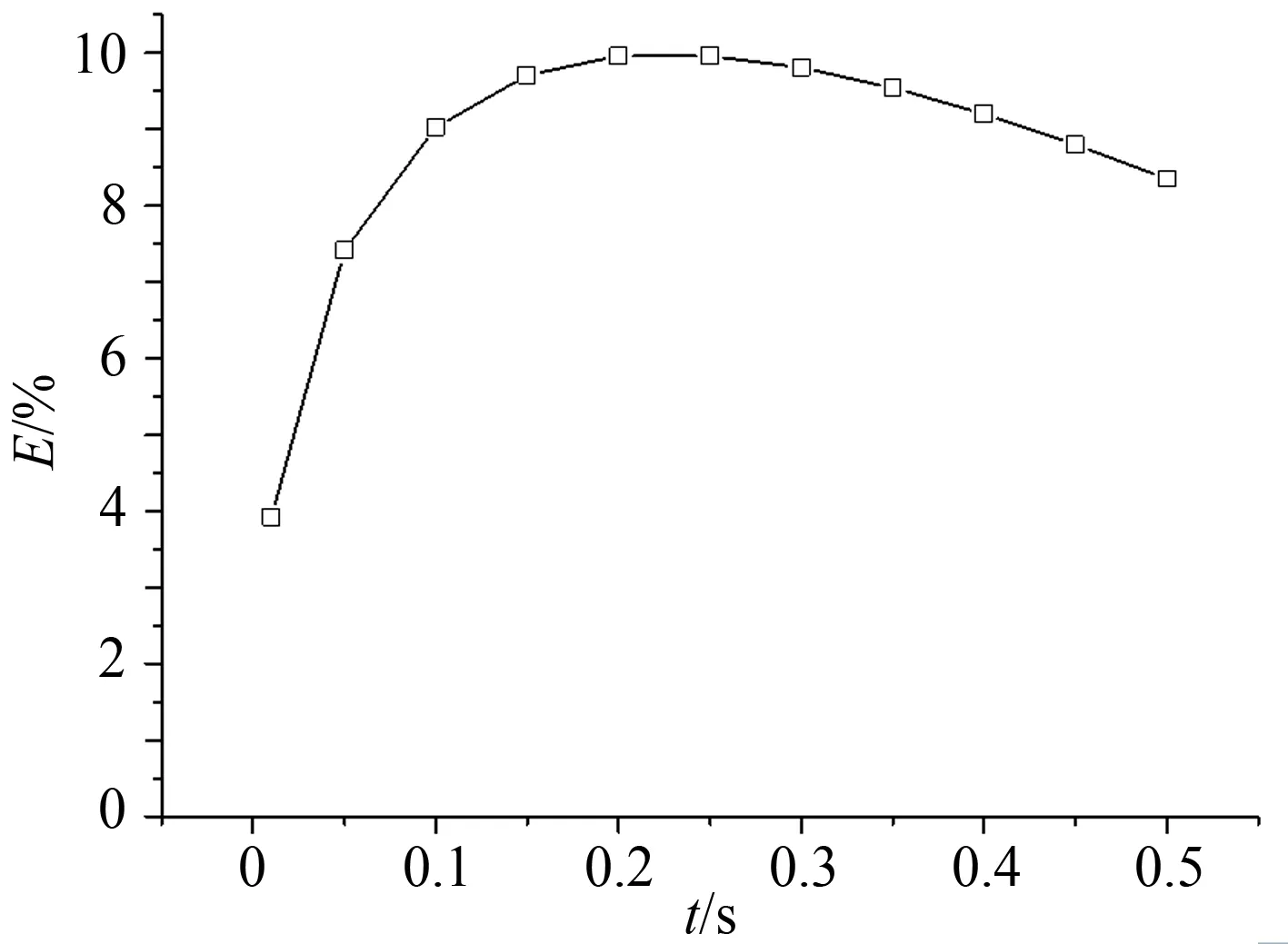
图6 相对误差随时间的变化

对于计算条件，隔热层表面的最高温度超过2000℃，已经超过大部分常见耐温隔热材料的使用温度(见图7)。

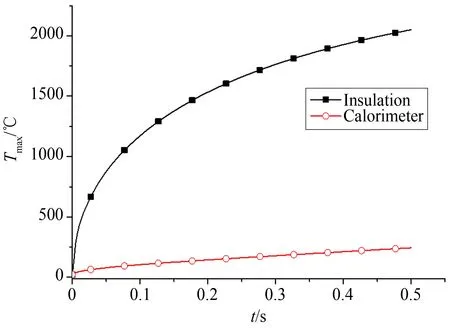
图7 量热塞与隔热层最高温度

可见，如果隔热结构直接接触高温气流表面，不但有可能发生烧损，而且向量热塞的传热也会对量热计的测量结果产生重要影响。

(2) 铜-隔热材料接触热阻的影响

由于不同材料的交界面存在接触热阻，两种材料在界面上的温度并不相同[8]，因此只有在可以忽略接触热阻时，才能用金属的界面温度作为隔热层界面温度处理。

根据文献[9]，铜与隔热层的接触热阻与隔热层的形态有关，成型材料与铜的接触热阻比颗粒状材料要低1个数量级。在研究铜-隔热材料接触热阻对测热的影响时，将尖楔材料与铜壁面的接触热阻分别设为0、1×10-4和1×10-3m2·K/W，不考虑隔热层表面气动加热的影响(表面无气动加热)。

上述3种情况下，0.5s量热塞的侧向传热热流如图8所示。可见量热塞侧向散热量在接近表面的区域最大，在底部最小。接触热阻对量热塞的热损失有明显影响，R=0(即忽略接触热阻)时，量热塞最大散热量为5.3×105W/m2；R=1×10-4m2·K/W时，最大散热量为4.0×105W/m2；R=1×10-3m2·K/W时，最大散热量为1.4×105W/m2。

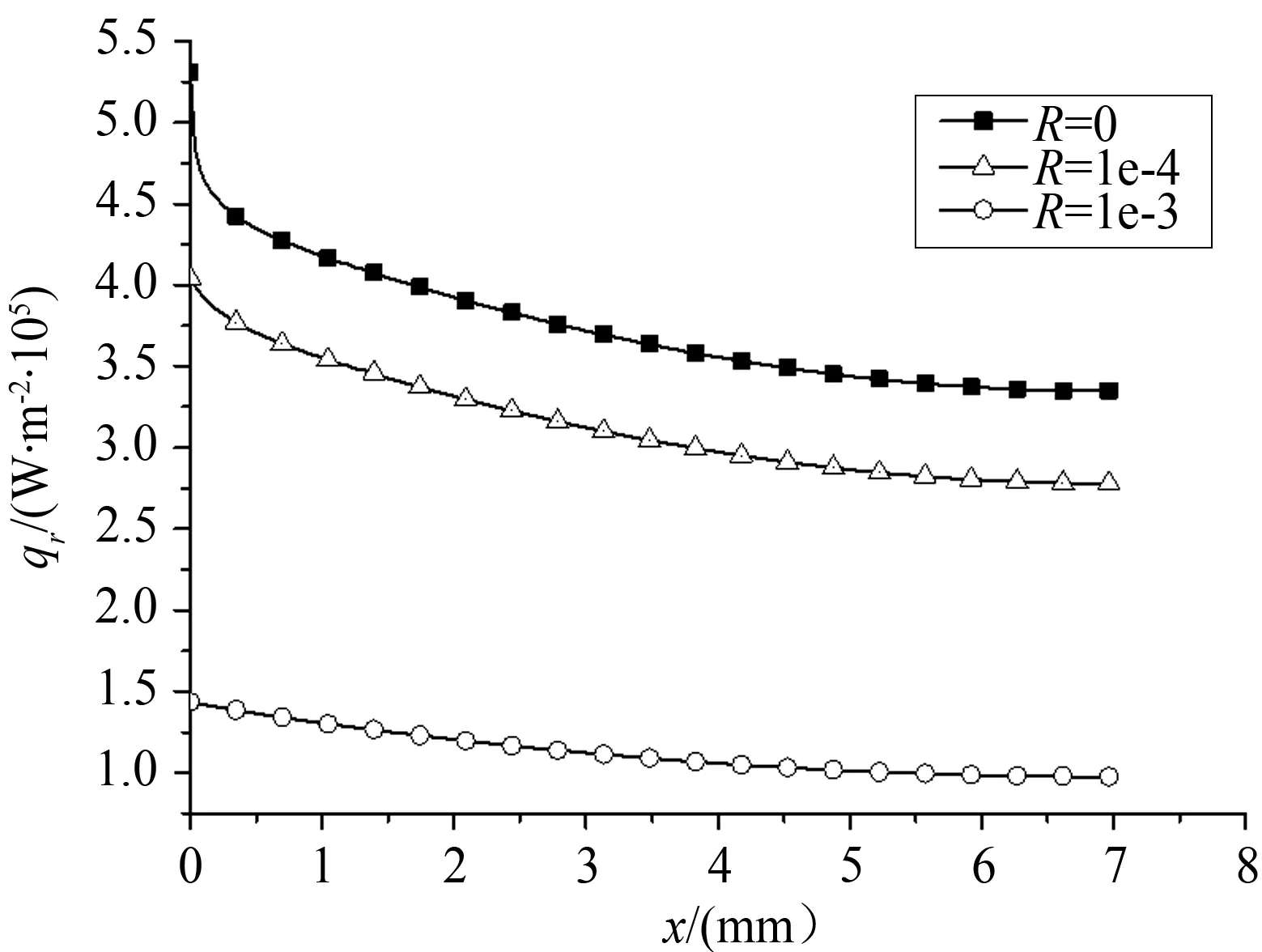
图8 接触热阻对侧向传热的影响

(3) 数据处理的效果与适用性

图9为不同接触热阻时，利用式(2)和式(6)计算热流的热流测量误差。利用式(2)计算热流时，由于未能考虑散热的影响，测量热流均偏低(见图9(a))。在接触热阻较大时，由于散热损失被明显抑制，利用式(2)计算得到的相对误差较小，R=1×10-3m2·K/W时，线性响应段的最大误差不大于-9％。如果接触热阻较小，散热损失较大，R=1×10-4m2·K/W时，线性响应段的相对误差随着时间增大，最大在0.5s时超过了-20％，与忽略接触热阻的结果接近。

利用式(6)获得的修正热流忽略了量热塞与隔热材料接触热阻，并且假定量热塞各处温度等于底部温度(实际上底部温度低于量热塞平均温度)。由于接触热阻的存在减少了量热塞的热损失，使量热塞底部温度高于忽略接触热阻的情况。因此考虑接触热阻的修正热流比完全忽略时要高(见图9(b))。接触热阻较大(R=1×10-3m2·K/W)时，修正后的热流明显偏高，最大偏差超过了20％。接触热阻较小(R=1×10-4m2·K/W)时，接触热阻相对于隔热材料自身热阻是小量，获得了较好的修正效果，线性响应段的修正热流相对偏差与忽略接触热阻的情况接近，小于1.5％。忽略接触热阻的线性段修正偏差不大于-10％，偏差主要来源于量热塞各处温度等于底部温度的假定。

在实际测量中，隔热材料与量热塞之间的接触热阻跟材料特性及安装工艺有关。如果两者的接触热阻较大，宜采用式(2)处理测量数据；如果接触热阻较小，宜采用式(6)处理。由于接触热阻实际上难以测定，因此对于具体的量热计结构，应对量热计进行标定，选择合适的处理方法。

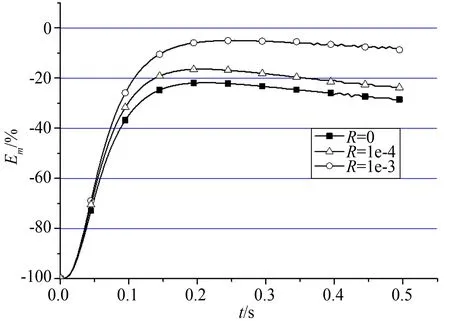
(a) 式(2)

(b) 式(6)

3.2改进隔热结构

根据文献[9]，在一定温度范围内，铜-铜表面接触热阻的大小与接触面压力有关，压力越小，接触热阻越大。尖楔在基体上直接加工成型，尖楔与量热塞的接触压力可以通过加工尺寸来改变，因此接触热阻可以根据需要控制在一定范围内。

计算中，设定楔形尖与量热塞之间接触热阻分别为1×10-4和4×10-4m2·K/W[9]。铜-隔热层接触热阻设为1×10-4m2·K/W。

尖楔接触热阻为1×10-4m2·K/W，楔尖高度为0.2mm时的温度分布如图10所示。可见整个量热计结构的最高温度不大于300℃，起到了保护隔热层材料的预期目的。

图11为尖楔高度为0.2mm、隔热材料不同尖楔接触热阻情况下的测量误差。可见在计算条件下，尽管存在尖楔向量热塞的导热(见图12)，但由于尖楔与量热塞接触面积很小(约占总面积的2.9％)，对量热塞侧向总换热量的贡献较小，所以不同接触热阻时的测量误差接近。与上节相似，利用式(2)得到的线性段偏差接近20％，利用式(6)得到的线性段偏差不大于10％。可见，尖楔结构不但可以保护隔热层不被烧损，而且尖楔对测量的影响较小，可以采用前述的修正方法处理数据。

图10 改进结构温度分布

图11 不同尖楔热阻的热流测量误差

图12 尖楔结构侧向传热

4 结论

根据上述分析，可得以下主要结论：

(2)在处理数据时应考虑量热塞与隔热结构接触热阻的影响，算例条件下接触热阻较大时侧向换热误差小于10％；

(3) 基于半无限大体假定的热损失修正方法可以用于量热塞与隔热材料接触热阻可忽略时的数据处理，算例条件下可将侧向误差降低到10％以内；

(4) 尖楔结构可以保护隔热层不被烧损，而且对测量影响较小，可以用所研究的处理方法计算热流。

参考文献:

[1]刘初平.气动热与热防护试验热流测量[M].北京:国防工业出版社,2013.

Liu Chuping.Heat flux measurement in aerothermal and thermal protection tests[M].Beijing: National Defense Industry Press,2013.

[2]涂建强,刘德英,陈海群.长时间隔热材料环境的稳态热流测量方法[J].宇航材料工艺,2008,(2): 76-80.

Tu Jianqiang,Liu Deying,Chen Haiqun.Steady-state heat-flux measurement method for environment of long-time insulation materials[J].Aerospace Materials & Technology,2008,(2): 76-80.

[3]Nawaz A,Gorbunov S,Terrazas-Salinas I and et al.Investigation of slug calorimeter gap influence for plasma stream characterization[C].43rdAIAA Thermophysics Conference,New Orleans,Louisiana,2012.

[4]Childs P R N,Greenwood J R,Long C A.Heat flux measurement techniques[J].Pro Instn Mech Engrs,1999,213 part C: 655-677.

[5]Nawaz A,Santos J.Assessing calorimeter evaluation methods in convective and radiative heat flux environment[C]//10th AIAA/ASME Joint Thermophysics and Heat Transfer Conference,Chicago,Illinois,2010.

[6]ASTM E 457-96,Standard test method for measuring heat-transfer rate using a thermal capacitance (slug) calorimeter[S].

[7]张志成,潘梅林,刘初平,等.高超声速气动热与热防护[M].北京: 国防工业出版社,2003.

Zhang Zhicheng,Pan Meilin,Liu Chuping,et al.Hypersonic aerothermodynamics and thermal protection[M].Beijing: National Defense Industry Press,2003.

[8]Incropera F P,DeWitt D P,Bergman T L,et al.传热和传质基本原理[M].葛新石,叶宏译.北京: 化学工业出版社,2009.

Incropera F P,DeWitt D P,Bergman T L,et al.Fundamentals of heat and mass transfer[M].Translated by Ge X S,Ye H.Beijing: Chemical Industry Press,2009.

[9]王国庆,朱东生,林琳.吸附剂之间及其与铜表面之间的传热强化研究[J].化学工程,1999,27(6): 13-15.

Wang Guoqing,Zhu Dongsheng,Lin Lin.Heat transfer enhancement between adsorbents and between adsorbent and copper surface[J].Chemical Engineering (China),1999,27(6): 13-15.

[10]彭小方,石零,王建,等.低温下Cu-Cu固体间界面热阻的激光光热法研究[J].低温与特气,2006,24(5): 34-37.

Peng Xiaofang,Shi Ling,Wang Jian,et al.Experimental research on the thermal contact resistance by photothermal measurement between Cu-Cu in low temperature[J].Low Temperature and Specialty Gases,2006,24(5): 34-37.

作者简介: