基于等效介电常数的激光雾中衰减研究

魏海亮，邵利民，王宁宁

(1．海军大连舰艇学院研究生管理大队，辽宁 大连116018;2．海军大连舰艇学院军事海洋系，辽宁 大连116018;3．91040部队，山东 青岛266321)

1 引言

海雾是指海洋与大气相互作用特定条件下出现在海上或沿海地区上空低层大气的一种凝结现象，是悬浮于大气边界层中大量水滴或冰晶使得水平能见度小于1 km的危险性天气现象［1］。激光在海雾中传输时要受到折射、透射、散射和吸收等作用，其中散射和吸收是引起激光衰减的主要原因。由于激光的波长与雾滴的尺度相当，因此海雾对激光的衰减值得关注。目前国内外已经建立了许多用于计算激光大气透过率的大型数据库和计算包，比较典型的如LOWTRAN7［2］、MODTRAN［3］等，但其分辨率较低，计算适用范围有限，计算较为繁琐;基于能见度的经验雾衰减计算模型在工程中应用广泛［4］，但模型仅考虑能见度和激光波长，没有更多考虑雾的其他物理特征;基于Mie散射理论的衰减计算模型考虑了雾的滴谱分布等因素［5－6］，由于是以单次散射为基础，当雾能见度较小时该模型就不再适用。

海雾的电磁性质是基于传输激光波长、环境温度等参数的非线性函数，很难从理论上直接给出它们与介电常数的确切函数表达式。研究随机介质介电常数的一般做法是在特定温度下采用测量方法得到经验公式，如已经取得的雨滴、冰、雪和沙尘等介电常数的经验公式，这些方法反映了随机介质中粒子的介电特性，对研究激光的传输效应有重要作用，但不能充分反映随机介质整体的介电特性，不能体现介质物理特性对等效介电特性的影响。本文根据电介质极化理论推导出了雾滴粒子的等效介电常数的一般计算模型，并进一步得出传输衰减的计算公式。

2 改进的等效介电常数模型

海雾发生时，实际是雾滴粒子按照一定的谱分布弥散在空气中，形成一种宏观近似均匀的随机介质。假设雾滴的等效介电常数为εeff，则雾区中的电位移矢量为［7］:

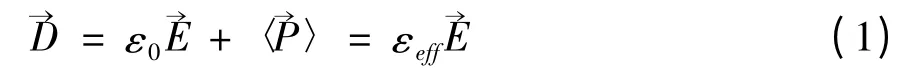
其中，εw代表雾滴粒子的介电常数，即水的介电常数。

利用上式计算雾滴粒子的等效介电常数最大的局限就是静场假设，因此为了计算激光条件下的等效介电常数，可用下式粒子极化率代替［9］:

其中，f为激光频率;fr为雾滴粒子的共振频率。

以平流雾经验雾滴谱模型为例，仿真、计算了雾区的等效介电常数，水的介电常数用双Debye公式计算，雾滴半径取0．01～36μm，温度为10℃。图1为雾区等效介电常数仿真和计算结果。

图1 雾区等效介电常数虚部

从图1中可以看出海雾介质的等效介电常数是频率和能见度的非线性函数;同时当能见度变化时雾滴谱分布也随之不同，因此海雾的雾滴尺寸及滴谱分布对雾介质等效介电常数也有一定的影响;而温度对等效介电常数的影响则体现在其对水的介电常数的作用上，不过温度对雾滴粒子的电磁传输特性影响相对较小［9］。

利用等效介电常数计算激光雾中传输特征衰减(衰减率)的公式为［10］:

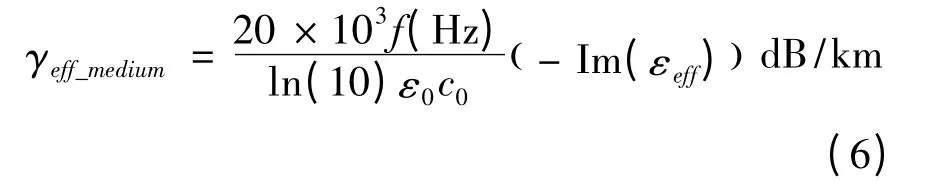
式中，c0为真空光速。

3 仿真与讨论

3．1 海雾的雾滴谱特征

雾滴谱是雾中不同大小雾滴数密度的分布，是表征雾结构的一个重要特征参量。被广泛使用的雾滴谱模型是Khragian－Mazin分布模型，利用含水量与能见度的关系可以得到经验平流雾滴谱分布如下:

其中，V为能见度;r为雾滴半径。从式(7)中可以看出，改变能见度的大小就可以获得不同的雾滴谱分布。

由于不同气象条件下海雾过程都有其各自特点，因此雾滴谱的研究也多是个例研究，下面是分别根据舟山地区和沪宁地区两次海雾过程实测数据拟合得出的雾滴谱分布［11－12］:

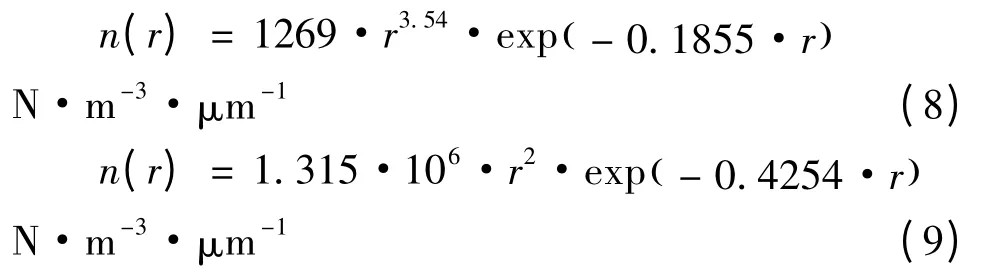
图2为海雾的滴谱分布，其中图2(a)为不同能见度情况下平流雾经验雾滴谱分布，随着海雾能见度的降低，雾滴谱宽度变宽，雾滴数浓度峰值也随之向大雾滴方向变化;图2(b)为当V=0．5 km时，平流雾经验雾滴谱分布与两个海雾个例雾滴谱分布的比较，由图中的雾滴谱分布可见，经验雾滴谱和沪宁地区海雾个例的雾滴谱较窄，主要表现为r＜15μm的小雾滴;而舟山地区海雾个例的雾滴谱则相对较宽，大的雾滴明显增多，雾滴数浓度峰值在r=20μm附近。

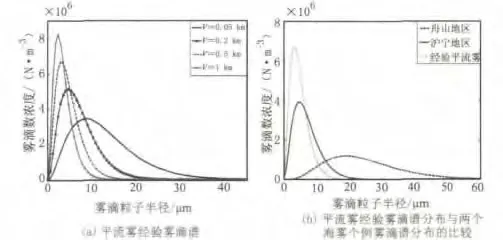
图2 雾的滴谱分布

3．2 激光雾中传输衰减仿真

在工程应用中，激光雾中传输衰减计算通常采用经验衰减模型如Kim模型、Naboulsi模型等［4］。图3(a)、(b)分别以0．63μm和10．6μm波长为例，对等效介电常数衰减模型与经验衰减模型的仿真比较，其中雾滴谱采用平流雾经验雾滴谱模型。从图中可以看出，各模型中激光雾区衰减率随能见度变化趋势相同。当激光波长为0．63μm时，两经验模型计算结果基本重合;在V＞2 km情况下激光波长不管是0．63μm还是10．6μm，等效介电常数衰减模型与经验模型预测结果都差别不大，随着能见度的降低特别是能见度低于1 km时各模型计算的衰减率差别变大。这是因为经验模型在计算时仅考虑了海雾的能见度因素，而能见度是海雾的宏观物理特征，当能见度很低时雾滴粒子多散射效应对衰减率的影响不容忽视。式(4)是根据电介质极化理论导出了海雾发生时雾滴粒子的等效介电常数的一般计算模型，在推导过程中考虑了雾滴粒子的平均退极化场和单个粒子的退极化场分别对粒子外部场和粒子内部场的影响，考虑了雾滴粒子物理特性对等效介电常数的影响。相比经验模型，物理机理和概念清晰，能够反映海雾物理特征对等效介电特性的影响，能够方便地计算具有不同物理特征雾滴粒子的等效介电特性。

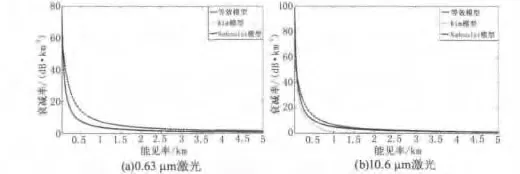
图3 激光雾区衰减率随能见度的变化曲线

从图4(a)、(b)显示了不同雾滴谱分布对激光衰减率的影响，其中图4(a)采用平流雾经验雾滴谱，不同能见度情况下雾滴谱分布变化很大，如图2(a)所示;图4(b)中平流雾经验雾滴谱中V=0．5 km，各雾滴谱分布的差异从图2(b)中可以看出。从图中可以看出雾滴谱分布对激光衰减率的大小影响非常明显，各雾滴谱分布的衰减率差别很大，体现了激光衰减对海雾环境物理特征的依赖。

图4 不同雾滴谱分布对激光衰减率的影响

4 结束语

海雾是一种具有吸收或者散射特性的传输介质，研究激光在海雾中传输的衰减特性，对于了解海雾的光电遮蔽性能具有重要意义。根据电介质极化理论推导出了激光雾区传输的等效介电常数衰减计算模型，在推导过程中考虑了雾滴粒子的平均退极化场和单个粒子的退极化场分别对粒子外部场和粒子内部场的影响，并充分考虑了海雾环境本身的物理特征对激光衰减特性的影响。本文建立的模型物理机理和概念清晰，提供了一种计算激光雾中衰减的新方法。由于相关的海雾衰减数据稀缺，本文的研究工作局限于理论分析，今后可结合实测数据对模型进一步验证。

［1］ XU Xiaofeng，GU Jianfeng，LI Yongping．Marine meteorological disasters［M］．Beijing:Meteorological Press，2009:102－104．(in Chinese)许小峰，顾建峰，李永平．海洋气象灾害［M］．北京:气象出版社，2009:102－104．

［2］ F Filbet，G Russo．High order numerical methods for the space non－homogeneous boltzmann equation［J］．Comput Physics，2003，186:457－480．

［3］ LIU Weicaho，QI Linlin，HE Hongrang，et al．Numerical study on atmospheric transmission of 1．06μm laser［J］．Laser＆Infrared，2011，41(5):520－524．(in Chinese)刘伟超，齐琳琳，何宏让，等．1．06μm激光大气透过率特性的数值计算研究［J］．激光与红外，2011，41(5):520－524．

［4］ LI Di，CHEN Hui．Study on attenuation characteristic of laser propagation in rain and fog［J］．Electronic Design Engineering，2011，19(9):1－5．(in Chinese)李娣，陈辉．激光大气传输的雨雾衰减特性研究［J］．电子设计工程，2011，19(9):1－5．

［5］ LI Xuebin，GONG Chunwen，LI Chao，et al．Size distribution and attenuation for infrared radiation of fog particles［J］．Laser＆Infrared，2009，39(7):743－745．(in Chinese)李学彬，宫纯文，李超等．雾滴谱分布和雾对红外的衰减［J］．激光与红外，2009，39(7):743－745．

［6］ KE Xizheng，MA Dongdong，LIU Jiani．Study attenuation of laser transmission in fog［J］．The Journal of Light Scattering，2009，21(2):104－109．(in Chinese)柯熙政，马冬冬，刘佳妮．激光在雾中传输的衰减研究［J］．光散射学报，2009，21(2):104－109．

［7］ PENG Weicai，CHEN Kanghua．Calculation of effective electromagnetic parameters in random mixture media of magnetic iron fiber［J］．Rare Metal Materials and Engineering，2005，34(9):1047－1410．(in Chinese)彭伟才，陈康华．磁性纤维随机混合媒质等效电磁参数的计算［J］．稀有金属材料与工程，2005，34(9):1047－1410．

［8］ P Lorrain，D Corson．Electromagnetic fields and waves［M］．Beijing:People's Education Press，1980:62－87．(in Chinese)P劳兰，D R考森．电磁场与电磁波［M］．北京:人民教育出版社，1980:62－87．

［9］ ZHOU Xingli，XIE Yanan，YANG Zhengde．Effect study of clouds and fogdrops on microwave transmission characteristics［J］．Meteorological Science and Technology，2011，39(5):661－665．(in Chinese)周星里，谢亚楠，杨正得．云雾对电磁传输特性影响的研究［J］．气象科技，2011，39(5):661－665．

［10］M Z Gao，T SYeo，P SKooi，et al．Rain attenuation calculation using dielectric mixture with deformed rain drops［C］．Geoscience and Remote Sensing Symposium，IGARSS'93．Better Understanding of Earth Environment．，International，1993:1250－1252．［11］YANG Zhongqiu，XU Shaozu，GENG Biao．Formation and microphysical structure features of spring sea fog in Zhoushan region［J］．Acta Oceanologica Sinica，1989，11(4):431－438．(in Chinese)杨中秋，许绍祖，耿骠．舟山地区春季海雾的形成和微物理结构［J］．海洋学报，1989，11(4):431－438．

［12］HUANG Jianping，MEI Qingyin，JIN Yongcai．Microphysical structure features and evolution processes of radiation fog in Huning region［J］．Meteorological Monthly，1998，24(5):3－7．(in Chinese)黄建平，梅清银，靳永才．沪宁地区辐射雾的微物理结构及其演变［J］．气象，1998，24(5):3－7．