基于受力分析的制动鼓耦合分析

袁汇江

（潍坊科技学院汽车工程学院，山东寿光262700）

0 引言

制动系统是汽车上最重要的安全装置之一。在鼓式制动器中，制动力靠摩擦片和制动鼓之间的摩擦产生，由于制动蹄上的摩擦片对制动鼓内表面存在较大的推力，使制动鼓内表面承受挤压应力，同时在鼓壁截面上还将承受张应力［1］。

汽车行车制动时，汽车由高速降至低速或停车，使得汽车的动能转化为热能。理论研究表明，在制动停车期间产生的热能大部分被制动鼓吸收，使制动鼓的工作面积聚了大量的热能，其工作表面温度随着制动的持续而升高，使工作表面产生较大的热应力［2］。

本研究主要通过对制动鼓进行热分析、结构分析和热应力耦合场分析，从而分析结构和热应力分别对制动鼓的影响，为进一步研究和优化制动鼓的设计参数提供理论依据。其中的计算是在大型通用有限元分析软件ANSYS中完成的。

1 制动鼓的力学分析

制动器是凸轮促动的领从蹄式［3］，其主要设计参数如表1所示。

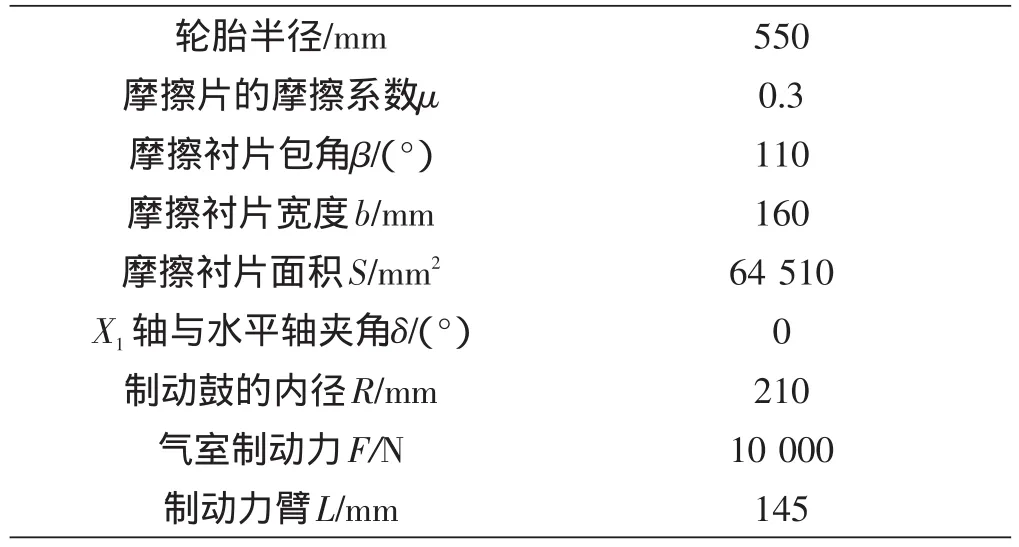
表1 制动器的主要设计参数

1.1 制动鼓所受的机械载荷

制动鼓与制动蹄之间的压力沿摩擦衬片长度的分布符合正弦曲线规律。在摩擦衬片表面取一横向微元面积［4］，制动力矩示意图如图1所示。它位于a角内，面积为bRda。

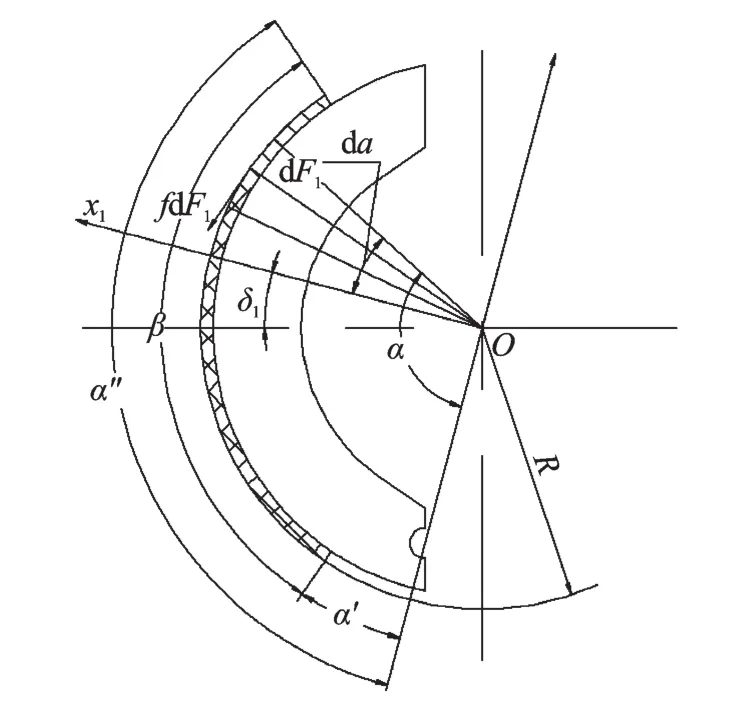
图1 制动力矩示意图

由鼓作用在微元面积上的法向力为：

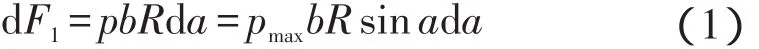
摩擦力dF1产生的制动力矩为：

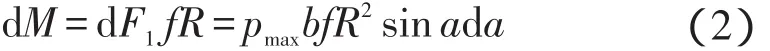
从a'到a''区段积分式（2）可得：

式中：pmax—制动鼓工作表面受到的压力。

则：

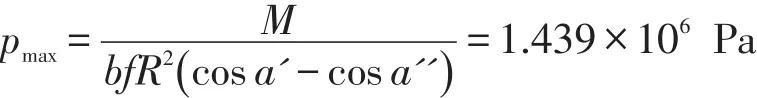
1.2 简化模型

由于制动鼓的结构和受力情况比较复杂，笔者在建立力学模型时作以下假设［5］：

（1）在制动过程中摩擦片的摩擦系数不随温度和压力变化而变化；

（2）制动气室的压力保持不变；

（3）摩擦片和制动鼓之间在包角范围内完全接触；

（4）摩擦衬片只发生径向变形，且符合虎克定理；

（5）制动蹄与制动鼓之间的最大压力Pmax均匀地作用在制动鼓的工作表面。

2 制动鼓的耦合分析

2.1 有限元建模与材料特性

本研究通过Pro/E三维绘图软件建立制动鼓的实体模型，其分布质量与实际一致，实体模型如图2所示。本研究将Pro/E三维模型导入ANSYS中，对制动鼓的实体模型划分网格，建立有限元模型，有限元模型如图3所示。

图2 制动鼓实体模型

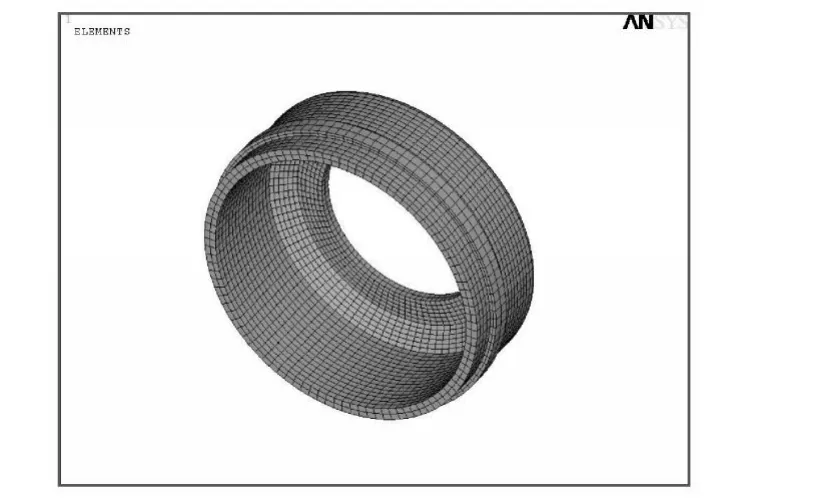
图3 制动鼓有限元模型

制动鼓的材料采用HT250，其材料属性如表2所示。

表2 HT250材料属性

2.2 单元选择及网格划分

根据热分析、结构分析和耦合分析的需要，建模时必须选择热单元和结构单元分别进行网格划分［6-7］。热分析采用Solid70单元，结构分析采用Solid45号单元。这两种单元在热分析与结构分析中可以满足顺序耦合的要求相互转换。网格的划分采用扫掠式网格划分，划分后的制动鼓有限元模型如图2所示。

2.3 边界条件及荷载

热分析的边界条件［8］：取制动鼓的换热系数为62.3 W/m2℃，假设大气的温度为20℃，分析制动蹄与制动鼓接触的内表面在150℃的温度载荷下的温度分布，对流载荷施加在制动蹄与制动鼓接触的表面上。热分析边界条件及荷载如图4所示。

图4 热分析的边界条件

结构分析的边界条件：在施加边界条件时，制动鼓的车轮螺栓孔采用刚性约束，即设置X、Y、Z方向位移为0。当制动蹄片与制动鼓内表面接触时，产生的摩擦力为：f=μ×Pmax×S=27 849.6 N，同时制动鼓表面受到的作用力为：Pmax=1.439×106Pa。

耦合分析边界条件：利用顺序耦合方式，将热分析得到的节点温度作为体载荷，同时施加机械载荷，约束方式与结构分析相同。耦合分析的边界条件与荷载如图5所示。

图5 耦合分析的边界条件

2.4 计算结果

以下分析有关计算结果［9-11］。

2.4.1 热分析

当制动鼓与制动蹄的摩擦片制动时产生了大量的热量，制动鼓会发生热膨胀效应。通过制动鼓的热分析，得出的制动鼓在150℃温度载荷作用下的位移分布图如图6所示，应力分布图如图7所示。从制动鼓位移分布图可以看出，制动鼓的最大位移发生在制动鼓的外侧部位（位移分布图中的深色区域），约为0.38 mm。从制动鼓热应力分布图可以看出，制动鼓的危险部位发生在制动鼓外侧（应力分布图中的深色区域）及制动鼓内壁与制动蹄摩擦片的接触区域（应力分布图中的浅色区域），其应力值大约为180 MPa。

图6 制动鼓位移分布图

图7 制动鼓热应力分布图

2.4.2 结构分析

当不考虑制动鼓的热效应，只考虑制动蹄作用在制动鼓内壁上的外张压力和摩擦力时，得出的制动鼓的位移分布图如图8所示，应力分布图如图9所示。计算结果表明，不考虑制动鼓的热效应前提下，制动鼓的最大位移发生在制动鼓的外侧部位（位移分布图中的深色区域），约为0.297 mm。从制动鼓的应力分布图可以看出，制动鼓的危险部位发生在制动鼓内壁与制动蹄摩擦片的接触区域（应力分布图中的浅色区域）。

2.4.3 耦合分析

图8 制动鼓位移分布图

图9 制动鼓等效应力分布图

本研究在结构分析中读入热分析结果文件，其他载荷和边界条件的施加和结构分析相同。笔者利用等效应力反映制动鼓的表面最大压力和摩擦力及温度载荷共同作用下的应力场，制动鼓的位移分布图和等效应力分布图如图10、图11所示。

图10 制动鼓位移分布图

图11 制动鼓等效应力分布图

制动鼓的最大变形位移发生在制动鼓外侧边缘部位（位移分布图中的深色区域），约为0.4 mm。从制动鼓应力分布图可以看出，制动鼓的危险部位也发生在制动鼓外侧（应力分布图中的深色区域）及制动鼓内壁与制动蹄摩擦片的接触区域（应力分布图中的浅色区域），其应力值大约为197 MPa。计算结果表明：耦合分析所得位移约为结构分析中的1.34倍，说明温度对制动鼓的变形影响很大；与结构分析相比，耦合分析所得的应力较大，说明温度对制动鼓的强度有较大影响；在机械载荷和热载荷共同作用下，制动鼓的最大应力没有超过其材料的强度极限，满足制动鼓的强度要求。

3 结束语

（1）通过热分析、结构分析及耦合分析可知，制动鼓的危险部位发生在制动鼓外侧及制动鼓内壁与制动蹄摩擦片的接触区域，这为实际工作过程中，制动鼓失效多发生在该部位附近提供了理论依据。

（2）耦合分析所得位移约为结构分析中的1.34倍，说明温度对制动鼓的变形影响较大；与结构分析相比，耦合分析所得的应力较大，说明温度对制动鼓的强度有较大影响；在机械载荷和热载荷共同作用下，制动鼓的最大应力没有超过其材料的强度极限，满足制动鼓的强度要求。

（3）以上计算是基于大气温度20℃，制动蹄摩擦片与制动鼓接触内表面的温度载荷为150℃的初始条件，在其他初始条件下，分析结果会有所不同，但对制动鼓的变形及热应力的影响趋势应一致。

（

）：

［1］陈家瑞.汽车构造［M］.北京：机械工业出版社，2011.

［2］方明霞，冯奇.制动鼓的有限元分析［J］.上海汽车，1994（4）：4-8.

［3］鲁道夫.汽车制动系统的分析与设计［M］.北京：机械工业出版社，1985.

［4］包陈，吴志俊.ANSYS工程分析进阶实例［M］.北京：中国水利水电出版社，2006.

［5］梁建术，赵明洁.工程力学［M］.北京：电子工业出版社，2012.

［6］张胜兰，郑冬黎，郝琪，等.基于HyperWorkshop的结构优化设计技术［M］.北京：机械工业出版社，2013.

［7］王钰栋，金磊，洪清泉.HyperMesh＆HyperView应用技巧与高级实例［M］.北京：机械工业出版社，2013.

［8］袁春静，吴永根，葛振亮.制动鼓瞬态温度场有限元分析［J］.科学技术与工程，2006（6）：4-8.

［9］欧贺国，方献军，洪清泉.RADIOSS理论基础与工程应用［M］.北京：机械工业出版社，2013.

［10］TAUCHERT T R.Thermal shock of orthotropic rectancular plat es［J］.Thermal Stresses，1989，12（3）：241-258.

［11］CHANG J S，WANG J H，TSAI T Z.Thermally induced vibration of thin laminated plat es by finit e element method［J］.Computers&Structures，1992，42（1）：117-128.