基于VB的优化双圆弧拟合误差分析及其算法改进

张 弛， 陈锦昌， 申艺杰

（1.华南理工大学设计学院，广东 广州 510006；2.华南理工大学机械与汽车工程学院，广东 广州 510640）

在数控加工中，刀具的路径一般为直线和圆弧，所以大多数数控机床只能实现直线插补和圆弧插补。在加工带有曲线轮廓的工件时，按照刀具的路径特点，需要把曲线转化为由直线或圆弧组成的样条以方便刀具的加工。进行直线插补时由于刀具在每个插补段都要经历加速、匀速、减速和停顿，使加工时间延长且产生过多的振动和磨损，而使用圆弧插补能实现匀速加工且加工曲线光滑还能减少加工时间提高效率，因此，使用圆弧逼近来代替曲线更为有利[1-2]。圆弧逼近一般分为单圆弧逼近和双圆弧逼近。单圆弧逼近具有使用圆弧数少连续性好等优点，但同时稳定性差、缺乏灵活性，不能处理有拐点的情况；双圆弧逼近则具有较高的灵活性和稳定性，更加适用于曲线轮廓工件的数控加工[3]。

本文主要研究双圆弧对曲线的逼近及其优化设计，运用VB编程实现了曲线轮廓工件的双圆弧拟合以及拟合误差的分析计算，使用随机数和判断函数实现了简单的双圆弧拟合优化设计，求出可行的拟合参数。对影响误差的因数进行了讨论。并按照所得结论在优化双圆弧算法[4]基础上对算法进行了改进。

1 优化双圆弧拟合模型

1.1 双圆弧拟合方法

双圆弧的拟合方法常用的有3种：第1种是以三角形的内心作为双圆弧的联接点，称为内心法。第2种是将双圆弧的联接点选在样条曲线上，称为交点法。第3种方法是采用改变双圆弧联接点的切线斜率使双圆弧曲线与样条曲线之间的法向误差达到最小，又称优化双圆弧拟合。内心法计算简便，但误差不易控制在允许范围内；交点法的误差较小，但是由于要解四次非线性方程，计算复杂；优化双圆弧计算简便，线性，稳定性好，十分适于运用到数控加工。本文以优化双圆弧作为曲线轮廓工件加工时拟合算法，并通过调节分段数和每段联接点斜率来减小误差，达到拟合的优化设计。为了找出较适合的斜率，将使用随机数生成斜率值并计算相应的误差，通过误差与最大允许误差的比较选出适合的斜率。

1.2 优化双圆弧拟合算法

设由测量或实验所得的一组离散有序的点列Pti(xi,yi)(i=1,2,…,n)形成一条样条曲线，称目标曲线。设目标曲线相邻两个节点为Pti、Pti+1(i=1,2,…,n)，现在不妨在曲线上取两点来做研究。设已知两节点坐标为P1(x1,y1),P2(x2,y2)，经过P1、P2点的曲线切线斜率为T1、T2（图1），并设T1＞T2，两切线的交点为P3，设ΔP1P3P2三边长a=，b=、c=，若已经取定一数值TN(T1＞TN＞T2)作为双圆弧拟合公切点的切线斜率，则有

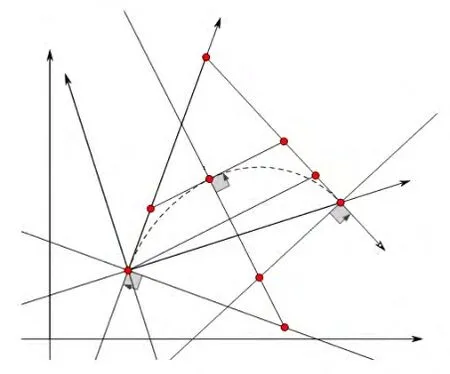
图1 优化双圆弧拟合基本原理

（1）过1P作斜率为TN的直线交P23P于P4，此时我们可以求出已知量d=、e=；

（2）假设已经找到双圆弧公切点P5及公切线P6P7，注意P6∈P1P3、P7∈P2P3，则有关系P6P7//P1P4，下面我们确定P6，进而确定P5的位置；

（3）设m=，由关系P6P7//P1P4，由文献[4]有设n=，易得

当d＞e时有m＞0，可在P6P7上求得符合条件的公切点P5点，上式成立。当d＜e时则有m＜0，这时P6在P1P3的延长线上，无法求出公切点P5。此时应该取P2为基点，过P2点作斜率为TN的直线，同理相反方向作图即可。若T1＜TN＜T2，出现d＜e的情况同理。

（4）设O1、O2分别为两个圆弧的圆心，r1、r2为两圆弧的半径。有O1P1⊥P1P3、O2P2⊥P2P3、O1P5⊥P6P7。且有P1P6=P6P5、P5P7=P7P2，从而可以作出双圆弧。

按照以上结果，将优化双圆弧拟合算法作为曲线拟合时求解的数学模型。应用VB编写双圆弧拟合计算子函数，函数需要5个已知变量，在代码中命名如下：两个节点的坐标值(x1,y1)、(x2,y2)及对应的切矢ks和ke，TN值则由联接点切线与节点连线的夹角rr=∠P3P1P2来间接表示。函数运行后返回输出对应两圆弧的圆心坐标、联接点坐标和圆弧半径，在代码中表示为xo1,yo1,xo2,yo2,xn,yn,r1,r2。另外，函数中定义数组x(i)、y(i)用来存储曲线上每段圆弧端点的坐标值，用于函数中的计算及双圆弧曲线的绘制。函数名：Function shuangyuanhu(x1,y1,x2,y2,ks,ke,rr,xo1,yo1,xo2,yo2,xn,yn,r1,r2)。再通过圆弧绘制命令：Call draw_Arc(x(i),y(i),xn,yn,xo1,yo1)Call draw_Arc(xn,yn,x(i+1),y(i+1),xo2,yo2)绘制两段圆弧即可实现曲线轮廓工件的双圆弧拟合。

1.3 双圆弧误差分析及切线斜率TN选取

曲线轮廓工件双圆弧拟合分析误差时，计算原曲线和双圆弧拟合曲线之间的法向误差：

以每相邻两型值点为一个单元进行讨论，可在型值点间取10个等分点，若等分点在以O1为圆心的圆弧上时，法向误差为

若等分点在以O2为圆心的圆弧上时

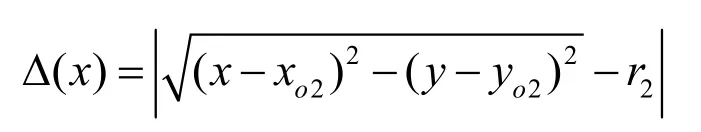
设允许的最大误差为Δ允，当ΔX＜Δ允时，双圆弧合格，反之则不合格[5]。若双圆弧不合格要改变TN值重新拟合直到双圆弧合格为止。

2 双圆弧拟合误差分析

2.1 双圆弧拟合实例

例：用数控车床加工某回转体工件时，设工件的母曲线方程为二次方程y=0.213157×x-0.50216×10-3×x2其中x∈(0,170)。

这里不妨先按步长为10，各段双圆弧的TN值为随机生成的方案进行拟合。运用编写的程序画出双圆弧拟合曲线图如图2所示。

图2 双圆弧拟合实例

2.2 误差分布和简单优化

在VB的窗口中绘制法向误差图表，以x值为横坐标，每组双圆弧对应的最大误差值为纵坐标，画出误差分布如图3所示，并在图中标出允许误差值Δ允，令Δ允=0.007μm。图3可以直观地观察双圆弧曲线各部分误差情况。

图3 误差分布图

误差分布图显示出这次的拟合有4段曲线是不合格的，要重新选择每段的TN值，并重新拟合。设置误差判断条件，当误差不满足条件时重新生成TN值，如此重复循环，直到法向误差符合要求为止。拟合优化程序框图如图4所示。

图4 拟合优化程序框图

进行TN值的重选和双圆弧曲线再拟合就可以得出基本符合要求的双圆弧拟合曲线如图5所示。

图5 重选TN值后的误差分布图

运用重选TN值求解双圆弧曲线计算量大且常会出现难以收敛导致程序无限循环的问题。因此应该从误差的规律入手寻求更简单高效的拟合方案。

3 影响误差的因素

上例是以步长为10这一条件为前提进行研究的，所以TN值成为影响曲线拟合精度的唯一变量。但由于双圆弧拟合曲线的形状是由各段基点位置及其TN值共同决定的，所以对双圆弧拟合方案求最优解将是一个多元非线性问题。这里我们将问题简化，固定其中一部分条件研究其他条件对双圆弧拟合的影响。

3.1 TN取值的对误差的影响

这里先固定各节点位置，以便直观的研究TN值对拟合误差的影响。由图1可见端点及其对应的切矢固定时，取不同TN值将获得不同的拟合曲线，在ΔP1P3P2包围的区域内有无数解。

不妨分别按照P1P2斜率和黄金分割率来确定TN值来观察拟合效果。

（1）平行弦法确定TN值

平行弦法是指取TN值等于P12P斜率，这时点4P与2P重合，直线P6P7平行于直线P12P。图6(a)为上例曲线采用平行弦法双圆弧拟合时得出的结果。该曲线使用平行弦法拟合的最大法向误差为1.96E-6mm，情况比较理想。

（2）黄金分割法确定TN值

在T1，T2间按黄金分割率0.618取值作为TN值，图6(b)为上例双圆弧拟合时得出的结果。

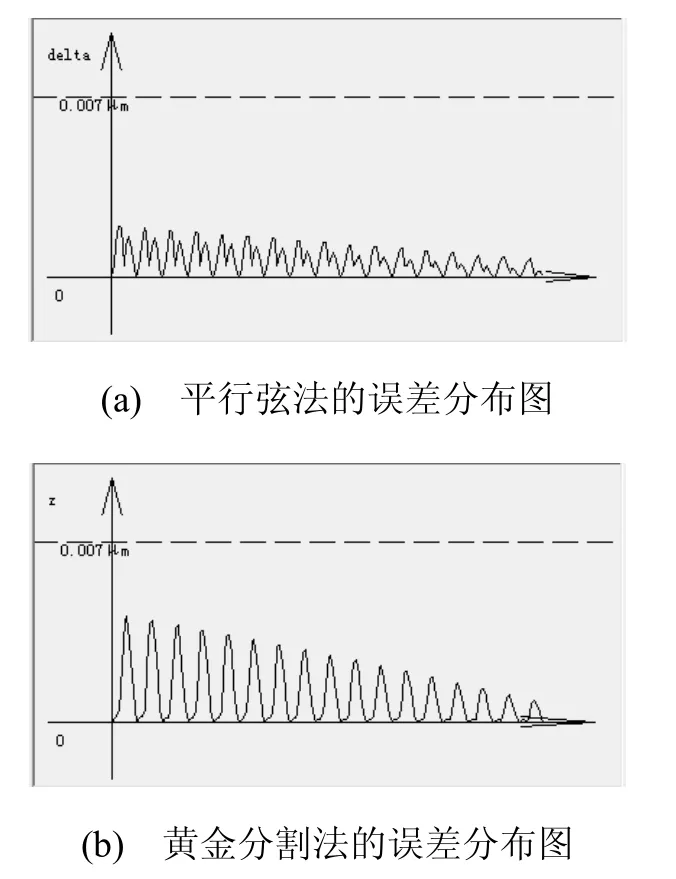
图6 不同TN值对应的误差分布图

TN值确定了双圆弧拟合曲线的形状，进而决定了误差的分布。在确定基点的情况下，调节TN值可以减小误差。

3.2 分段数对误差的影响

（1）减少分段数，增大步长

将上例中步长10，改为步长19进行双圆弧拟合，为了减小其他变量的影响，TN按照平行弦法取值，所得结果如图7(a)与图6(a)比较可知双圆弧拟合的误差增大，超出了允许值。

（2）增加分段数，减小步长

将上例步长改为步长15.4mm进行双圆弧拟合，TN按照平行弦法取值，所得结果如图7(b)，与图6(a)比较，误差减小，拟合精确度提高，法向误差降低为6.89E-06mm，刚好达到要求。

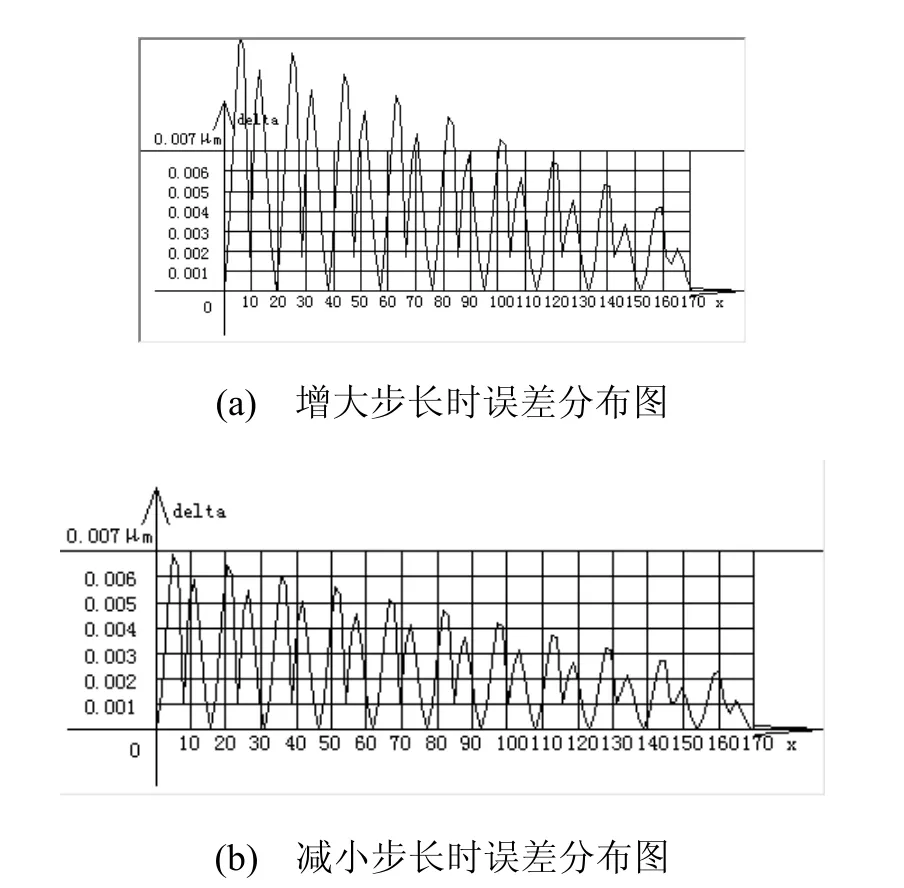
图7 改变步长时误差分布图

经过多次改变步长获得多组误差分布图后发现步长15.4mm是临界步长，相应分段数为11段。当所选步长小于15.4mm时双圆弧曲线都能满足要求。

4 改进的双圆弧拟合算法

4.1 误差值变化规律分析

比较图6(a)和图7(a)时可以发现，尽管所取的分段数不同，其误差曲线波动趋势基本相似。这是由于采用平行弦法确定TN值时，双圆弧拟合曲线将只由两节点及其切矢决定，也就是说此时拟合误差将只受节点选取的影响。

改变步长就相当于改变了节点的选取。通过减小步长来减小误差虽然效果明显，但是常常会引起大部分曲线段精度过高同时过小的步长会使分段数增多。在具体的曲线拟合中，对于给定的误差,往往要求用尽量少的圆弧段数[6]，因此单纯通过减小步长来控制误差不一定是可取的。

4.2 基于步长规划的优化算法

结合平行弦法和改变步长的方法来进行优化，在采用平行弦确定各段TN值的前提下，根据曲线的拟合误差分布情况来重新规划各分段所使用的步长，使拟合曲线的最大误差值低于允差的同时避免出现精度过高的情况并降低分段数。步长规划算法：

设第i段的两个基点为Pti、Pti+1(i=1,2,…,n)。两点间的步长为Li测得满足拟合条件的临界步长Lc以及能使大部分曲线段不合格的较大步长Lb，Li的取值范围为Lc＜Li＜Lb。则两基点的坐标为：

拟合曲线时，比较该段双圆弧曲线拟合的最大法向误差，当最大法向误差Δmax＞Δ允时，选用更小的Li重新拟合。当最大法向误差Δmax过小时则增大Li，这样将使Li自动向理想值逼近，直到双圆弧曲线符合要求为止并继续拟合下一段曲线。步长规划的程序框图如图8所示。

图8 步长规划程序框图

该程序运行后将自动生成各分段的步长并绘出相应的双圆弧曲线。

对于上例中的曲线，按照第三部分的实验结果，Lc取13mm，Lb取20mm。

运行程序生成各段步长14.11，14.62，15.21…19.39，共生成10段。拟合曲线误差如图9所示。

图9 上例改进的拟合误差分布图

与图7(a)的情况相比，分段数同为10段，采用变化步长的拟合曲线没有超出允差。最大误差为：6.77E-06mm。误差较之前分布更加均匀且没有出现精度过高问题。

实验证明规划步长拟合法可以用较少的分段数拟合出符合允差的双圆弧拟合曲线，计算量少，更易于实现工件的轮廓曲线的加工。

5 结束语

本文运用VB实现优化双圆弧算法的计算机模型，对拟合误差进行了计算和分析。讨论了影响拟合误差的因素，并在此基础上提出了双圆弧拟合的改进算法，通过步长规划方法改进双圆弧曲线的拟合，保证了较低的计算量、较少的步长以及允许的加工精度，使拟合曲线的获得更简化，更有利于计算机的编程和硬件实现。

[1]沈纪桂.数控加工圆弧拟合的优化方法[J].机械工程学报,1997,(6): 64-69.

[2]苏步青,刘鼎元.计算几何[M].上海: 上海科学出版社,1981: 195-203.

[3]丁克会,席平原,周红斌.参数方程曲线的最优逼近算法及实现[J].机械传动,2008,(6): 57-59.

[4]沈纪桂,方志梅,李凌丰.优化双圆弧拟合[J].工程图学学报,1995,(1): 53-56.

[5]郭文兰,张 彤.曲线方程的双圆弧拟合算法及实现[J].哈尔滨理工大学学报,2004,9(6): 87-89.

[6]虞铭财,杨勋年,汪国昭.整体最优双圆弧拟合[J].高校应用数学学报A辑,2004,19(2): 225-232.