八心圆弧拟合椭圆误差的理论解析及最优解

2014-03-29王国顺唐立波

图学学报 2014年5期

王国顺，唐立波

(大连交通大学机械工程学院，辽宁大连 116028)

针对用圆弧拟合椭圆的误差分析没有精确理论解析这一现状，根据椭圆图形本身的特性，利用图形学理论，提出了等差拟合弧的概念，在给定椭圆长短轴的情况下，就可以推导出八圆弧拟合椭圆误差的理论解析表达式，该解析式是关于法向误差变量的超越方程，为求解超越方程，首先确定了定解区间，然后利用数学中的二分法对其求解。对于一个具体给定的椭圆，可以求出使用八心圆弧拟合的法向最小误差，即八心圆弧拟合的最高精度，如果要求更高的拟合精度，只能通过增加拟合圆弧的数量来实现；计算过程采用AutoCAD软件内嵌的Visual LISP语言编程实现。在数控加工中，采用拟合圆弧作为刀具的运行控制轨迹，加工出来的曲线总是存在一定的误差，为此，只能将椭圆误差控制在允许的变动范围内，该范围定义为椭圆公差带[1]。彭云柯[2]采用约束非线性切比雪夫逼近论，给出了一种用四段圆弧逼近椭圆的方法，可使最大逼近误差达到最小，从而提高了数控机床和机器人的椭圆加工作业的精度，并且提供了最佳半径的相当准确的近似计算公式可作为最后结果使用，从而避免编程迭代。周晓铭等[3]发现人们对于圆弧插补的研究，针对大多数集中在圆弧逼近算法本身而没有考虑机床的最大切割半径，一旦拟合圆弧半径大于机床半径时，机床不能处理的情况，提出了一种新的基于二分法的曲线圆弧拟合方法，该方法继承单圆弧等弦高误差控制法和传统二分法取中点的习惯，以最大弦高点为节点分割曲线，以相邻三节点作圆弧拟合曲线，在拟合半径大于数控系统能处理的最大半径时，用两直线拟合该段圆弧，方便数控自动编程。樊琳[4]研究了列表曲线拟合问题，根据已给出曲线上某些坐标点，由曲线坐标离散的型值点来描述工件表面形状曲线的大致走向，但没有给出方程。韩鸿鸾[5]、丁克会和席平原[6]分析了四心圆弧拟合椭圆的偏差变化规律，给出的误差是沿椭圆的拟合圆弧径向。这与椭圆实际要求控制的法向误差不完全一致，因而不能准确描述四心圆弧拟合椭圆的精度，拟合的近似程度较模糊。沈纪桂等[7]介绍了传统的曲线拟合方法，即单圆弧一次逼近法、两次逼近法和双圆弧一次逼近法，上述三种方法中，两次逼近法和双圆弧一次逼近法中的双圆弧均是在两相邻型值点间进行拟合，其拟合圆弧段数多，计算、输出的数据量大，而单圆弧一次逼近法虽采用大跨距拟合，但具有一定的盲目性，拟合精度差。王林鸿和陈永辉[8]研究了用传统的四心圆法作近似椭圆与实际椭圆的误差分布规律，结果表明，除椭圆的四个交点以及与坐标轴的四个交点外，处处存在偏差，其中大圆弧段偏差较小，小圆弧段偏差最大，近似椭圆比精确椭圆面积大，椭圆越扁平，偏差越大，在极端扁平的情况下，最大偏差超过长半轴的3%、短半轴的15%。文献[9-11]研究了数控加工领域中的关于椭圆及曲线拟合的很多方法，普遍认为，根据曲线段斜率变化规律确定圆心方位、以凸弧代替凸曲线的等弧长圆弧拟合方法是可行的，并在该方法中使用了级数展开来简化超越三角方程，避免了迭代求解的麻烦，这种方法的不足是没能从理论上给出拟合误差的解析式，因而不能更好的描述拟合精度。文献[12-14]认为双圆弧方法适用于对数量较大的实验数据作近似拟合，该方法在数控加工及图形绘制中可以得到较好的应用，双圆弧曲线是一阶连续的，数控加工后零件的光滑度好，从而，它可有效地对任意列表平面曲线和空间曲面作数控加工。唐立波等[15]给出了四心圆弧拟合椭圆的解析算法及其最优解，但是拟合精度更高时无法满足。

综上所述，研究侧重在数控加工应用领域；在圆弧拟合椭圆或曲线方面的理论研究很多，已有的研究一般是采用双圆弧或其他一些近似拟合方法，而没有给出关于误差的精确解析，致使拟合误差大，精度低，导致数控加工效率低，时间长，从而增加了产品的成本。本文导出的解析超越方程，填补了八心圆弧拟合椭圆法向误差理论解析的空白。

1 八心圆弧拟合椭圆的边界条件与约定

椭圆的参数方程：

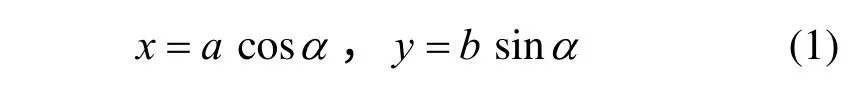
其中α为椭圆的参数角，0°≤α≤360°，a、b为横、纵半轴长，b＞a＞0，且a≠b；如果a=b，则为圆的参数方程。由于椭圆具有对称性，故以下只按a＜b时第一象限的椭圆分析推导解析式，其他象限可由第一象限的结果作对称变换获得，a＞b时，可交换a、b求解，然后将结果相对直线x=y作对称变换。为了较好地逼近理想椭圆(如图1)，依据椭圆的特点，八心圆弧拟合椭圆应同时满足以下5个边界条件：

(1) 过椭圆端点；

(2) 相对椭圆中心对称；

(3) 保持一阶导数连续；

(4) 在给定的椭圆公差带内；

(5) 分段拟合圆弧的半径变化趋势与椭圆的曲率半径变化趋势一致。

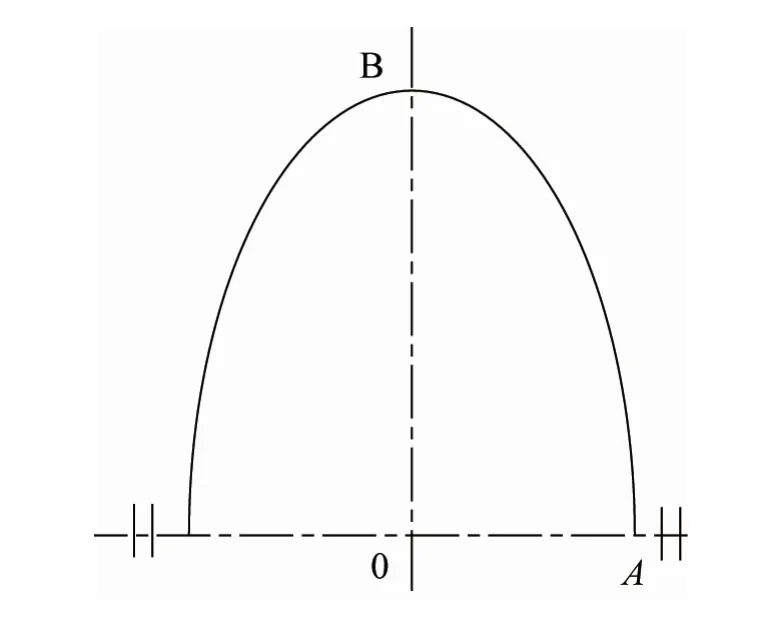
图1 椭圆(1/2)

给定椭圆法向误差δ(为讨论方便，以下取δ>0)时，可以确定椭圆内外两条等距线，如图2所示，两条等距线确定的范围称椭圆的误差范围，若此范围与椭圆的公差带相同，则这个误差范围就是椭圆的公差带。

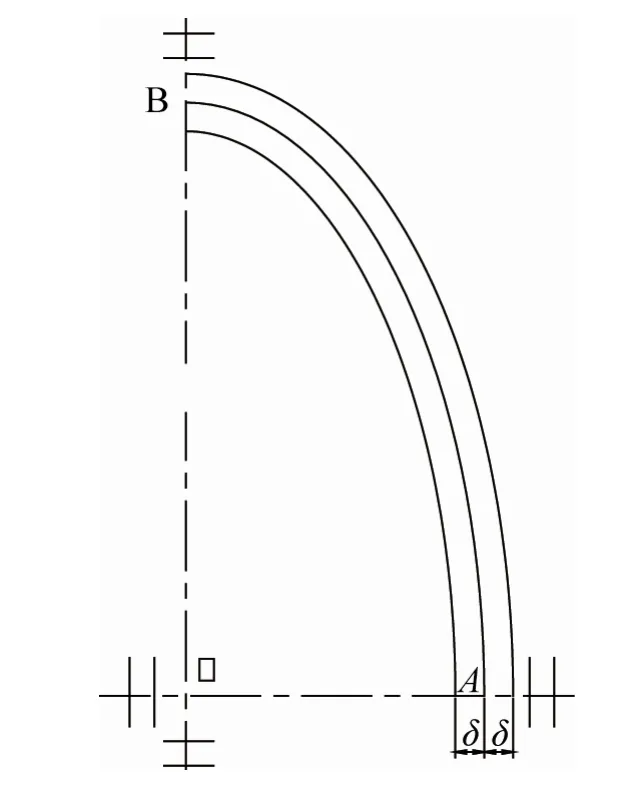
图2 椭圆法向误差δ

八心圆弧拟合椭圆，满足上述条件下在第一象限共分三段，如图3所示。其中，过横轴端点的圆弧半径最大，称为大圆弧；过纵轴端点的圆弧最小，称为小圆弧，剩下一段圆弧称为中间圆弧。

图3 拟合圆弧名称

为便于讨论，本文中的字母O、R、tP分别代表圆心、半径和切点，小圆弧对应的变量符号角标用1表示，大圆弧对应的变量符号角标用2表示，中间圆弧对应的变量符号角标用3表示，圆心对应的坐标分别为：xo1,yo1、xo2,yo2和xo3,yo3，其中xo1=yo2=0。

2 椭圆的等差拟合圆弧

2.1 定义

在一个椭圆给定法向误差δ时，分别切于δ所确定的椭圆内外两条等距线的圆弧定义为椭圆等差拟合圆弧(如图4中Pt、Pt1之间的圆弧)。

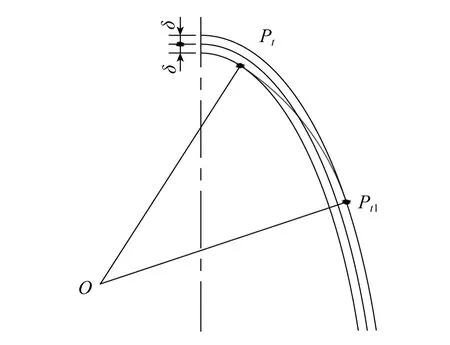
图4 等差拟合圆弧

在区间[0,δ0]上取任一误差δ，则区间[0,π/2]上任一参数角α对应椭圆上一点P，则椭圆上过点P的法向斜率：

过点P的法线方程：

再取区间[0,α]上任意一参数角α1，α1对应椭圆上一点P1，则过点P1的法线方程：

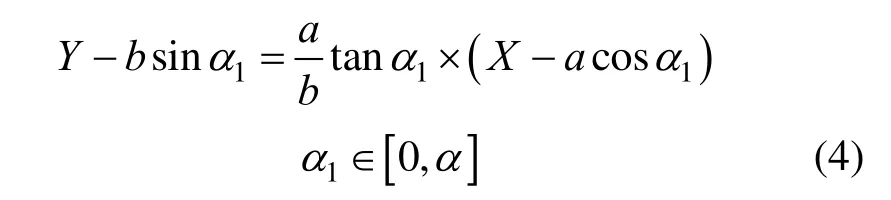
式(3)和式(4)联立求解，可得交点O，其坐标：

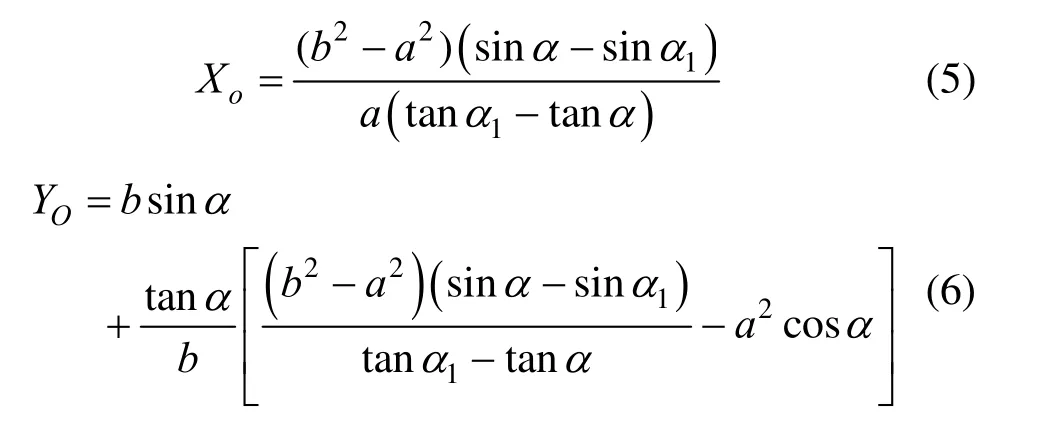
OP交椭圆内等距线于点tP，O1P交椭圆外等距线于点Pt1，若：

则Pt、Pt1是在以O为圆心的同一个圆上，根据上述等差拟合圆弧的定义可知，此时以Pt、Pt1为端点的圆弧是椭圆的一等差拟合圆弧。以下称Pt为等差拟合圆弧的左端点；称Pt1为等差拟合圆弧的右端点。

2.2 椭圆最小等差拟合圆弧

根据上述等差拟合圆弧的定义，当α=π/2时，等差拟合圆弧最小，其左端点是纵轴与椭圆内等距线的交点Pt(0,b-δ)，如图5所示。

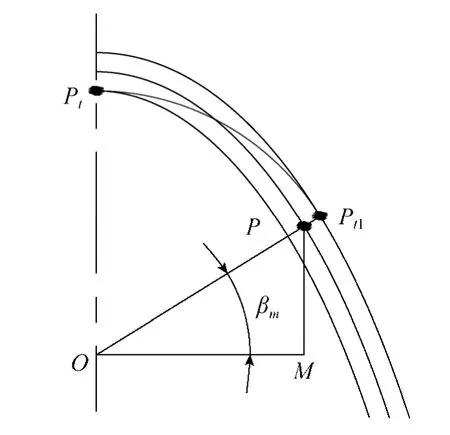
图5 最小等差拟合圆弧

设右端点对应的椭圆参数角为αm，过O和OPt1与椭圆的交点P作辅助线交M，由图示关系可知OPt1的斜率：

将式(2)代入式(8)可得：

故最小等差拟合圆弧的圆心纵坐标和半径分别为：

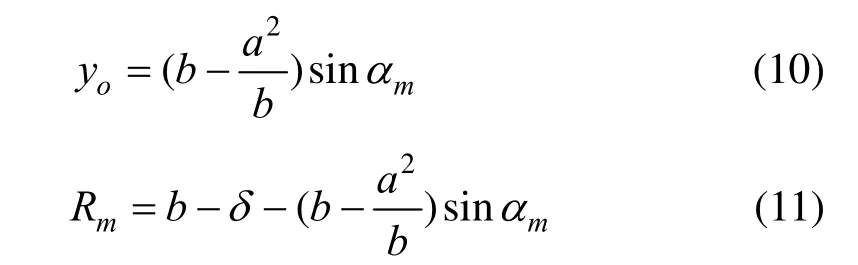
Pt1的坐标为：

由式(9)～(12)可以看出，只要能求解mα，最小等差拟合圆弧即可确定。为此，由式(7)和图5所示几何关系可得：

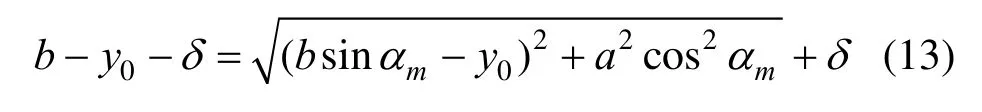
将式(10)代入化简可得：

该方程是关于sinmα的一元二次方程。由于设定在第一象限求解，sinmα大于0，故舍去负解，将所得sinmα的正解化简，根据反三角函数关系可得：

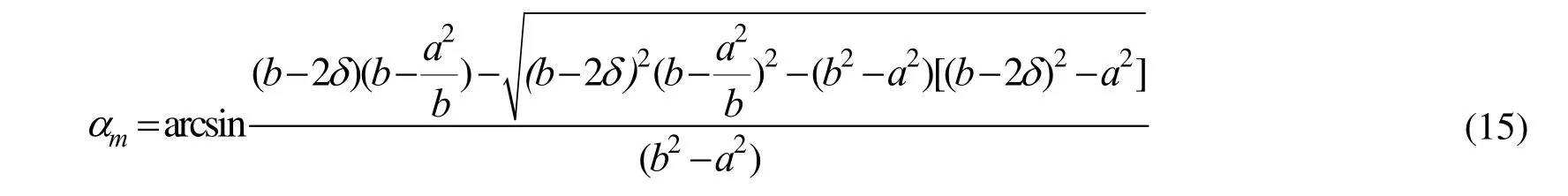
综上所述，最小等差拟合圆弧由a、b、δ确定。

2.3 椭圆最大等差拟合圆弧

当α1=0时，等差拟合圆弧最大，其右端点是横轴与椭圆外等距线的交点Pt1(a+δ,0)，如图6所示。

图6 最大等差拟合圆弧

参照最小等差拟合圆弧的解析方法，求解出αn，从而最大等差拟合圆弧即可确定，αn的解析表达见式(17)。

设左端点Pt对应的椭圆参数角为αn，过O和OPt与椭圆的交点P作辅助线交N，由图示关系可知OPt的斜率：

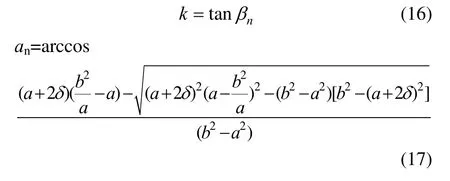
2.4 椭圆等差拟合中间圆弧的求解

根据上述分析，给定椭圆法向误差δ时，等差拟合圆弧的左端点所对应的椭圆参数角的定解区间是：α∈[αn,π/2]；右端点所对应的椭圆参数角的定解区间应是：α1∈[0,αm]。若α1=0，α=π/2，则椭圆的最大、最小等差拟合圆弧重合，其圆心在原点，设此时对应的法向误差为δ′，由式(13)可得：

显然，法向误差δ≤δ′时，才存在等差拟合圆弧，进而在区间[αn,π/2]上任取α，由式(3)～(6)联立求解α1可确定一个等差拟合圆弧。但式(3)～(6)联立得到的是关于α1的超越方程，为此，设：

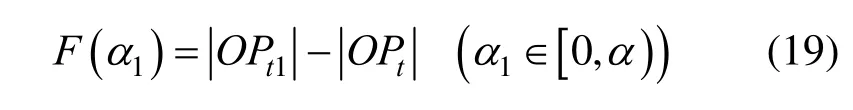
根据该式绘制F(α1)的变化曲线得到的结果如图7所示，可以看出F(α1)在区间[0,α)上关于α1是单调减函数，且F(0)＞0，α1趋向α时F(α1)＜0，故可在区间[0,α)上用二分法[16]求解得到α1，至此，椭圆的等差拟合圆弧随给定的α完全确定。

图7 函数F(α1)随α1变化曲线

用同样的方法，在区间[0,αm]上任取α1求解α也可确定对应的等差拟合圆弧。

综上所述，在给定椭圆一个法向误差δ时，椭圆的等差拟合圆弧只与α或α1独立相关，将α、α1代入式(5)、(6)得出xo3、yo3。

3 八心圆弧拟合椭圆解析

3.1 八心圆弧拟合椭圆的定解分析

在区间(0,δ0)上给定一个法向误差δ时，拟合椭圆的大、小圆弧可按2.2节和2.3节的方法进行求解；中间拟合圆弧可按2.4节的方法求解，其两个端点所对应的椭圆参数角的定解区间为α∈[αn,π/2]，α1∈[0,αm]，在定解区间内，有无数个椭圆等差拟合圆弧，如果等差拟合圆弧分别与大、小圆弧内切，则这三个圆弧就可构成满足1节所述5个边界条件的八心拟合圆弧。

3.2 与小圆弧相切的椭圆等差拟合圆弧

区间[αn,π/2]上任意一参数角α对应的等差拟合圆弧可按2节所述求解，设其半径为R3，其圆心O3与小圆弧的圆心O1之间的距离为L1，则该等差拟合圆弧与小圆弧内切的条件是：

其中，

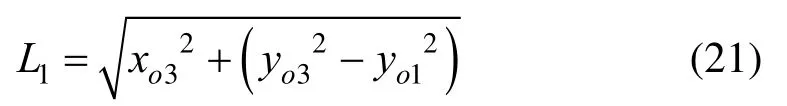
由2节可知，O3、R3均由α确定，故L1也由α确定，因此式(17)是关于α的独立方程，但导出此方程却是关于α的超越方程，为此，取

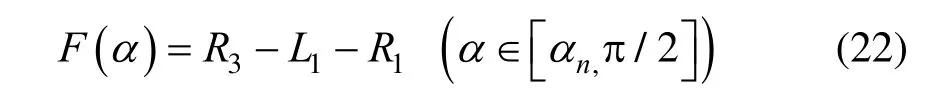
根据该式绘制F(α)的变化曲线如图8所示，可以看出F(α)在区间[αn,π/2]上关于α是单调减函数，且F(αn)＞0，F(π/2)＜0，故可在区间[αn,π/2]上用二分法[16]求解方程F(α)=0，得到α，其所对应的等差拟合圆弧即是与小圆弧相切的等差拟合圆弧。

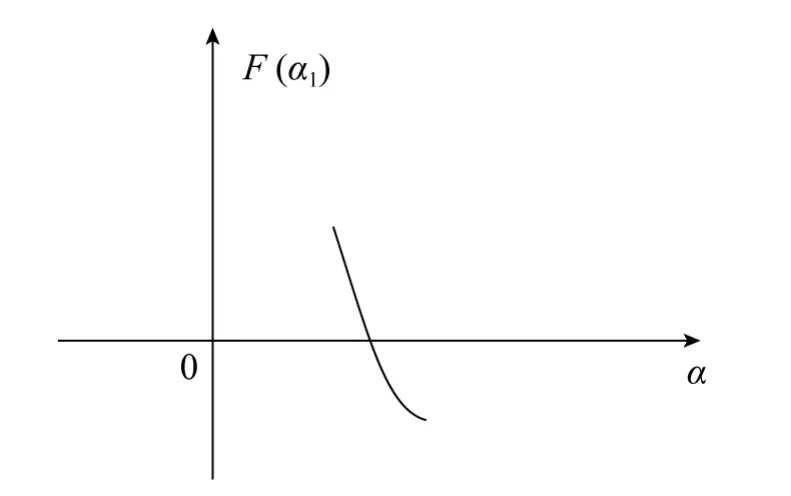
图8 函数F(α)随α变化曲线

3.3 中间圆弧求解

由3.2节可知，给定椭圆法向误差δ时即可求得与小圆弧内切的一等差拟合圆弧，设其半径为R3，其圆心与大圆弧圆心的距离为L2，则其与大圆弧内切的条件是：

其中，

该方程中的3个变量都只与δ相关，所以此方程是关于δ的独立方程，但导出此方程却是关于δ的超越方程，为此，取：

根据该式绘制F(δ)的变化曲线如图9所示，可以看出F(δ)在区间[0,δ0]上关于δ是单调减函数，且F(0)＞0，F(δ0)＜0，故可在区间[0,δ0]上用二分法[16]求解方程F(δ)=0，得到的解设为δ3，δ3所对应的等差拟合圆弧与大、小圆弧同时相切，是拟合椭圆的八心圆弧中的中间圆弧。

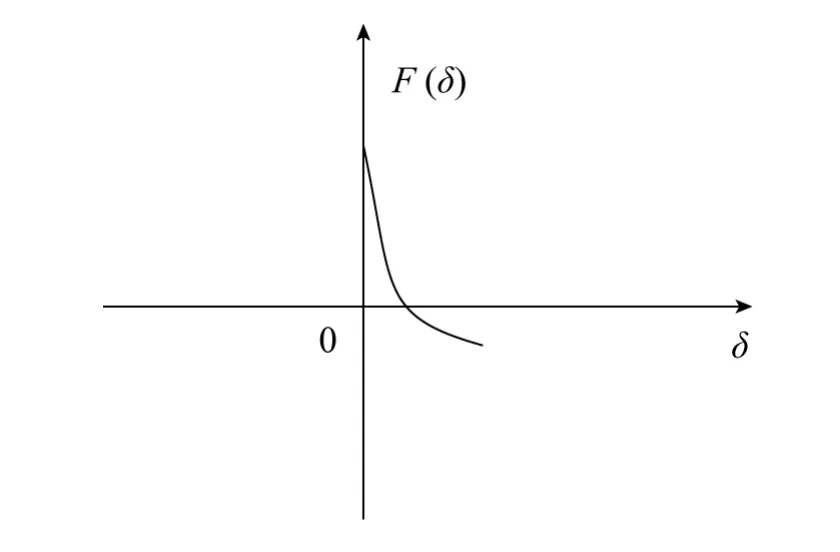
图9 函数F(δ)随δ变化曲线

上述解析采用Visual LISP语言编程，在AutoCAD环境下运行，可快速求得八心圆弧拟合椭圆的结果。

4 实例分析

按照上述方法，以长半轴b等于60，短半轴a分别取5、10、15、20、25、30、35、40、45、50、55的系列椭圆为例，编程计算的八心圆弧拟合椭圆的误差，结果见表1，误差分布见图10。

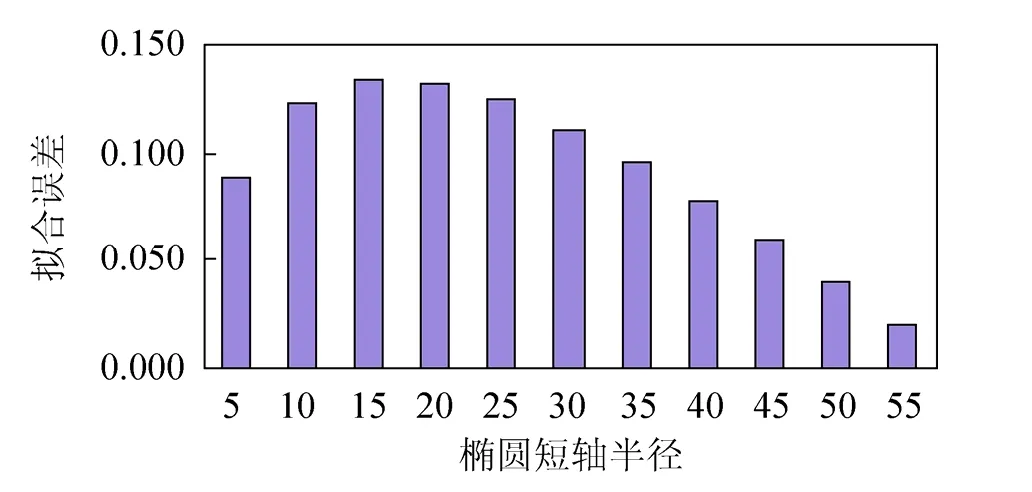
图10 误差分布图

从表1可以看出：对于某一固定的椭圆，δ是用八心圆弧拟合的最小误差，也是八心圆弧拟合所能达到的最高精度，如果要求更高的拟合精度，则必须增加拟合圆弧的段数；从图10可以看出：椭圆越饱满(即长、短轴相差较小)或极端扁平(即长、短轴相差甚大)时拟合精度高。

表1 八心圆弧拟合椭圆误差的计算结果

5 结论

椭圆的八心拟合圆弧有无数解。本文提出了椭圆等差拟合圆弧的概念，定义了等差拟合弧，从理论上推导出八心圆弧拟合椭圆时法向误差的超越方程，并使用二分法进行求解。上述方法能根据椭圆长、短半轴快速求出八心圆弧拟合椭圆的最大法向误差，即拟合精度，若拟合精度的绝对值大于或等于最小法向误差时均可用该八心圆弧拟合，若小于最大法向误差的更高精度椭圆是不能用八心圆弧拟合的，必须增加拟合圆弧段数，这就为八心圆弧是否可以拟合给定法向误差的椭圆提供了准确的判断依据。

将来会在此研究基础上，继续研究更多段圆弧拟合椭圆，以提高拟合精度，满足工程需求。

[1] 刘巽尔.形状和位置公差[M].北京: 中国标准出版社,2004: 34-55.

[2] 彭云柯.椭圆加工作业中的四圆弧切比雪夫逼近[J].机械工程学报,2004,40(12): 168-171.

[3] 周晓铭,陶俊才,秦海鸥.基于二分法的曲线等误差圆弧拟合算法及其应用[J].南昌大学学报(理科版),2008,32(1): 100-102.

[4] 樊琳.列表曲线的圆弧拟合[J].机械工艺师,1998,(12): 7-8.

[5] 韩鸿鸾.椭圆插补原理存在的缺陷[J].机械制造与研究,2006,35(3): 65-67.

[6] 丁克会,席平原.基于MATLAB的最大误差双圆弧逼近曲线的算法及实现[J].机械传动,2007,31(6):57-59.

[7] 沈纪桂,方志梅,查显亮.优化双圆弧拟合的曲面加工[J].宁夏工学院学报(自然科学版),1997,9(1):5-10.

[8] 王林鸿,陈永辉.用四心圆法作近似椭圆的偏差分析[J].机械工程师,2002,(8): 59-60.

[9] 朱虹,王立军,杨海.基于圆弧拟合的非圆二次曲线加工技术研究[J].机械设计与制造,2012,(12):227-229.

[10] 刘吉安,张平.非圆曲线的双圆弧拟合及数控加工的程序编制[J].机电工程技术,2009,38(6): 44-46,91.

[11] 姚必强,姚进.数控加工曲线的等弧长圆弧拟合方法[J].四川大学学报(工程科学版),2008,40(1):171-174.