面向链结构的烯烃聚合过程模型化方法

邱云霞，顾雪萍，冯连芳

（浙江大学化学工程与生物工程学系化学工程联合国家重点实验室，浙江 杭州 310027）

聚烯烃是重要的聚合物材料，具有机械强度好、耐化学药品性、耐水性和电绝缘性等特点。在农业、包装、电子、电气、汽车、机械和日用杂品等方面有广泛的用途。2012年国内的表观消费量达3 500万吨。聚烯烃的链结构，包括分子量分布、共聚物组成分布及序列分布等，决定了产品的性能。对于均聚物，分子量及分子量分布是重要的评价指标。平均分子量大的聚合物的强度性能较好，平均分子量小的聚合物则具有更好的加工性能。分子量分布是在平均分子量的基础上对聚合物链结构更进一步的描述，常有分布指数和分子量分布曲线来表示。分子量分布窄的聚合物有利于提高制品的机械性能，分子量分布宽则可以兼顾力学性能并提高聚合物的加工性。对于共聚物，共聚物组成分布和序列分布是其质量评判的重要指标。不同的组成分布一般会对应不同的性能。对于一定组成的共聚物，其精细结构—单体单元序列长短和单体单元连接顺序会直接影响其性能。如，对乙丙橡胶来说，分子链为无规分布才能充分发挥其橡胶弹性。然而，在目前的工业生产过程中，聚烯烃性能的监测指标仅为熔融指数和密度，其依据为平均分子量和支化度是分别与熔融指数和密度相关联的[1]，在特定的条件下可获得一些经验关联式。但是，熔融指数和密度远不足以表达聚烯烃的链结构特性，这导致基于熔融指数和密度的工艺条件优化、过程建模型、在线估计与先进控制（APC）的结果并不理想。因此，基于聚合反应和过程机理，面向聚合物链结构的建模方法，才能真实表征聚合过程和聚合物产品的特征，满足聚合过程在线估计和先进控制的要求。

1 均聚物的分子量及分子量分布

1.1 矩方法

烯烃配位聚合过程的基元反应包括催化剂活化、链引发反应、链增长反应、链转移反应以及链失活反应[2]。乙烯在Ziegler-Natta催化剂作用下的反应机理如表1所示。其中，C*代表活性位，Cd代表失活活性位，Dr代表链长为r的死聚物，H2代表氢气，M代表单体，Al代表助催化剂，I代表杂质，Pr代表链长为r的活聚物。

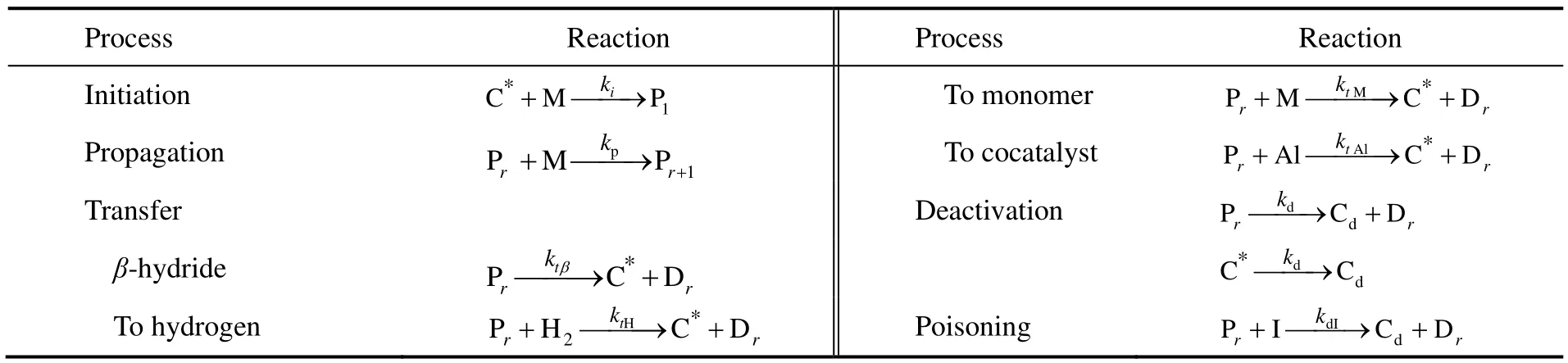
表1 Ziegler-Natta催化剂作用的乙烯均聚反应机理Table 1 The reaction mechanism of ethylene homopolymerization over Ziegler-Natta catalyst

部分组分反应速率如表2所示。理论上，依据工业过程中聚合反应器的组合与流动混合模式，写出各组分物料守恒方程便可通过求解常微分方程组从而得到聚合物的分子量分布[3]，但计算规模庞大。Ray等[4]在生成函数法的基础上采用了矩方法，使计算简化，矩的定义式为：

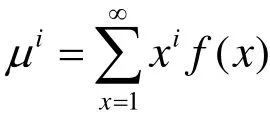
μi表示函数的i阶矩，x表示变量，f(x)表示函数。根据矩的定义，聚合反应中各组分的矩表达式如表3所示。根据表3，可分别得到数均分子量（Mn）、重均分子量（Mw）、分子量分布指数（PDI）与矩的关系式，如式（1），（2）和（3）。下表中，Xi和Yi分别代表死聚物与活聚物的i阶矩。

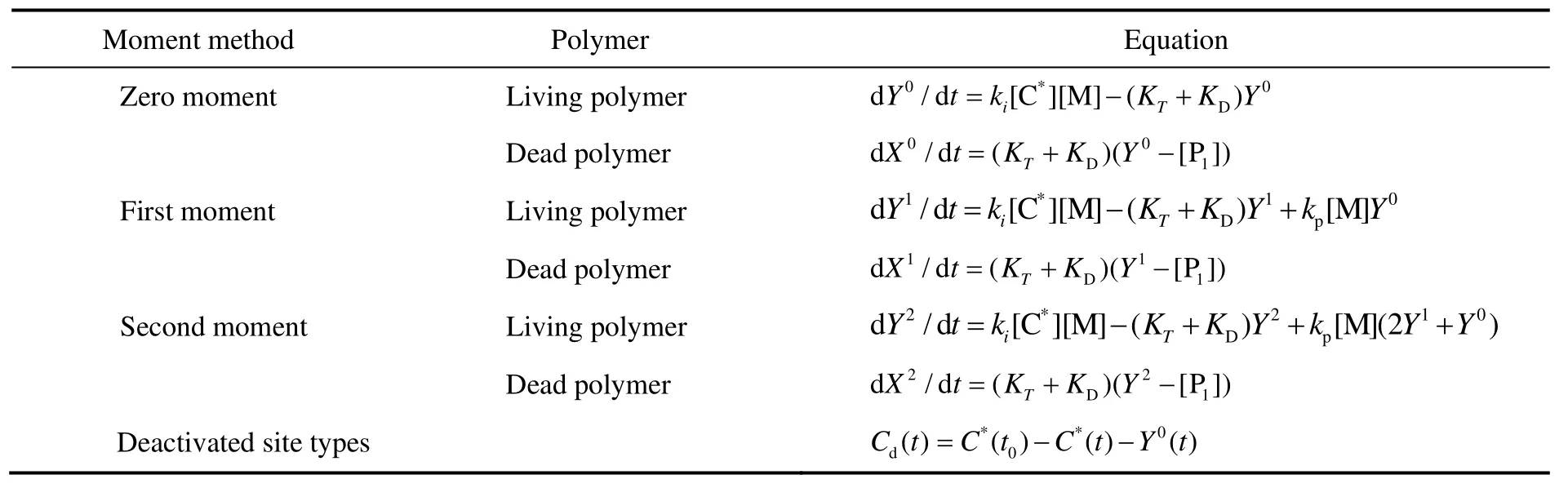
表3 各组分的矩表示方法Table 3 The moment equation of each substance

Note: KT=ktβ+ktH[H2]0.5+ktM[M]+ktAl[Al]; KD=kd+kdI[I].

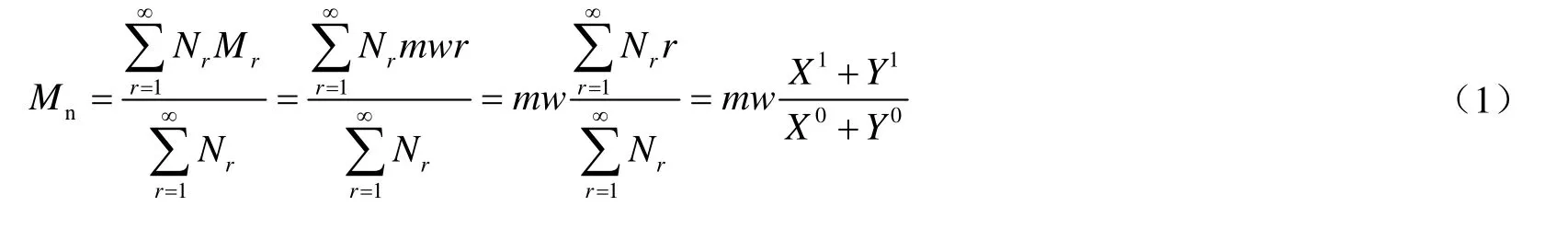
式中，Nr，Wr和Mr分别表示链长为r的聚合物链数、质量（kg）和摩尔质量（g·mol-1），mw表示共聚物中重复单体摩尔质量，Mn和Mw表示数均分子量和重均分子量，PDI表示分布指数。根据文献[3]，大多数烯烃聚合过程中，死聚物矩的含量远远大于活聚物，因此活聚物的矩可在计算中被忽略，使过程简化。

Hamielec等[5]利用矩方法分别模拟了自由基聚合下间歇、半间歇及连续过程。Soares等[6]对连续搅拌反应器中均相催化剂下烯烃聚合过程进行了建模与实验验证。McAuley等[7]将该方法用于了计算气相流化床生成聚乙烯的过程。

使用矩方法能得到平均分子量和分布指数，但对分子量具体分布却不能描述。

1.2 Flory分布

采用分子量分布函数方法能描述聚合物的分子量分布，比较前述矩方法，分子量分布函数可以描述更全面的链长分布。分子量的分布函数包括Schulz-Flory最可能分布、正态分布、Poisson分布和对数正态分布等。其中，Flory分布是目前被普遍使用的分布函数，它是单一参数τ的函数。

在烯烃聚合过程中，每个反应活性位分子量都服从Flory[8]分布。总的分子量分布是各活性位的加权累积。单个活性位Flory分布的表达式为：

式中，j代表在多活性位催化体系中的第j个活性位。

由式（5）可知，反应催化体系、氢气浓度和单体浓度是分子量及分布的主要影响因素。Soares等[2]通过实验发现反应中增加氢气进量会使反应加快，分子量分布变宽。

聚烯烃的分子量分布通常采用高温GPC测试表征，其结果用对数坐标表示，所以将Flory分布进行数学变化后得到如下对数坐标形式[9]。

聚合物总的链长分布是每个活性位所生成聚合物链长分布的叠加，如下式所示：

根据Flory的定义式，可得聚合物的数均链长与重均链长的表达式：

假设烯烃聚合反应器的流混模式符合全混流（CSTR），根据Flory分布，反应器中给定的时间t0到tp下的分子量分布，有以下表达式[10]。

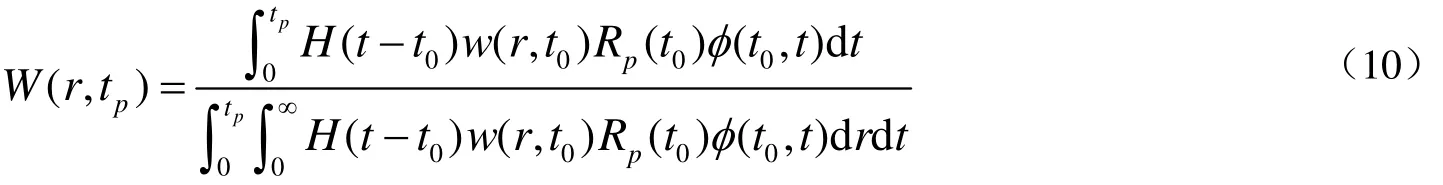
其中，φ(t0，t)是与停留时间有关的变量，表示从时刻t0到停留时间t时，生成的聚合物在反应器中的残留百分数。w(r，t0)代表t0时刻的瞬时分布，RP(t0)代表t0时刻的反应速率。

至此，将式（4）与式（10）联立，便可得到在CSTR中任意给定时间下聚合物链长的分布。同理，可结合其他反应器的停留时间表达将Flory分布应用于其他生产体系和过程。

Soares等[11]基于多活性催化体系聚合物的分子量分布是各活性中心分子量分布的加和的原理，通过选择不同的茂金属催化剂在同一负载上进行烯烃聚合反应，从而获得符合分子量分布设计预定要求的聚合物。Soares的研究中所用催化剂分别为Et[Ind]2ZrCl2和CpHfCl2，催化助剂为MAO，SiO2负载。Flory分布可叠加性的理论依据表示为：

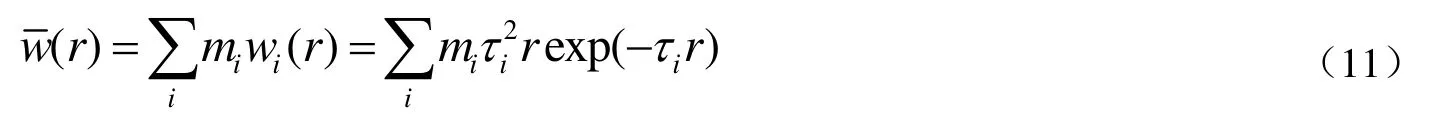
式中，i表示第i个活性位，mi表示在第i个活性中心上生成的聚合物的质量。

分别采用两种催化剂单独合成聚乙烯、以两种催化剂（Zr和Hf物质的量之比为0.36）复合合成聚乙烯，以及复合催化剂在不同乙烯压力下聚合[11]。结果表明，Flory分布不仅可以用于多活性中心烯烃聚合的分子量分布表达，也可以通过实验设计将单活性位活性中心催化剂进行复合，从而得到符合预期的分子量分布。

利用Flory分布的可叠加性方法，研究者对工业规模的聚烯烃装置进行了流程模拟研究。顾雪萍等[12]基于反应动力学对淤浆聚乙烯生产装置进行了流程模拟，用Flory分布的叠加性原理将多活性中心催化剂下合成聚合物的分子量分布确定为多活性位分子量分布的叠加，采集工业装置的数据与样品，结合高温GPC的分子量分布表征与Flory分布分峰，确定了Ziegler-Natta催化体系下活性位个数为5，构建了乙烯淤浆聚合工业流程的多活性位动力学动态模型，模拟计算得到的聚合物分子量分布与工业装置的分析数据十分符合。顾雪萍等[13]进一步以乙烯淤浆聚合工艺为研究对象，基于聚合机理，分别以聚合物的平均分子量和分子量分布为目标，以循环气中氢气乙烯比为决定变量，采用稳态优化方法求聚合物生产的工艺条件，结果表明以分子量分布曲线作为目标的优化方法明显比常规的以平均分子量为目标的优化方法优越。

2 共聚物分子量分布及组成分布

2.1 表观动力学参数模型描述分子量分布

烯烃配位聚合过程的基元反应有催化剂活化、链引发、链增长、链转移以及链失活反应[2]。在共聚物中，链增长反应为4个。下表是共聚反应机理，字母A和B代表两种不同的单体。

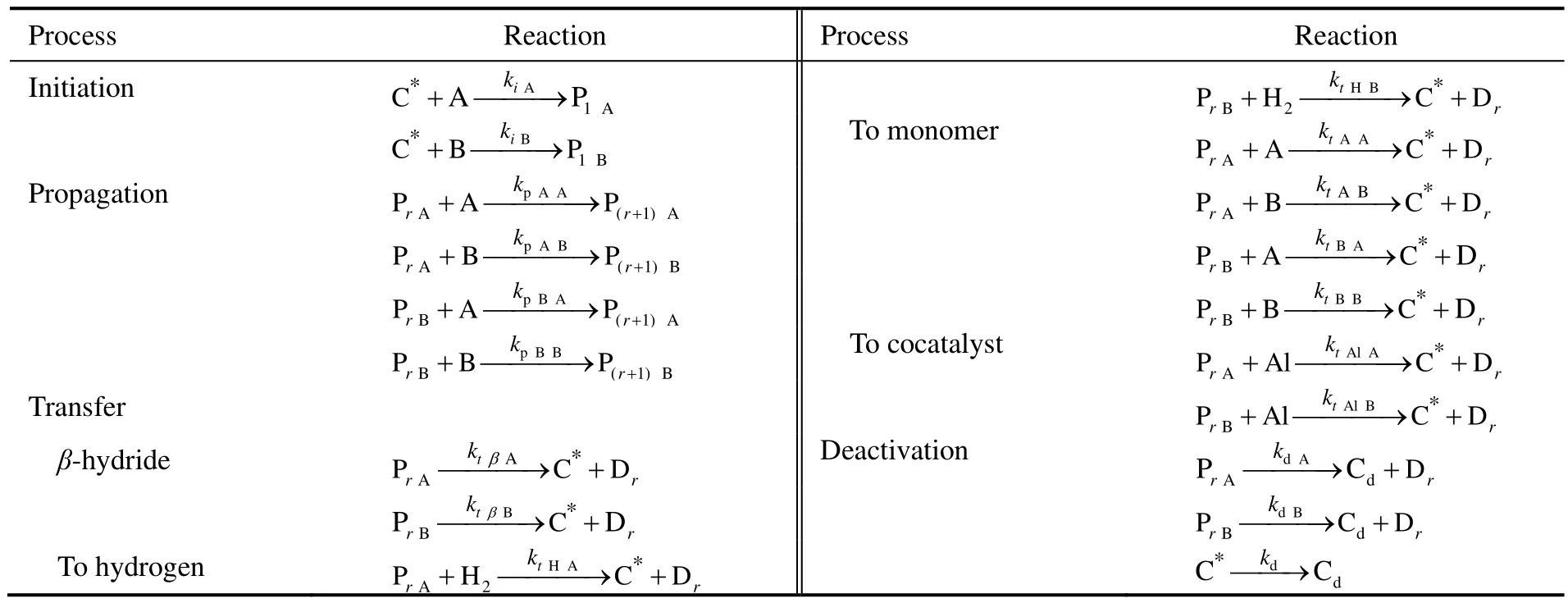
表4 配位聚合共聚反应机理Table 4 The reaction mechanism of coordination copolymerization

总活性链浓度随时间变化的表达式可以写成：

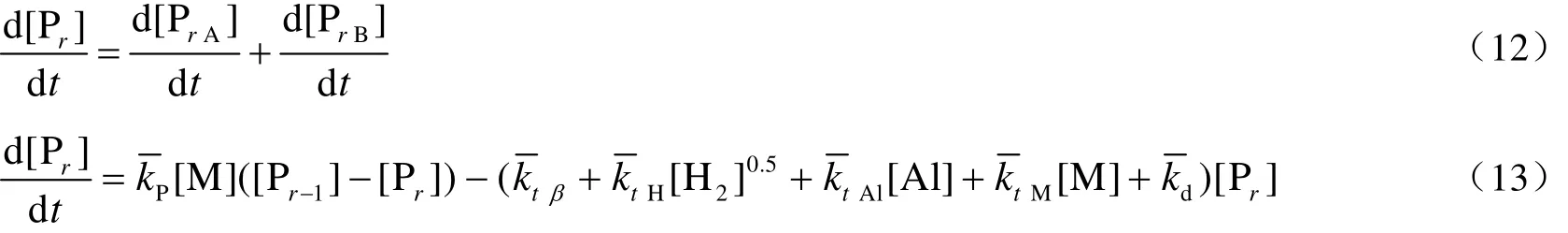
表5 表观动力学参数表达式Table 5 The equation of pseudo-kinetic parameters

同理，Flory分布对于共聚物也可用同样的方法。Xie等[14]将“表观动力学参数模型”应用于自由基共聚反应中，并成功得到了线型共聚物的分子量分布。

郑耸[15]在研究高密度聚乙烯（HDPE）的动态建模时，利用共聚物的Flory分布确定了5个催化剂活性位，整定了各活性位的动力学数据，并与工厂产品数据进行对比，结果比对良好。

2.2 用Stockmayer分布描述共聚物组成分布

Stockmayer二元分布函数被用来描述单个活性位上生成共聚物的共聚链长与组成分布[16]。

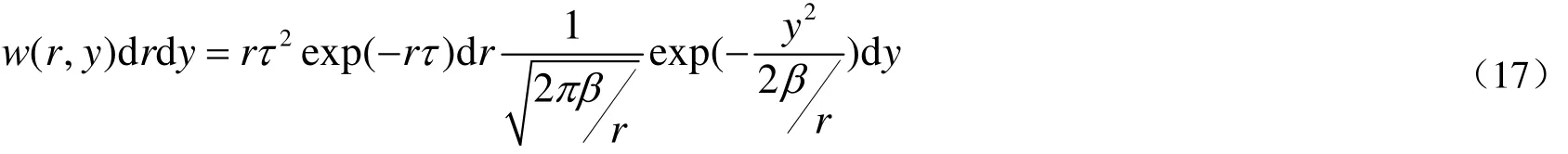
将Stockmayer方程链长对dr积分得[16]：

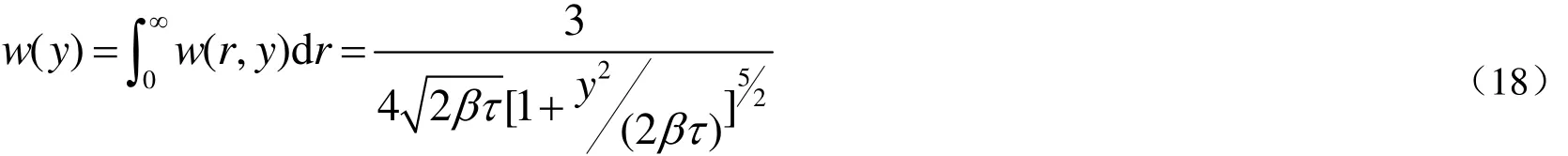
Soares等[17]利用单活性位的茂金属催化剂催化合成乙烯和辛烯共聚物用于验证Stockmayer分布。实验样品用升温淋洗分级技术（TREF）[18]和结晶分级技术（Crystaf）[19]进行组成分布的检测。

在表征共聚物的过程中，由于共聚物结晶的复杂性，Crystaf所测组成分布会比用Stockmayer模型预测的分布宽。由Wild的实验结果与模型计算得到[18]，直接由Stockmayer分布模型计算的分布较窄，实际所测的组成分布较宽。测试结果远不如GPC对分子量分布的测量精准。因此，共聚物组成分布的模型化研究仍然是一个任重道远的步骤，涉及共聚物组成的检测手段也需要更精确。

3 共聚物的序列分布

分子量分布和共聚物组成相同的共聚物，因其序列分布不同表现出不同的性质，如呈现出抗冲塑料的特性，也可以呈现出热塑性弹性体的特性等。

3.1 概率分析法

Ray等[4]提出用概率的方法来求出A和B两种单体的序列在整条大分子链中的分布。

假设两种单体分别为M1和M2，通过共聚的方式形成了如下一条聚合物链：～M2M2M2M1M1M1M2M2～。M1·和M2·分别代表了以单体M1和M2结尾的活性链。由M1生成M1M1和M1M2的概率分别为p11和p12，由M2生成M2M2和M2M1的概率分别为p22和p21，则有：

其中：r1和r2分别是两种单体的竞聚率。则形成n个A相连的概率为：A所以n个A相连的概率n是序列一个分布，称作序列分布。

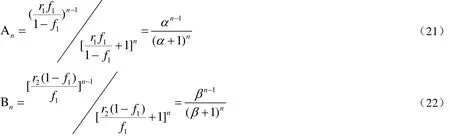
平均的序列长度：

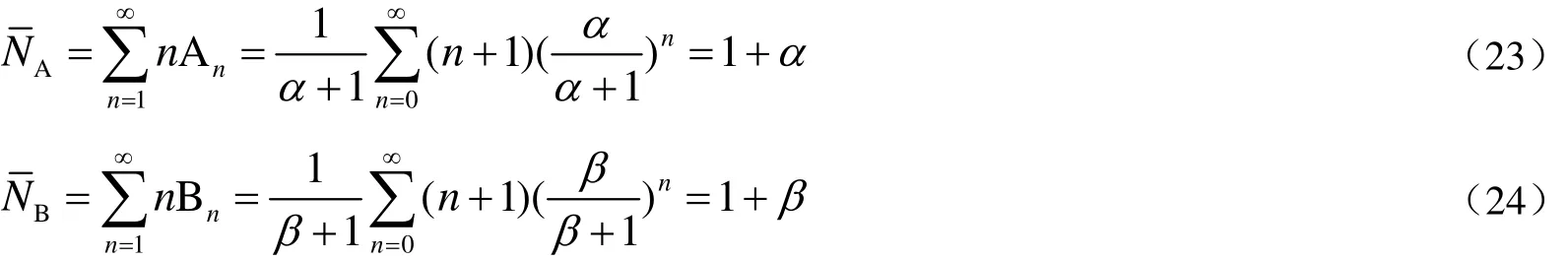
因此，知道参与反应单体的竞聚率和单体的瞬时浓度，就可以通过概率的方法求得单体在大分子链中的平均序列长度和分布。

Tosi等[20]在1968年就用概率法得到了在不同竞聚率下用单体百分比时序列长度分布表，求取了在一定的r1r2值下，不同共聚组成中不同长度的序列的分布。用概率分析法思路清晰，过程明确。缺点是概率分析法并没有针对实际的反应机理给出推导，并且要采用罗列的方法，计算量较大。

3.2 序列模型法

Ye等[21]仿照链结构的模型，写出了“序列模型”。该模型是指将原有的机理方程稍作改变，将链的生成转变为序列的生成。但是值得指出的是，序列模型只关注了序列的情况，其他的信息比如链长等都无法由序列模型得到，所以计算全链段的信息需要将“链模型”与“序列模型”结合起来求解[22]。该方法的思想为：该链在生成的过程中，以A结尾的活性链的序列为L，g为1，2，3……n。以B结尾的活性链序列为O。若一条链最开始是以A开始进行增长的，则记为L，接下来链再继续增长会有两种可能，继续与A相接或者接上B。当是第一种情况时，链的书写变为L，当是第二种情况时，记为O。以此类推。在这里写出链增长阶段的机理方程如表6所示。

表6 用序列模型表示链增长过程机理方程Table 6 The reaction mechanism of propagation using sequence model

Ye等[21]在使用这个模型时，实验采用苯乙烯和4-甲基苯乙烯分别在间歇和半间歇过程中进行可控自由基聚合。根据序列模型的概念，将原有的机理方程作了变换后，根据机理方程分别得到了d[L]/dt，d[L]/d t，d[O]/dt和d[O]/dt的表达式，再根据矩的定义（参照矩方法）通过以上式子得到A和B两种单体序列的零阶矩，一阶矩和二阶矩。在反应器中，物料守恒和体积变化的方程分别如下所示：

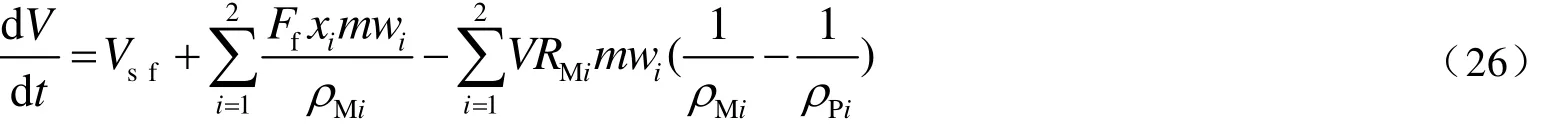
以上第一式中，V，Ci，Cif，Vf和Ri分别表示反应体系体积，物质i在反应器中的浓度、进料流股中物质i浓度、进料体积流量和物质i的反应速率。第二式中Vsf，Ff，xi，RMi，mwi，ρMi和ρPi分别表示溶剂的进料流率、总单体的摩尔流率、单体i的摩尔分率、单体i反应速率、单体i相对分子质量、单体i的密度和聚合物的密度。

单体的数均序列和重均序列分别可以由下式计算：

4 结 语

在以往的聚烯烃工业生产过程中，通过关联熔融指数来对聚合物的质量指标进行预测和控制，随着对产品质量要求的提高，面向聚合物链结构进行建模也得到了快速的发展。

矩方法可用于求解聚合物平均分子量以及分布指数，它提供了一种迅速简便的了解分子量的方法。Flory分布则提供了全面清晰的分子量分布信息，为了解聚合物分子量分布和动力学研究提供了充分的依据。这两种方法已逐渐取代熔融指数法成为工业生产中表征聚合物分子量及分布的重要依据。如何利用Flory分布对聚合物生产进行控制将会是未来科研工作进行的方向。

在对烯烃共聚物的研究中，共聚物组成及其分布提供了一个清晰的三维分布模型，将聚合物链结构的研究又往前推动了一步，通过数学建模可以得到共聚物的组成分布。但是，模型验证有一定的难度，这主要是检测仪器和模型本身不够完善引起的。因此，对共聚物组成模型的完善以及检测仪器的发展是今后研究工作的重点。

序列结构分布建模是分子量分布建模、共聚物组成建模的重要发展，能更清晰地描述聚烯烃的链结构特性，是烯烃聚合反应过程模型化领域的重要发展方向。序列模型法具有一定的参考意义，但还有非常多可供研究和发展的空间。对聚合反应机理深入和客观地认识，基于基元反应建立包含序列结构分布信息的烯烃聚合过程模型及其高效算法是面向链结构模型化的重点。

[1] Quackenbos H M. Practical use of intrinsic viscosity for polyethylenes[J]. Journal of Applied Polymer Science, 1969, 13(2): 341.

[2] Soares J B P, Hamielec A E. Kinetics of propylene polymerization with non-supported heterogeneous Ziegler-Natta catalysts effect of hydrogen on rate of polymerization ,stereoregularity, and molecular weight distribution[J]. Polymer,1996, 37(20): 4606-4616.

[3] Canu P. Discrete weighted residual methods applied to polymerization reactions[J]. Computer & Chemical Engineering, 1991, 8: 549-564.

[4] Ray W H. On the mathematical modeling of polymerization reactors[J]. Journal of Macromolecular Science-reviews in MacromolecularChemistry, 1972, C8: 1-56.

[5] Hamielec A E, MacGregor J F, Penlidis A. Multicomponent free-radical polymerization in batch, semi-batch and continuous reactors[J].Macromolecular Symposia,1987,10(11): 521-570.

[6] Soares J B P, Hamielec A E. Copolymerization of olefins in a series of continuous stirred-tank reactors using heterogeneous and supported metallocene catalyst I: general mathematical model[J]. Polymer Reaction Engineering, 1996, 4: 153-191.

[7] McAuley K B, MacGregor J F. A kinetic model for industrial gas-phase ethylene copolymerization[J]. AIChE Journal, 1990, 36:837-850.

[8] Flory P J. Principles of polymer chemistry[M]. Ithaca: Cornell University Press, 1953: 273.

[9] Soares J B P. An overview of important microstructural distributions for polyolefin analysis[J]. Macromolecular Symposia, 2007, 257(1):1-12.

[10] Soares J B P. Mathematical modelling of the microstructure of polyolefins made by coordination polymerization: a review[J]. Chemical Engineering Science, 2001, 7(56): 4131-4153.

[11] Soares J B P, Kim J D, Rempel G L. Analysis and control of the molecular weight and chemical composition distributions of polyolefins made with metallocene and Ziegler-Natta catalysts[J]. Industrial & Engineering Chemistry Research,1997, 36(4): 1144-1150.

[12] 顾雪萍, 冯连芳, 王嘉骏, 等. 乙烯淤浆聚合牌号过渡过程的模拟[J]. 中国科技论文在线, 2008, 3(12): 915-918.Gu Xueping, Feng Lianfang,Wang Jiajun. et al. Simulation for grade transition of ethylene slurry polymerization process[J].Science Paper Online, 2008, 3(12): 915-918.

[13] 顾雪萍, 王艳丽, 陈 曦, 等. 基于聚合物分子量分布的乙烯淤浆聚合工艺优化[J]. 化工学报, 2013, 64(2): 649-656.Gu Xueping,Wang Yanli,Chen Xi, et al. Optimization of ethylene slurry polymerization conditions based on molecular weight distribution[J]. CIESC Journal, 2013, 64(2): 649-656.

[14] Xie T, Hamielec A E. Modeling free-radical copolymerization kinetics-evaluation of the pseudo-kinetic rate constant method 1: molecular weight calculations for linear copolymers[J]. Macromolecular Theory and Simulations, 1993, 2(3): 421-454.

[15] 郑 耸. 基于反应机理的乙烯淤浆聚合流程重构的动态模拟和优化[D]. 杭州: 浙江大学, 2013.

[16] Alghyamah A, Soares J B P. Simultaneous deconvolution of the molecular weight and chemical composition distribution of polyolefins made with Ziegler-Natta catalyst[J]. Macromolecular Symposia , 2009, 285(1): 81-89.

[17] Soares J B P, Monrabal B, Nieto J, et al. Crystallization analysis fractionation(Crystaf) of poly(ethylene-co-octene)made with single-site-type catalysts: a mathematical model for the dependence of composition distribution on molecular weight[J]. Macromolecular Physical Chemistry, 1998, 199(9): 1917-1926.

[18] Wild L, Ryle T R, Knobeloch D C, et al. Determination of branching distributions in polyethylene and ethylene copolymers[J]. Journal of Polymer Science: Polymer Physics Edition, 1982, 20(3): 441-455.

[19] Hosoda S, Nomura H, Gotoh Y, et al. Degree of branch inclusion into the lamellar crystal for various ethylene/a-olefin copolymers[J].Polymer, 1990, 31(10): 1999-2005.

[20] Tosi C. Sequence distribution in copolymers: numerical tables[J]. Advan Polym Sci, 1968, (5): 451-462.

[21] Ye Y, Schork F J. Modeling of sequence length and distribution for the NM-CRP of styrene and 4-methylstyrene in batch and semi-batch reactors[J]. Macromolecular Reaction Engineering, 2010, 3(3-4): 197-209.

[22] Zargar A, Schork F J. Copolymer sequence distributions in controlled radical polymerization[J]. Macromolecular Reaction Engineering,2009, 3(2/3): 118-130.