基于Hu修正不变矩的商标识别
2014-03-28马亚琼朱颢东宫秋萍
黄 敏,马亚琼,朱颢东,宫秋萍
(郑州轻工业学院计算机与通信工程学院,郑州450002)
商标不仅便于消费者认牌购物,还可以为商家创立品牌,抢先占领市场,因此,商标识别在日常生活中有着重大意义和广泛的应用前景.目前,图像识别算法大多首先采用提取物体特征,然后再将待识别样本与模型进行匹配[1].商标图像特征一般包括颜色、形状以及版面等,与其它图像相比,商标图像的形状特征较颜色特征更为显著,因此一般采用形状特征进行识别.目前常用的图像形状特征提取算法主要有Fourier描述子、Hough变换、形状矩阵和矩不变量[2]等.其中矩特征以图像分布的各阶矩来描述灰度的统计特性,能较好地反映物体的形状信息,且具有较好的抗噪性能和稳定性.Hu[3]首先将矩用于形状识别,并提出了不变矩的概念.不变矩是一种比较经典的特征提取方法,它提取的是物体的全局特征,矩不变量不随物体的平移、旋转和缩放而改变,具有较好的不变性,因而被广泛应用在景物匹配、图像分析以及物体识别等许多方面[4].本文将Hu修正矩和最小距离分类器用于商标识别,仿真实验表明该方法不但满足不变矩的特征,而且还具有较高的识别率,可用于商标识别.
1 不变矩理论
已知二维连续图像函数f(x,y),则p+q阶原点矩定义为:

由于mpq不具有平移不变性,因此定义其相应的p+q阶中心距为:

对于数字图像,积分用求和来代替,mpq、upq分别由下面的式子表示:

当图像发生变化时,mpq会发生相应变化,upq虽具有平移不变性但依然对缩放和旋转敏感,定义f(x,y)的归一化p+q阶中心矩:
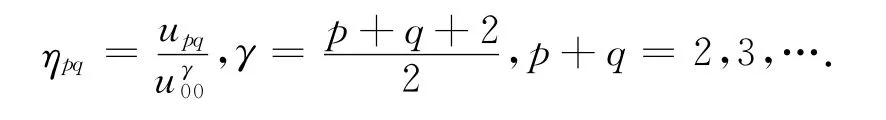
采用归一化中心矩进行特征表示,特征具有平移和比例不变性,但不具备旋转不变性.Hu利用它们的线性组合构造出了具有平移、旋转和比例不变的七个二维不变矩[5],其定义如下:


2 Hu修正矩
Hu提出的七个不变矩虽然在连续情况下满足平移、旋转和尺度不变特性,但在离散情况下,由于数字图像的比例变换造成图像的重采样与重量化,使得计算出的Hu矩不能准确的反映原目标的特征,造成原目标一些信息的丢失.文献[6]对七个不变矩作了修正,由于不变矩的变化范围很大,为便于比较,采用取对数的方法进行数据压缩;同时考虑到不变矩可能出现负值的情况,在取对数之前先取绝对值,实际采用的不变矩为:

然后,构造新的不变矩φ″1~φ″7,使其在离散情况下具有比例不变性,具体公式如下:

3 基于Hu修正不变矩的商标识别
基于修正不变矩和最小距离分类器方法的商标识别系统主要包括图像采集、商标图像预处理、特征提取和特征匹配几个部分.其中特征提取是预处理和特征匹配之间的桥梁,选择能充分反映目标基本形状和属性的特征,是目标图像识别的一个重要环节.
3.1 商标图像的预处理
为提高商标识别的精确度以及准确性,需对待识别的图像进行预处理.图像的格式有很多种,为了提取特征,必须将图像进行归一化处理,如尺度归一、灰度处理、格式转换、噪声滤除及二值化处理等.尺度归一将图像统一成为一个尺寸的大小;格式转换可在系统中采用专用控件处理或采用工具软件提前处理;噪声滤除为使提取的特征不受噪声的影响.合理的预处理能提高图像的处理速度,降低算法的复杂度.
3.2 基于最小距离分类器的特征匹配
本文采用最小距离分类器方法来进行特征匹配.最小距离分类器[7]是一种简单的线性分类方法:设有c类已知类别的模式样本,它们的均值分别为m1,m2,…,mc,定义判别函数如下:

按最小距离分类原理的决策规则为:
若di(x)<dj(x) (j=1,2,…,c;j≠i),则x∈ωi.
上式可改写为:

去掉与i无关的项,则为:

由此,决策规则变为:
若di(x)>dj(x) (j=1,2,…,c;j≠i),则x∈ωi.
3.3 商标识别过程及分析
商标识别的步骤[8]为:先对一些标准商标图像进行人工分类,本文以图1中3个商标为例.

图1 三个标准商标图像Fig.1 Three standard trademark images
分别对各商标图像进行平移、旋转和尺度变换操作,计算变换后图像的修正矩特征值,求出同一类图像的特征向量的平均值,该值即代表此类图像的特征向量,并组成此类商标的数据库,用同样的方法得到其它商标的数据库,以便于进行目标识别.当判断待识别目标属于哪类商标时,只需求该目标与已知各商标的最小距离,并将待识别目标归为使得计算结果最小的那类中.
(a)求标准图像的特征向量
在Matlab编程环境下对原图像进行预处理,再对处理后的图像进行平移、旋转和缩放操作,求出各图像的修正矩特征值,以图(1)中(a)的旋转和缩放操作为例,所得结果如表1和表2所示.

表1 旋转图像的Hu修正矩值Tab.1 Hu modified moment values of rotated images(°)

表2 缩放图像的Hu修正矩值Tab.2 Hu modified moment values of scaled images
为便于比较,计算各操作相应的Hu矩特征值,如表3和表4所示.

表3 旋转图像的Hu矩值Tab.3 Hu moment values of rotated images(°)

表4 缩放图像的Hu矩值Tab.4 Hu moment values of scaled images
由表1和表2可知,不同操作下的同类图像对应的修正矩值基本不变,证明了该修正矩具有旋转和尺度不变特性.从表3和表4可以看到,求得的Hu矩值不但出现了负值而且数值普遍较小不利于表达;且同类图像经过不同操作得到的特征值差别也相对较大.可通过计算以上各表格的平均相对误差来进一步比较Hu修正矩和Hu矩,结果如以图2和图3所示.

图2 旋转图像平均相对误差Fig.2 Mean relative error of rotated images

图3 缩放图像平均相对误差Fig.3 Mean relative error of scaled images
从图中可以看到,Hu修正矩的平均相对误差比Hu矩的小的多,证明了Hu修正矩的优点,可用于商标识别.然后以同样的方法求图(1)中(b)和(c)各操作对应的Hu修正矩值,再将同类图像中各幅图像的特征值求平均,得到一个表示该类图像的特征向量.
(b)待识别图像的特征匹配
待识别图像如图4所示.

图4 待识别图像Fig.4 The identified image
对待识别图像进行预处理操作,并计算处理后图像的修正矩值,如表5所示.

表5 待识别图像的特征值Tab.5 Feature values of the identified image
为进一步验证该修正矩的可行性,按以上方法分别用Hu矩和Hu修正矩对30幅商标图像进行识别,在测试样本数目相同的情况下,Hu不变矩的识别率为86.67%,而修正Hu矩的识别率高达93.33%,相对Hu矩有所提高.
4 结束语
本文介绍了一种基于Hu修正矩的特征提取算法,并将其应用在商标识别中.实验结果表明图像无论是旋转、缩放还是平移,其修正矩值都基本保持不变,具有良好的稳定性.同时通过实验对比可知该修正矩比原始Hu矩具有更高的识别率,可推广应用到其他图像识别领域.
[1] Yuma,A,Shafique K,Shah M.Target tracking in air borne forward looking infrared imagery[J].Image Vision Compute,2003,21(1):623-635.
[2] Doermann D S,Rivlin E,Weiss I.Logo Recognition Using Geometric Invariants[C]//Proceedings of the 2nd International Conference on Document Analysis and Recognition.USA:IEEE,1993:206-217.
[3] 魏伟波,芮筱亭.不变矩方法研究[J].火力与指挥控制,2007,32(11):114-117.
[4] 张 蕾,刘 勇,范庆辉.基于修正不变矩和范数的物体特征识别方法[J].微电子学与计算机,2008,25(6):42-45.
[5] Hu M K.Visual pattern recognition by moment invariants[J].IRE Transactions on Information Theory,1962,8(2):179-187.
[6] 于 红,王金伟.基于改进的Hu不变矩的电力图元特征提取[J].沈阳工程学院学报:自然科学版,2009,5(1):53-55.
[7] Jain A K,Duin R P W,Mao J C.Statistical pattern recognition:a review[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(1):4-37.
[8] 商立群,杜亚娟.Hu矩和Zernike矩在图象识别中的应用[J].西安科技学院学报,2000,20(1):53-56.
