我国住房价格未来走向模拟与调控——基于人口结构和城镇化长周期视角<br/>

我国住房价格未来走向模拟与调控——基于人口结构和城镇化长周期视角

2014-03-28孙洁雅王树强

河北经贸大学学报(综合版) 2014年3期

叶莉，孙洁雅，王树强

（河北工业大学经济管理学院，天津 300130）

一、引言

近年来，我国人口结构的变迁、城镇化进程的加快，一定程度上加剧了住房市场的供需矛盾，致使住房价格出现了新一轮的非理性上涨。但自2014年初，我国住房价格“高歌猛进”的增长态势悄然消失，一些城市的住房价格出现了松动，“住房市场是否会崩盘”引发了众多行业领袖和专家学者的激烈争论。据现有国际经验，投资和投机性需求自然是房价上扬的重要原因，但若忽视住房价格的根源性推动力——人口结构和城镇化，那么这种非理性繁荣往往预示着衰退、萧条的到来。以日本、美国为例，20世纪80年代日本地产市场出现泡沫，住房价格在1986—1989年翻了两番，但因其未能及时消弭老龄化社会带来的巨大压力，90年代末住房市场出现了大崩溃；而20世纪70年代，美国20～30岁购房主力军人口比重激增，推动房价上涨了近30%，但十余年后住房需求开始下跌，市场出现低迷，美国通过建立房利美及房地美、推行可调整的抵押贷款利率等金融手段，虽然缓解了人口结构变迁压力，但同时也为2008年的金融危机埋下了伏笔。因此，为避免我国住房市场重蹈美、日覆辙，需在不过于依赖金融政策的前提下未雨绸缪，这势必要从推动住房价格的根源——人口结构和城镇化着手。而准确预测住房价格出现重要转折的时间点，有助于政府依照住房市场的发展趋势，更加细致地设计调控政策，更加精确地制定政策实施的时间及力度，确保住房市场的长期稳定。

Mankiw和Weil（1989）[1]采用近似索罗模型的平衡增长路径分析法，证明了人口结构是美国20世纪70年代住房价格上涨的主要原因，且人口结构对住房价格的推动力会逐渐减弱，将于20年后消失，住房价格自此开始下跌；McFadden（1994）[2]通过延长时间序列数据对Mankin的研究做了进一步分析，结果显示美国住房价格将于21世纪初陡降。Fumio Ohtake（1996）[3]和 Gabriels.Lee（2001）[4]采用相同的研究方法分别对日本和奥地利的人口结构和住房价格进行了分析，均得到了相同的研究结果。可见，众多发达国家的住房价格上涨均与人口结构变迁密切相关，但就目前几个新兴经济体发展现状来看，刘颖春（2004）[5]、Ramesh Kumar（2011）[6]、骆永民（2011）[7]和邓翔（2013）[8]等人发现人口结构并不是住房价格的唯一推动力，城镇化也可通过刺激住房需求进而推动住房价格上涨。由此，部分学者从人口结构、城镇化视角对住房价格进行了研究：李雄军（2011）[9]通过汇总和分析1980—2010年相关数据发现，人口结构不仅与城镇化有联系，对住房价格也有一定的推动力。哈继铭（2007）[10]认为我国住房价格受人口结构和城镇化双核驱动，并预计自2015年开始人口结构这一引擎将逐渐熄火，城镇化马力也将减弱，住房价格增速将会减慢；而杨静（2012）[11]预测我国将于2027年进入老龄化社会，2023年进入城镇化后期，在需求最大化的理想状态下房地产还有10年的发展期。

由以上学者的研究成果可知，基于人口结构和城镇化视角模拟房价的未来走势具有重大的理论价值和实际意义。但众多学者从人口结构和城镇化视角讨论住房价格走势，其结果相差较大，且仅停留在定性分析上。此外，学者们在研究人口结构、城镇化对住房价格的影响时，均将人口结构和城镇化默认为互不影响，但实际上，人口结构和城镇化紧密相关，人口结构不同，城镇化发展水平和速度也会不同（Yasuhiro Sato，2004[12]；张立，2009[13]）。鉴于此，本文通过实证检验挖掘人口结构与城镇化的关系，确定二者对住房价格的影响；再构建含有城镇人口增速的Poterba模型，预测人口结构和城镇化推动力减弱和消失的时间点，从而模拟住房价格未来走势；最后确定人口结构和城镇化对住房价格的影响程度，从户籍制度、二胎政策和城镇化速度三方面对如何保证住房市场健康平稳发展进行讨论。

二、人口结构、城镇化与住房价格间关系：实证检验

（一）指标界定与数据说明

人口结构包括人口自然结构、人口社会结构、人口地域结构和人口经济结构。其中，人口自然结构包括年龄结构、性别比；人口社会结构包括家庭规模、人口收入结构和人口文化结构；人口地域结构包括非农人口比重、人口净迁移率；人口经济结构包括从业人员产业结构和从业人员职业结构。已有研究结果显示，全国人口净迁移率、从业人员职业结构、家庭规模和收入结构对城镇化和房价呈弱势影响[14]，且前两个指标的统计困难、准确率较低。

鉴于此，秉着可得性、代表性和权威性原则，指标设定如下：X1为总人口年增加量；X2为14岁～64岁人口比重，即劳动力人口比重，代表人口年龄结构；X3为非农人口比重，代表拥有城市户籍人口占总人口的比重；X4为第三产业从业人员人口比重；X5为6岁及6岁以上人口的人均受教育年限；X6为人均国民生产总值，该指标为除人口结构外影响住房价格的其他因素的代表性指标；Y为城镇人口与总人口之比，代表城镇化率；P为商品房平均销售价格，由商品房销售额除商品房销售面积得到，代表住房价格。为了增加数据的平稳性，消除回归方程的异方差，避免时间序列数据普遍具有的趋势性，将各指标分别取对数。

本文选取1982—2011年数据，其中X1、X2、X3、X4和X5来源于2007—2011年《中国就业和人口统计年鉴》及1998—2006年《中国人口统计年鉴》，X6和Y源于《2012年中国统计年鉴》。其中，1983—1985、1989、1992年的劳动力人口比重为缺省值，根据该指标总体发展趋势对数据进行了补充。

（二）格兰杰因果检验结果

首先，采用ADF单位根检验法对以上8个变量进行稳定性检验，结果显示各变量均为一阶单整序列。根据AIC准则确定滞后阶数，进行格兰杰因果检验。结果如下：第一，城镇化是住房价格的格兰杰原因，住房价格亦是城镇化的格兰杰原因；第二，人口年龄结构、非农人口比重、总人口年增加量和人均国民生产总值是城镇化发展的直接原因；第三，人均受教育年限和第三产业从业人员比重通过总人口年增加量影响城镇化的发展，为城镇化发展的间接原因；第四，人口结构各因素和人均国民生产总值均不是住房价格上涨的直接原因，通过城镇化影响住房价格。可见，城镇化进程加快刺激了住房价格上涨，而城镇化进程加快又是由人口结构变迁引起的。由此，城镇化是住房价格的直接推动力，而人口结构是住房价格的根本性原动力，且以城镇化为媒介影响住房价格。

基于以上研究发现，以人口结构、城镇化为切入点，可完美解释2003—2013年住房价格为何会持续性上扬。从人口结构现状来看：第一，作为由农村移居城市的主力军，14岁～64岁人口比重逐年上升，于2010年达到顶峰，为74.53%，即10人中就有7.5人为劳动力人口；第二，我国人均受教育年限逐年提升，高校毕业生数量越来越多，仅2013年高校毕业生就有近700万人，且大多选择留在城市而不是返乡；第三，第二、三产业的发展大大提升了城镇吸纳外来人口的能力，数亿农村剩余劳动力开始转向城镇寻求工作机会。人口结构的优势，再加之政府的支持和鼓励，为城镇化提供了绝佳的发展机遇，自1995年城镇化进程开始加快，城镇化率年均增加近1.4%。城镇新增人口自然会产生住房刚性需求，同时改善性需求也在增多，加之住房供给的时滞性，多重压力造成住房供给严重失衡，住房价格开始上扬。继而，在利益驱动机制的作用下，热钱不断流入房地产业，建筑材料和土地资源也随之涨价，致使住房价格继续增高，形成恶性循环，造成住房价格持续非理性上涨。可见，若人口结构变迁和城镇化进程对房价的根源性推动力消失，投资和投机性需求对房价的推行也只能是外强中干，房地产业的繁荣期也就持续不了多长时间，因此基于人口结构和城镇化讨论和预测房价的未来走势更具准确性和科学性。

三、Poterba模型的构建与估算

（一）Poterba理论模型

1.模型基本假定条件

采用本模型预测住房价格，需满足四个假设条件：（1）经济具有中长期均衡的特征。即住房市场竞争完备，从中长期来看，市场处于均衡状态，且供给等于需求，从而市场能够出清；消费者和企业之间的信息完全对称，两者基于理性预期作出决策。（2）住房都是同质的。假设全国住房市场的住房存量为Q（t），在短期内住房存量保持不变；住房的实际价格为 P（Q），且 P（Q）＜0。（3）假设住房的需求量为Qd=f（R）N，且f′（R）＜0，其中R为每平方米的住房租金，N为城镇人口总量；住房的供给量为QS，达到均衡的条件为Qd=QS=Q，即f（R）=Q/N。（4）令q=Q/N，则q为城镇居民人均住房面积，市场出清时的每平方米的租金为 R=R（q），理论上 R′（q）小于零，但从我国的现实情况来看随着人均住房面积的增加，住房价格不断攀升，住房租金也在不断上涨，因此，R′（q）＞0。

2.构建含有城镇人口增速的Poterba动态均衡模型

（1）住房价格的变动方程

设住房的折旧率为δ，住房的维修费率为k，房产税为μ，社会平均资本收益率为γ（金融机构一年期存款利率），则投资者不致亏损的必要收益率为w=δ+k+μ+γ，只有在购买住房的边际收益大于等于边际成本，即wp≥R（q）的情况下，消费者才具有购房的动机。住房的实际价格变动值等于投资者的必要收益减去住房的租金收入，即：

（2）住房存量的变动方程

住房的折旧率为δ，则住房存量的折旧量为δQ；设φN为城镇竣工住宅建筑面积①，表示住房市场的供给量，供给由住房的实际价格决定，即φ=φ（P），并满足φ′（P）＞0，则在考虑城镇化水平的条件下，住房存量的变动方程为：

由 q=Q/N 得，q˙=（Q˙N-Q˙N˙）/N2，再令城镇人口的年增长率为 n，n=N˙/N，则q˙=Q˙/N-nQ/N，将（2）式两边均除以 N，变为Q˙/N+δQ/N=φ（P），带入（2）式，住房存量变动率的变动方程：

（3）Poterba动态方程组

将住房价格和住房存量变动方程联立，构建含有城镇人口增速的Poterba动态方程组：

为简化Poterba模型的估算过程，本文借鉴J.M.Poterba[15][16]的研究成果，假设 R（q）和 φ（P）两个函数中分别只有q和p一个自变量，且均为自变量的幂函数，即 R（q）=b1qb2，φ（P）=a1Pa2。简化的 Poterba 动态方程组为：

方程组（5）用数学表达式形象地表述了住房市场相关变量之间的关系。从短期来看，住房存量变化率q和住房的实际价格P是固定不变的，即q˙=0，P˙Q=0，得到含有城镇人口增速的住房存量与价格动态变化的局部均衡模型:

该式可用于对R（q）和φ（P）函数的估算。

3.Poterba模型计算方法

该模型利用两点边值问题和多重打靶法两种数学思想，对住房价格（P）未来走势进行求解。动态经济系统的两点边值问题可用如下表达式表达：

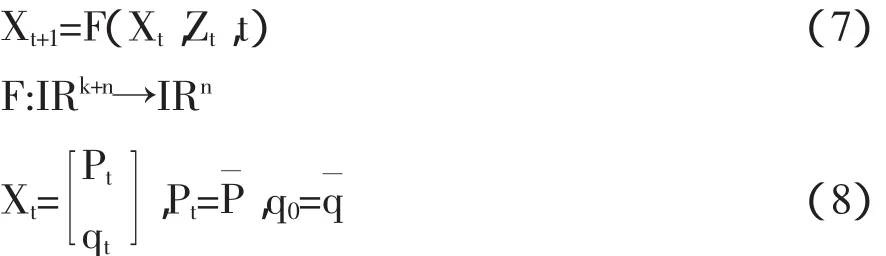
其中，P为住房价格，q为城镇人均住宅面积，Z代表影响住房价格的其他全部影响因素。Xt为n×1维列矩阵，Zt为k×1维列矩阵；Pt为m×1维列矩阵，qt为（n-m）×1为列矩阵。

（8）式为（7）式所满足的边值条件。由（7）式可知，Xt是Xt-1的函数，Xt-1是Xt-2的函数，逐步递推可得，Xt是关于X0的函数，即可将（7）式变为Xt=H［X0；｛Zi｝i=0，t］。最终目的是为了找出P0=P*，使其满足以下条件：

令Hm为H的前m个方程，则有Pt=Hm（X0；｛Z｝ii=0，）t=Hm］；｛Z｝ii=0，t），利用一级泰勒公式将其展开，展开式为：

若Hm为线性函数，（11）式是与事实完全相符的，得到的是精确的结果；若Hm为非线性函数，得到结果为近似值。若Hm为非线性函数，可根据多重打靶法，将［0，T］区间分为 N 等份，即［0，T1］，［T1，T2］，...，［TN-1，TN］，TN=T，由于 N 足够大，可将任一区间［Ti-1，Ti］内的曲线近似看为直线，则有:

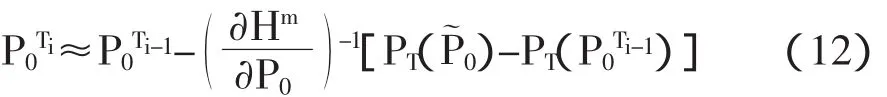
（二）模型估计

住房市场不同，函数 R（q）、φ（P）、w、δ 等参数会有很大的区别。为提高结果的准确性，本文结合相关文献和我国住房市场实际情况，对w、δ进行假设。鉴于1987年以前，城镇居民住房价格低于市场价格，故本文选取1987—2012年数据，利用线性回归对R（q）和φ（P）进行估算，得出符合我国住房市场特色的Poterba动态模型。

1.模型相关系数假设及 R（q）、φ（P）函数估算

校准邹至庄（2011）[17]等人的研究结果，以简捷为原则，利用最小二乘法进行线性回归，估算R（q）和 φ（P）两个函数。

（1）估算 R（q）函数

假设折旧率δ=0.02，维修费率k=0.03，社会平均资产收益率γ=0.032，房产税已在上海等几个大城市试点，未来全面征收房产税是大势所趋，在此以上海为基准，其税率为0.4%～0.6%，取中间值，令μ=0.005，则 w=0.087。可将 R（q）=wp 写为：

其中，log（p）=β0＋β1log（q）-log（w）＋ε=β0＋β1log（q）＋ε1，显然，β1为住房需求价格弹性的倒数。选取 1987—2012 年数据，log（wp）为因变量、log（q）为自变量，利用最小二乘法进行一元回归，回归结果为：

（2）估算 φ（P）函数

选取1987—2012年数据，以城镇竣工住宅建筑面积/城镇人口，即φ（P）为因变量，商品房平均销售价格（p）为自变量，分别取对数表示为 lnφ、lnp，回归结果为：

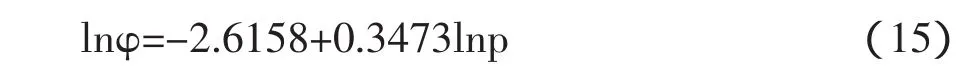
2.模型估算结果

根据R（q）和φ（P）的估算结果，将相应的计算结果和假设系数代入（5）式，得到与我国住房市场实际情况相符并融合城镇人口增速的Poterba动态方程组：

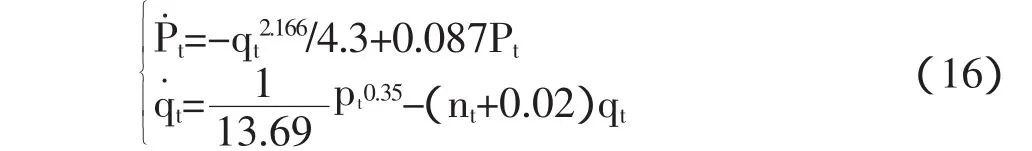
其中，nt为第t年份城镇人口增速；Pt为t年份住房价格，qt为 t年份城镇居民人均居住面积；P˙t、q˙t为第 t年份 R（q）和 φ（P）函数的导数。

由估算过程可知，Poterba模型存在以下不足：一是，（16）式中 R（q）和 φ（P）中的常系数以及 w、δ和n均为估算值，且没有实现动态化，精确率较差；二是，模型中R（q）的导数为正值，代表着住房需求价格弹性为正值。上述两方面问题决定了住房价格模拟结果上涨幅度偏小，下降幅度偏大，住房价格具体数值失真。鉴于本文关注点为住房价格变动的时间点而不是其变动过程，因此上述问题并不影响本文的研究。

方程组（16）式中P˙t、q˙t为内生变量，nt为外生变量。换句话说，城镇人口增速（nt）决定着房价的变动幅度（P˙t）。结果表明：一方面，随着人口结构对城镇化的推动力逐渐减弱及城镇化进程的不断加深，城镇化速度会逐渐减缓；另一方面，1987年伊始，人口总量逐年下跌，2027年之后将转为负增长。城镇化速度的降低和人口总量下降两方面因素决定了城镇人口增速必然会逐渐降低。由此可推，随着人口结构的变迁和城镇化的发展，住房价格终将下跌。而房价具体将于何时转为负增长，还需进一步估算。

四、模拟住房价格未来走势

（一）预测城镇人口变化趋势，求解nt

1979年，诺姆瑟发现城镇化发展全过程可以近似为一条被稍微拉平的S型曲线，称为“诺姆瑟”曲线，具有阶段性规律。本文通过模拟S型曲线预测2012—2050年城镇化率。假设y为城镇化率，t为时间，a、b为常数，则城镇化发展历程可用以下方程式表示。

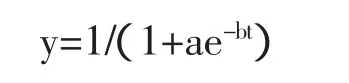
两边取对数，则有：

令 y1=ln（1/y-1），β0=lna，β1=-b，（17）式变为 y1=β0+β1t。鉴于我国城镇化自1978年才开始平稳增长，本文选取1978—2011年数据，令1978年t=0，1979 年 t=1，......，2011 年 t=33。根据 y求 y1，利用最小二乘法进行回归，得到如下结果：

由（18）式可得，α=eβ0=4.664 59，b=-β1=0.047，从而城镇化水平的时间序列方程式为：

根据（19）式，预测2012—2050年城镇化率，结果如表1所示。

表1 2009—2050年中国城镇化水平和增长率（%）

利用PANIS-INT人口软件预测2012—2050年人口情况，具体来说，以2011年人口年龄结构为起始数据，假设总和生育率年均增长0.02，从2011年的1.3上升至2050年的2.10②，女性预期寿命从77岁升至2050年的81岁，男性预期寿命从72岁升至77岁。将所得2012—2050年人口总量预测数据与城镇化率相乘，结果显示，城镇人口增长率与城镇化率增长率变动情况基本相同。再加之人口结构对住房价格的推动力会先于城镇化减弱和消失（哈继铭，2007），为使之后的讨论更加准确、便捷，本文用城镇化率的增长率替代城镇人口增长率，即2009年n为0.029，2010 年为 0.032，……，2050 年为0.007。

（二）住房价格走势模拟结果及分析

由Poterba模型计算方法可知，采用该模型预测住房价格，涉及40余次迭代，计算过程复杂、出错率高。为确保在短时间内得到高度准确的计算结果，本文以2009年的住房价格（P）和城镇居民人均居住面积（q）为初始值，利用C++语言编程，进行41次循环。如图1所示，自2014年开始，我国宏观经济减速换档，住房市场供求矛盾逐渐缓和，住房价格增速放缓；2021年之后，住房市场进入调整期，该阶段住房价格有两种可能，一是名义住房价格不变，但因通货膨胀实际住房价格缓慢下滑；二是名义和实际住房价格均开始下滑。

根据模拟结果，可将住房价格未来走势划分为三个阶段：第一阶段，2003—2013年，人口结构、城镇化保持较强的推动力，住房价格增速持续上扬。第二阶段，2014—2021年，随着人口增量和劳动力人口比重的降低，人口结构、城镇化的推动力减弱，住房价格增速开始下降，保持缓慢温和的增长态势。第三阶段，2022—2050年，由PADIS-INT软件预测结果可知，2022年之后我国人口增长速度基本为零，劳动力人口比重于2022年左右降至70%以下，总抚养比增至40%以上，城镇的生活成本愈来愈高，城镇化发展速度减缓，人口结构和城镇化对住房价格的推动力消失。

可见，在现有人口结构演变路径和城镇化发展趋势下，住房市场的繁荣至多再维持七年左右，若政府对住房价格的调控力度未能及时放松，致使住房价格提前下跌，其寿命可能会更短。住房市场凭借其高强度的产业关联度，稳居我国经济的支柱型地位，一旦住房价格下跌，如同多米诺骨牌，开发商失去信心，购房者因价格预期效应停止购房，住房市场及其相关产业出现颓势，那么我国经济必将出现动荡甚至萧条。就当前的实际情况来看，用七年的时间改变住房市场的经济地位是远远不够的。因此，若要保证我国经济持续健康发展，住房市场的长期调控核心是：在防止住房价格反弹的同时，尽量延迟价格下跌的时间点，延长住房市场寿命，为经济结构转型争取更多的时间。

图1 2010—2030年我国住房价格模拟结果

五、住房价格模拟结果的影响路径和调控策略

考虑到人口结构主要以城镇化为媒介推动住房价格，本文首先采用线性回归确定人口结构各因素对城镇化的影响程度，再以调整Poterba模型的相关变量为手段，探究人口结构和城镇化对住房价格的影响程度，进而分阶段提出调控策略。

（一）确定人口结构各因素对城镇化的影响程度

为避免出现多重共线性，本文以lnY为因变量，lnX1、lnX2、lnX3、lnX4 和 lnX5 为自变量，采用逐步回归法筛选自变量，后剔除lnX4和lnX5两个自变量。回归模型如下：

结果显示F=1 594.973，检验值很大，回归方程的整体是显著的；R2=0.994 596，说明回归方程的拟合程度很好；t检验结果表明四个解释变量对lnurbanrate影响都很显著。再对该回归方程进行LM和white检验，检验结果显示该回归方程不存在自相关和异方差。据回归结果所得弹性系数可知，劳动力人口比重对城镇化影响最大，非农人口比重次之，人口增量影响最小。而人均受教育年限和第三产业从业人员比重对城镇化没有直接影响，可认为其对住房价格的影响较小。因此不讨论对二者对住房价格的影响。

（二）探究人口结构与城镇化对住房价格的影响程度

1.城镇化对住房价格的影响最为显著，且效果显现速度最快。城镇化对住房价格具有显著正向影响，可直接调节模型中的nt估测其对住房价格的影响程度。由图2可知，若城镇化速度增加0.1%，即nt′=nt+0.001（t=0，1，…，42），住房价格于 2024 年左右转为负增长；若增加 0.2%，即 nt′=nt+0.002（t=0，1，…，42），住房价格于2027年转为负增长。可见，城镇化对住房价格的影响显著，且因其直接影响住房价格，调整效果可很快显现。

图2 2011—2030年不同城镇化增速下住房价格增值

2.非农人口比重对住房价格的影响较大，效果显现速度仅次于城镇化。回归结果显示，非农人口比重对城镇化率的弹性系数为0.189，可近似为非农人口比重增速每增加1%，城镇化增速就会增加0.189%③。按此比例可知，若非农人口比重增速增加0.5%，则城镇化速度增加0.099%，近似为0.1%，由上文分析结果可知，住房价格将于2024年转为负增长（见图2）；若非农人口比重增速增加1%，则城镇化速度增加0.198%，近似为0.2%，住房价格于2027年转为负增长。可见，以城镇化为途径，非农人口比重对住房价格影响显著。而户籍制度是调控非农人口比重的关键，因此可将该制度的改革作为调控住房价格的重要手段。

3.劳动力人口比重对第三阶段的住房价格有一定的影响，人口总量对住房价格影响甚微。回归结果显示，劳动力人口比重（X2）对城镇化的影响最大，人口增量（X1）次之。理论上说，二者对促进城镇化速度进而调控住房价格效果最佳，实际上人口政策具有较强的时滞性，因此若以实行单独二胎或二胎政策为手段提高人口总量和劳动力人口比重，对“延长住房市场寿命”效果甚微④。但劳动力人口比重凭借其对城镇化的强劲影响力，对减缓住房价格下跌趋势效果甚佳。假设2030年后劳动人口比重年降幅减少0.1%，城镇化速度增加0.19%，即nt1=nt+0.001 9（t=20，31，…，42），则住房价格降幅年均减少2%；若其下降幅度每年减少0.2%，城镇化速度增加0.38%，住房价格降幅年均减少3%。可见，以提高劳动力人口比重为手段可有效缓解2030年后的住房市场困境。值得注意的是，随着非农人口比重降幅的增加，对住房价格的影响效果会逐渐减少，以帕累托最优为原则，2030年之后，劳动力人口比重增速的增量应控制在0.2%之内，城镇化速度控制在nt+0.4%之内。

（三）调整人口结构和城镇化发展路径，重塑住房价格未来走势

基于以上研究可知，从长远来看，应把人口结构和城镇化作为重点调控手段，并辅以其他调控政策，标本兼治，从而实现住房市场缓慢温和的增长态势。2014年之后，人口结构和城镇化的推动力减弱，住房价格增速下滑，该阶段主要有两项紧要任务：尽量延长住房市场寿命和提前为住房价格将转为负增长做准备。一方面，应逐步放开抑制房价的调控政策，同时适度加大户籍制度改革力度，减小非农人口比重下跌幅度，加快城镇化步伐（上文分析可知速度增加幅度控制在0.2%左右），增加住房需求，可将住房价格负增长转折点延长至2027年左右。另一方面，十八届三中全会提出的“单独二胎”政策会引起人口结构的变动，有利于缓解第三阶段住房价格下滑困境，实现缓慢温和的增长态势。

六、主要结论

本文在确定人口结构、城镇化和住房价格三者间关系的基础上，建立了含有城镇人口增速的Poterba动态均衡模型，从人口结构和城镇化视角，对我国住房价格的未来走向进行了预测，并运用该模型对如何优化模拟结果进行了探讨。基于本文研究，可以得出以下结论：

1.我国新一轮的住房价格非理性上涨为双核驱动，其中城镇化为直接推动力，人口结构以城镇化为媒介对其产生影响，为根本性原动力，且二者的推动力会逐渐减弱直至消失。就当前我国住房市场现状来看，人口结构和城镇化对住房价格的推动力减弱萌芽初现，并将于2021年左右消失，即在现有人口结构和城镇化的发展趋势下，我国住房价格在短期内不会出现暴跌或暴涨的情况，而是将维持一段时间（七年左右）的缓慢温和增长态势，之后进入调整期。

2.户籍制度改革的力度和时间对住房价格存在着不可忽视的影响力。户籍制度为调控非农人口比重增速的主要手段，其改革实施的时间决定了非农人口比重增速将于何时提高，改革力度决定了其增速提高的程度。而非农人口比重可以城镇化为媒介，影响住房价格未来发展趋势。由此，户籍制度可通过调控非农人口比重影响住房价格。

3.因人口政策具有时滞性，“单独二胎”政策仅能通过改变劳动力人口比重增速对2030年之后的住房价格产生影响，可缓解城镇化减速和住房价格下滑时期的困境。由此，全面推行单独二胎政策时，不必顾虑对其住房市场的影响，仅考虑人口基数问题即可。

4.人口结构和城镇化对抑制当下住房价格攀升速度的效果甚微，但从长期来看，若主动、合理、恰当地调整二者的发展趋势，适当辅以调整贷款利率等调控政策，可有效延长住房市场寿命，将其负增长转折时间点推迟至2027年，同时还可缓解第三阶段住房价格下滑的经济困境。也即表明，从长远来看，为实现住房市场可持续健康发展，需从人口结构和城镇化着手。

需要说明的是，本文的研究方法还可以从以下两个方面进行改进：一是Poterba模型预测的住房价格与实际值有较大的偏差，可借鉴其他发达国家发展经验，将折旧率、维修率等指标动态化，减少偏差；二是人口结构、城镇化和住房价格都具有强烈的地域性特点，而且城镇化对住房价格的推动力与城市的经济发展水平和城镇化水平有关，可进一步根据各地区的实际发展特点，分区域对该问题进行研究，更具针对性。

注释：

①住宅市场具有城镇区域属性，鉴于此，本文只考虑城镇住宅的竣工面积。

②我国统计数据显示，2011年的总和生育率为1.18，由于存在漏报、错报等情况，导致结果数据偏低，鉴于此，本文将2011年总和生育率假设为1.3。而维持一个国家和地区人口规模长期稳定所需要的平均每个妇女生育2.1个孩子，十八届三中全会提出的单独二胎政策意味着我国总和生育率将有一定的提升，本文假设其每年上涨0.02，则我国将于2050年恢复至稳定水平，即2.1。

③lny=β0+β1lnx式中 β1≈，因此可近似认为x增速每增加1%，y的增速增加β1。

④假设2015年开始全国范围施行单独二胎，用3年左右改变部分大城市居民的生育观念，2018年出现婴儿潮，人口总量降幅开始下降，人口负增长可延迟3～5年。但在2032年之前，由于人口总量的降幅减小，劳动力人口比重会加速下降，直到婴儿潮时期出生的婴儿成长为劳动力人口之后，即2032年，劳动力人口比重开始迅速上涨。2032年之前，总人口对城镇化的推动力增加，劳动力人口比重的推动力减弱，两者相抵，可近似认为城镇化增速保持不变，由此对2032年之前的住房价格几乎没有影响。

［1］Mankiw N.G ，Weil D.N.The Baby Boom，the Baby Bust and the Housing Market［J］.Regional Science and Urban Economics，1989，（19）：235-258.

［2］McFadden D.Demographics，the Housing Market，and the Welfare of the Elderly［M］.National Bureau of Economic Research，1987.

［3］Fumio Ohtake，Mototsugu Shintani.The Effect of Demographics on the Japanese Housing Market［J］.Regional Science and Urban Economics，1996，（26）：189-201.

［4］Gabriels.Lee.Austian Demograghy and Housing Demand：Is The a Connection［J］.Empirica，2011：259-276.

［5］刘颖春.城市化过程中人口变动趋势对我国房地产开发的影响［J］.人口学刊，2004，（3）：45-48.

［6］Ramesh Kumar Jain.Houses Turn Gold as Prices Skyrocket［J］.Money Today，2011，（10）.

［7］骆永民.城市化对住房价格的影响：线性还是非线性？——基于四种面板数据回归模型的实证分析［J］.财经研究，2011，（4）：135-144.

［8］邓翔，孔红枚.基于动态面板模型的城市化与住房价格关系研究［J］.统计与决策，2013，（2）：105-107.

［9］李雄军，姚树洁.计划生育、城市化与我国住房市场的发展［J］.当代经济科学，2011，（5）：74-77.

［10］哈继铭.人口结构与城市化推动房地产发展［J］.中国房地信息，2007，（7）：28-29.

［11］杨静.中国人口变化趋势及其对经济趋势的影响［J］.中国经济参考，2012，（56）：65-75.

［12］Yasuhiro Sato，Kazuhiro Yamamoto.Population concentration，urbanization and demographic transition［J］.Journal of Urban Economics，2005，（58）：45-61.

［13］张立.论我国人口结构转变与城市化第二次转型［J］.城市规划，2009，（10）：35-44.

［14］叶青，叶越，徐琼.人口结构特征及对城镇化和房价的影响——基于湖北省第六次人口普查及有关资料［J］.调研世界，2012，（6）：40-44.

［15］James M.Poterba.Inflation Income Taxes and Owneroccupied Housing［J］.Harvard University，1980：1-30.