基于操纵稳定性的EPS转向系统鲁棒控制策略研究

翁敬良，严运兵

(武汉科技大学汽车与交通工程学院,湖北 武汉，430081)

新能源汽车具有电子化、轻量化、绿色环保等特性，已成为世界汽车发展的必然趋势。电动助力转向系统(Electric Power Steering System，EPS)作为新能源汽车研究方向之一，是继液压助力转向系统后出现的一种新型动力转向系统，具有轻型小巧、装配迅速、易于调整、噪声及废气污染小等优点。EPS系统在机械转向的基础上增加助力电机，通过电机提供转向时所需的辅助力矩，从而实现了汽车低速行驶时转向轻便和高速行驶时路感优良的要求[1]。但是，随着对汽车性能要求的不断提高，汽车高速行驶时的操纵稳定性也备受重视。因此，EPS系统的鲁棒性研究得到了广泛关注。Toshio Kohno等[2]将H∞控制理论应用到EPS控制系统；Parmar等[3]利用线性二次型调节器(LQR)和Kalman滤波技术设计了EPS系统控制器；吴文江等[4]运用鲁棒控制理论当中的LMI(Linear Matrix Inequalities)处理方法计算EPS系统控制器；刘照等[5]运用混合灵敏度设计方法设计了EPS系统鲁棒控制器；杨孝剑等[6]将电动助力转向系统当中电机电流的控制采用模糊神经网络PID控制方法进行控制；赵万忠等[7]提出 EPS 系统混合H2/H∞控制器，该控制器综合了H2控制和H∞控制的优点。以上控制方法在EPS的控制研究中取得了较大进展,但大部分是针对EPS系统本身的控制及其稳定性的研究，目前还未见关于将EPS系统加载到整车系统中作为一个整体控制对象来研究的报道。为此，本文针对装载EPS系统的车辆对转向轻便性、良好路感和整车操纵稳定性的综合要求，并考虑到该控制系统是一个多输入多输出(MIMO)的多变量模型[8]，提出将混合灵敏度方法[9-10]运用于EPS系统的控制策略，设计了H∞鲁棒控制器，以期提高整个系统的鲁棒性和稳定性，增强系统的抗干扰能力。

1 EPS系统动力学模型

EPS系统主要由扭矩传感器、车速传感器、电子控制单元 (ECU)、电动机和减速机构等部分组成，如图1所示。

为了分析问题方便，将电动助力转向系统模型进行适当的简化，得到EPS系统的动力学模型如下：

(1)

其中，

Ts=Ks(θh-θp)

(2)

Tm=KaId

(3)

式中:Jh为方向盘转动惯量；Jr为等效到转向柱的转动惯量；Jm为助力电动机的转动惯量；Bh为方向盘阻尼系数;Br为转向机构和前轮的当量阻尼系数;Bm为助力电机的阻尼系数;Th为方向盘输入力矩；Ts为扭矩传感器测得的扭矩值；Ta为电动机经减速机构作用到转向轴的助力力矩；Tr为等效到转向柱上的转向阻力矩；Tm为电动机电磁转矩；θh、θp和θm分别为方向盘、转向轴和电动机轴的转角；G1为电动机到转向轴的传动比；Ks为扭矩传感器的扭转刚度;Ka为电动机转矩系数；Id为电机电流。

设转向轴到前轮的传动比为G2，则有[11]：

(4)

式中：δf为转向轮转角。

1—扭矩传感器；2—减速机构；3—齿轮齿条式转向器；4—离合器；5—电动机;6—车速传感器

2 二自由度汽车数学模型

为了便于分析整车操纵稳定性的基本特性，本文采用线性二自由度汽车模型，如图2所示。该模型忽略了转向系统、悬架等因素的影响，且假定汽车沿x轴的前进速度u保持不变，直接以转向轮的转角为输入，即假定汽车只有侧向和横摆两个运动状态，则其动力学方程为：

Fy1、Fy2—地面对前、后轮的侧向反作用力；αf、αr—前、后轮的侧偏角；v—车辆侧向速度；u—车辆纵向速度；V—车辆质心速度；a、b—质心到前、后轴的距离；β—车辆的质心侧偏角

(5)

式中：Kf、Kr分别为前后轮的侧偏刚度；lf为车辆质心到前轴的距离；lr为车辆质心到后轴的距离；ωr为横摆角速度；m为汽车质量；IZ为汽车绕z轴的转动惯量。

在转向系统模型中，地面阻力矩等效到转向柱上的转向阻力矩Tr可由下式[11]确定：

(6)

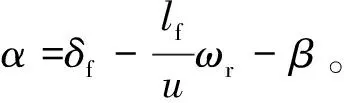
3 EPS系统广义被控对象状态方程

(7)

A=

4 EPS鲁棒控制器的设计

4.1 H∞混合灵敏度问题

图3所示为一个包含模型不确定性的反馈控制系统。图3中，G(s)为不包括模型不确定性因素的标称模型；u1为参考输入；u2为控制输入；e(t)为跟踪信号的误差；u(t)为控制输入;y为系统的输出；z为系统评价输出；WS为灵敏度加权因子；WR为输入灵敏度加权因子；WT为补灵敏度加权因子；F(s)为系统控制器。

图3 H∞混合灵敏度控制系统结构图

H∞混合灵敏度控制设计中包含灵敏度函数S、输入灵敏度函数R和补灵敏度函数T，其Laplace变换式分别定义为：

S(s)=(I+G(s)K(s))-1

(8)

R(s)=(I+G(s)K(s))-1K(s)

(9)

T(s)=(I+G(s)K(s))-1K(s)G(s)

(10)

式中：I为单位矩阵；K(s)为反馈控制器。

4.2 加权函数的选择

(11)

(2)补灵敏度函数。补灵敏度函数是参考输入r到系统输出y的传递函数矩阵，其奇异值越小，代表结构型不确定因素对系统的影响越小。通过引入补灵敏度函数加权因子WT减小‖H∞‖须满足如下关系：

(12)

(3)输入灵敏度函数。输入灵敏度函数加权因子是为了避开执行机构饱和而选取的，通常为常数。

由前所述，灵敏度函数和补灵敏度函数在系统相同频段时受S+T=I的限制。考虑到输入信号和干扰普遍具有低频特性以及结构型不确定性对高频的敏感，可以在低频时以减小‖S(s)‖∞为主，高频时以减小‖T(s)‖∞为主。通过将两个矛盾的指标所在的频率区域分开的方法避开S+T=I的限制条件，即：

(13)

式中：ε1和ε2为正数；Ω1和Ω2是没有交集的两个领域，其中Ω1为低频段，Ω2为高频段。

至此，系统的稳定性和跟踪性问题就转化成如图3所示的H∞混合灵敏度问题。

4.3 H∞鲁棒控制器设计

EPS控制系统设计不仅要考虑汽车的转向轻便性和良好的路感，还要考虑整车的操纵稳定性和抗干扰能力。基于此，对EPS的状态空间模型进行扩充，根据以上设计目标引入评价向量，得到广义被控对象并转换成标准的H∞控制问题。选取4个评价输出指标[5]如下：

混合灵敏度控制器的优劣很大程度上取决于灵敏度函数和补灵敏度函数的加权函数的选取，结合EPS系统特征以及系统对性能的要求，经反复多次仿真得到加权传递函数如下：

(14)

(15)

WR(s)=0.001

(16)

根据以上对被控对象名义模型和系统评价指标的分析与描述，利用鲁棒控制工具箱提供的sdiag和smult函数构造加权对角矩阵和广义被控对象，然后利用Matlab软件LMI工具箱中的hinflmi函数，求解得到输出反馈控制器K(s)和闭环系统的最优H∞性能指标ξ=1.2051。通过求解可知，满足Lyapunov方程[13]的正定实对称矩阵(即EPS闭环控制系统状态空间模型的函数矩阵A)的特征根值的实部均为负值，这验证了EPS闭环控制系统的稳定性。

5 仿真与结果分析

5.1 仿真方法

仿真计算在MATLAB/Simulink环境下进行。假定车速恒定为25km/h，方向盘上施加5N·m的阶跃输入转矩，仿真时间为10s。计算中用到的汽车参数与EPS系统参数如表1所示。

表1 汽车与EPS系统的结构参数

5.2 助力特性分析

图4所示为加载了基于H∞混合灵敏度控制策略的EPS系统的汽车在不同方向盘转矩输入下电动机所提供的助力力矩。由图4中可见，随着输入力矩的增大，助力力矩随之增大，表明基于H∞混合灵敏度算法设计的EPS系统控制器具有良好的助力性能。

5.3 路感仿真结果分析

图5所示为扭矩传感器测量值。由图5中可见，基于H∞混合灵敏度控制的EPS系统扭矩传感器测量值很快进入稳态，表明其对方向盘输入阶跃响应具有良好的跟随性，可使驾驶员获得良好的路感。

5.4 操纵稳定性分析

图6所示为加载了基于H∞混合灵敏度控制策略的EPS系统与没有加载EPS的汽车转向系统横摆角速度阶跃响应曲线。从图6可以看出，加载了EPS系统之后，汽车横摆角速度响应曲线的稳定时间明显减短，超调量从97%降至18%，表明汽车加载EPS系统后，反应时间加快，并且很快达到稳定，同时抑制了振荡，汽车的操纵性能得到显著改善。

图4 不同方向盘转矩输入下电动机输出的助力力矩

Fig.4Assistanttorqueoutputfromthemotoratdifferenttorgueinputofsteeringwheel

图5 扭矩传感器测量值对比图

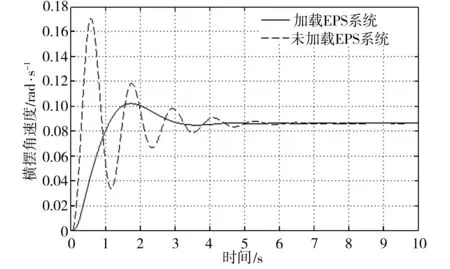
图6 横摆角速度阶跃响应曲线

为了验证基于H∞混合灵敏度控制策略的EPS系统具有较强的稳定鲁棒性，在仿真模型中加入白噪声信号功率谱密度为0.01的扭矩传感器测量噪声和路面干扰，并将此控制策略的控制效果与PID控制系统控制效果进行对比。两种控制策略下的横摆角速度阶跃响应曲线如图7所示。由图7中可见，加载了EPS系统的汽车其横摆角速度阶跃响应保持了较好的跟随性，能在较短的时间内达到稳定状态，表现出极好的抗干扰性能，表明H∞混合灵敏度控制器对于路面干扰和扭矩传感器测量噪声有明显的抑制作用。

图7 加入噪声后横摆角速度阶跃响应曲线

Fig.7Stepresponsecurveoftheyawratesbyaddingnoise

图8所示为汽车质心侧偏角β阶跃响应曲线。由图8中可见，加入噪声后质心侧偏角的响应有一定的震荡，但波动很小，表明了加载基于H∞混合灵敏度控制策略的EPS系统后汽车具有较稳定的转向姿态。

综上分析，基于H∞混合灵敏度控制的EPS系统有助于提高车辆转向时的轻便性以及操纵稳定性。

图8 加入噪声后质心侧偏角阶跃响应曲线

Fig.8Stepresponsecurveofcentroidside-slipanglebyaddingnoise

[1] Kim J H,Song J B．Control logic for an electric power steering system using assist motor[J].Mechatronics, 2002,12(3):447-459.

[2] Toshio Kohno, Shinji Takeuchi,Minekazu Momiyama, et al.Development of electric power steering (EPS) system with H∞control[J]. SAE Technical Paper，2000(1)：113-118.

[3] Parmar M,Hung J Y.A sensorless optimal control system for an automotive electric power assist steering system[J]. IEEE Transactions on Industrial Electronics,2004,51(2):290-298.

[4] 吴文江,郝金魁.基于MC9S12DP256的电动助力转向系统硬件设计[J].中国工程机械学报,2006，4(4):494-497.

[5] 刘照，杨家军，廖道训.基于混合灵敏度方法的电动助力转向系统控制[J].中国机械工程，2003，14(10):874-876.

[6] 杨孝剑.汽车电动助力转向系统的动力学分析与控制研究[D].合肥：合肥工业大学，2003.

[7] 赵万忠，施国标，林逸，等.基于混合H2/H∞控制的电动助力系统转向路感[J]. 机械工程学报，2009，45(4):142-147.

[8] 胡爱军，施国标，林逸.电动助力转向系统LQG/LTR控制[J].农业机械学报,2009，40(5):12-15，28．

[9] 樊树军.H∞混合灵敏度设计问题仿真研究[D].哈尔滨：哈尔滨工业大学，2010．

[10]田大庆.基于鲁棒控制理论的汽车电动转向助力系统控制技术研究[D].成都：四川大学，2006．

[11]唐新蓬,杨树.电动助力转向系对汽车角输入响应影响的仿真[J].汽车工程,2004,26(3):314-318．

[12]余志生.汽车理论[M].北京：机械工业出版社，2000.

[13]吴敏,桂卫华,何勇.现代鲁棒控制[M].长沙：中南大学出版社，2006:21-27.