混合测序技术在高通量测序中的应用
2014-03-28李成
李成
混合测序技术在高通量测序中的应用
李成
介绍了高通量测序在面向大样本时所面临的问题,分析了高通量测序技术的原理和特点及其在解决大样本测序时的技术优势,并总结了检测矩阵的构建方法,指出了混合测序能够应用于部分高通量测序实验并可大幅节约测序成本,展望了混合测序技术在高通量测序中的应用前景。
样本混合;高通量测序;群试;分离矩阵
0 引言
随着高通量测序技术的不断发展和测序成本的不断降低,利用高通量测序技术进行医学诊断具有较好的前景。同时,众多医学研究表明,许多疾病与某些稀有变异基因密切相关,针对某些已知稀有变异基因的检测能够预判或诊断出与之密切相关的疾病。在新一代测序技术应用于这些稀有变异基因检测的过程中,有2个方面是应用中亟待解决的问题:
(1)新一代测序技术带给人们大量遗传信息的同时,却成为限制其广泛应用的一个障碍。新一代测序仪的一个测序流程能够产生巨量的片段信息,如ABI公司的新一代测序平台SOLID单次运行,便可分析6 GB的碱基序列;Illumina Genome Analyzer测序系统仅在2 h的运行时间里就可得到10 TB的信息[1],这些巨量信息仅仅用来提高某些固定碱基位点的测序覆盖度,无疑是极为浪费的。(2)在针对此类稀有变异疾病进行大量人群筛查时,一个测序通道只针对一个个体样本,而如今二代测序仪最多只有8个通道,因此一次测序流程只能测8个个体样本,在针对大量人群稀有变异筛查的医学检验中。简单地利用测序仪逐个样本筛查,成本是不可想像的。
将样本混合后进行检测能够均衡两方面,并可充分利用新一代测序仪的测序性能,从而大大降低测序成本。但仅仅简单的混合无法分辨检测到的变异片段来自于哪个样本,如何将所得到的测序结果溯源,即找到测序结果片段的源样本,是这种方法应用的前提。
目前已有2类方法可进行混合:第一类方法是每个样本序列被打断后,成为适合测序的小片段,首先为这些小片段加上条形码,即为属于每个样本的序列片段加上了一个“身份标志”,然后再进行混合测序。测序找到含稀有变异的片段时,通过条形码这个身份标志,能够分辨出属于哪一个样本[2]。但这种方法的实现需要在测序准备时、样本打断后进行,而且为每个样本的一批片段标志条形码,增加了一个工作步骤,并且需要逐样本添加,保证每个样本的条形码唯一,所以大大增加了工作量。第二类方法就是本文要重点讨论的混合测序(Overlapping pooling)技术。其原理是将样本按照一定规律进行编码混合,之后进行测序,根据混合测序的检测结果和编码规律再进行反向解码,从而找到含变异的样本。
1 Overlapping pooling技术简介
以一个检测实例说明样本混合方法的原理。设待测样本有20个,图1表示了一种简单的网格分组方法,但这种方法的成功应用基于一个前提,即所有样本仅有一个阳性样本(如图1(a)所示),若含2个以上的阳性样本,则无法成功解码(如图1(b)所示)。
将20个样本分别编号为1~20,分为A、B、C、D、E、Ⅰ、Ⅱ、Ⅲ、Ⅳ共9组,分组结果如图2所示。
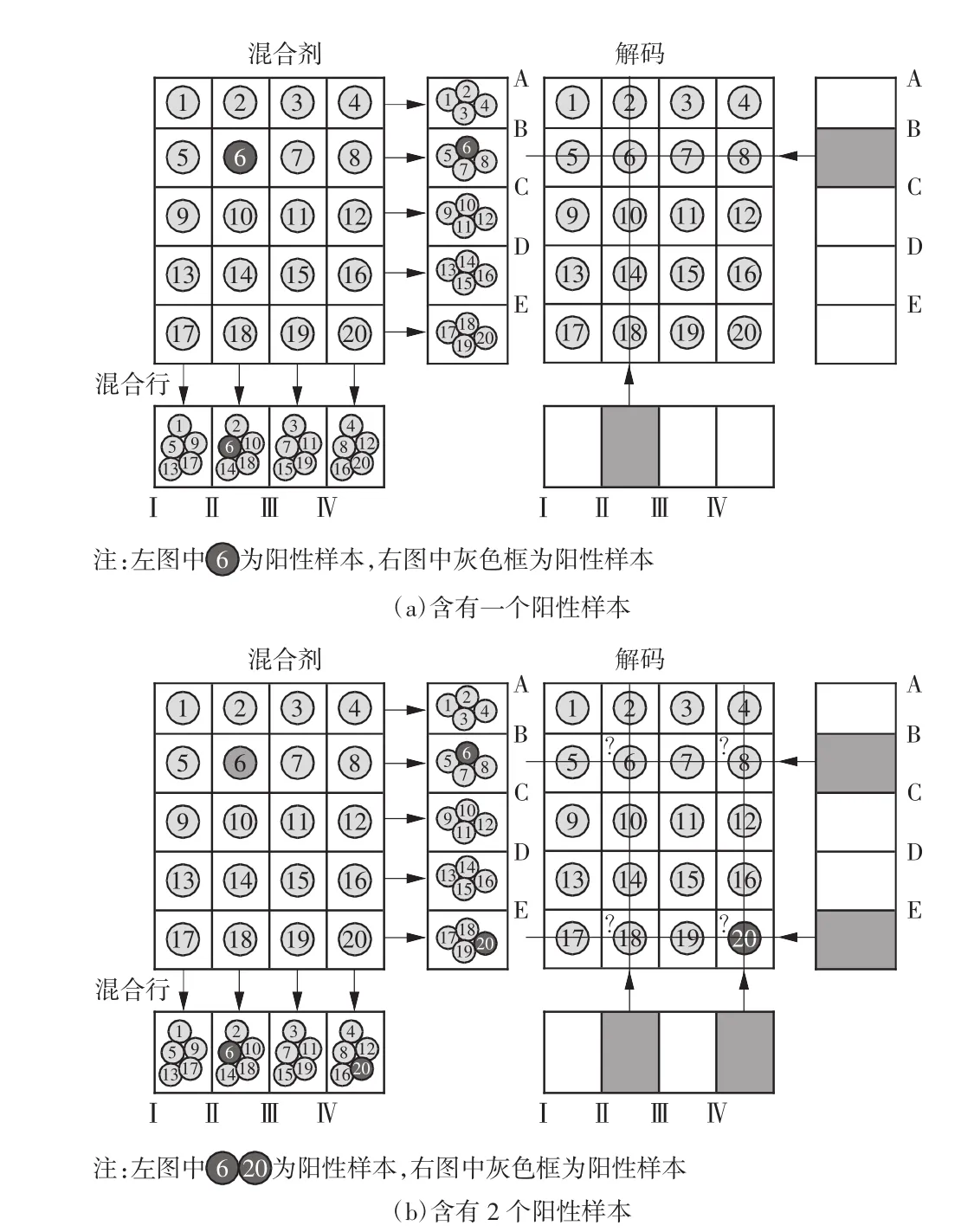
图1 样本混合方案设计检测阳性样本

图2 样本混合方案分组示意图
根据图2对9个组中的混合样本分别进行检测,一共检测9次,就可以判断出阳性样本是哪一个。如图1(a)所示,假设9次检测结果中,B组和Ⅱ组检测结果为阳性,说明这2组含有阳性样本,再由前提条件只有1个阳性样本,则根据图2的分组规则,只有6号样本为2组共同所有,所以6号样本为阳性。这样通过样本混合分组,仅用9次检测就找到了20个样本的某个阳性样本,从而避免了20个样本的逐个检测。
这种检测算法可以用一个元素为0或1的检测矩阵M来具体表示。设欲检测样本总数量为N,群试设计方案中共要进行T次检测,则有一个T×N的(0,1)矩阵M,各列代表各个样本,各行代表各组的检测池(即一次检测),Mij表示第i行和第j列相交的矩阵元素,Mij=1表明在所设计的实验中要将第j号样本混入到第i个检测池中,即参与第i个检测池的检测实验;Mij=0则表明第j号样本不用加入到第i个检测池中。例如,上节中样本混合的分组方式可用检测矩阵表示,如图3所示。

图3 样本混合方案对应检测矩阵
检测矩阵的每一列对应一个样本,每一行代表一个检测池(即一次检测),若某一列对应的样本为阳性样本,则我们称此列为阳性列;同样,矩阵中代表检测结果为阳性的检测池的行称为阳性行。观察上例矩阵,任意一个列向量都与其他列不同,而这正是单阳性样本能够正确解码的条件。但这种简单的分组方式不能够解决多个阳性样本的检测问题,如图1(b)所示,如果6号和20号样本均为阳性,则会使B、E、Ⅱ、Ⅳ4组检测为阳性,而4组阳性的原因存在 {8,18}、{6,20}、{6,8,18}、{6,8,20}、{6,18,20}、{8,18,20}、{6,8,18,20}多种阳性样本组合的可能性,故这种分组方式不能满足检测多个阳性样本的要求。
研究人员经过对群试理论的深入研究,发展了能够检测多个阳性样本的Overlapping pooling方法。因为阳性样本能够通过检测矩阵正确判断的条件是结果列向量U(D)与其他任意d列的布尔和均不同,有了这种唯一性才能够判断出是哪d列对应样本阳性使结果列向量出现此结果。所以在检测矩阵M设计过程中,要想检测出d个阳性样本,必须保证对于M中任意的2个不同的d列D1,D2,总有U(D1)≠U(D2),满足这种性质的(0,1)矩阵称之为d-可分(dseparable)矩阵。但可分矩阵的解码复杂度过高,因而Kautz和Singleton[3]提出了d-分离矩阵的定义:对于一个(0,1)矩阵M,若其中任意一列均不能够被其他任意d列的布尔和所覆盖(在(0,1)矩阵中,若一列A中所有的1元素在另一列B同样位置上都有1元素,则称A被B覆盖),M称为d-分离(ddisjunct)矩阵。d-分离矩阵可用来检测最多d个阳性样本。其解码过程较简单,只需将矩阵中每一列C与检测结果向量进行比较,若C被结果向量覆盖,则C所代表的样本为阳性,反之为阴性。在大样本中稀少突变的检测过程中,各种实验误差导致的检测错误往往是不可避免的,因而所设计的检测矩阵还应当具备一定的容错性。D′Yachkov等[4]提出了容错矩阵的概念,给出了(d;z)-可分矩阵的定义和其纠错能力。但正如d-可分矩阵、(d;z)-可分矩阵解码方式的时间复杂度过高,于是Macula提出de-分离矩阵的概念[5]:一个d-分离矩阵M称为de-分离,若对于M中任意的d+1列中存在一列,有e+1行均为1,而其他d列的这些行均为0。1996年,Macula定义de-分离矩阵时认为其能够纠正e个错误,但2003年Hwang[6]提出de-分离矩阵无法纠正e个错误,随后D′Yachkov等[7]给出了证明,并重新定义了dz-分离矩阵M:对于M中任意的d+1列中存在一列,有z行均为1且不能被其他d列覆盖。Yachkov认为dz-分离矩阵至少能够查出z-1个错误和纠正(z-1)/2个错误。
2 Overlapping pooling检测矩阵构建方法
在利用Overlapping pooling技术进行大样本检测实验时,要通过构建检测矩阵实现混合方案和解码的确定。因此,如何进行d-分离矩阵和dz-分离矩阵的构建是此技术应用的关键,其中,关于分离矩阵构建主要有以下3种方法,现分别介绍如下。
2.1 区组设计
Kautz和Singleton[3]在20世纪60年代基于区组设计的研究给出了一种d-分离矩阵的构造方法,但这种方法的发展受到信息论中参数最优化理论的限制,一直难以找到最优的区组。
2.2 横向设计
最简单的横向设计就是上文提到的网格设计。针对网格设计只能检测单阳性样本的缺陷,Nicolas等[8]提出了横向转移设计(shifted transversal design,STD)方法,将所测样本分为若干组分别混合检测,并且每一组的混合方案均不同,每个样本在每一组的被混合次数一致,并且能够成功解码。这种方法具有灵活的设计能力,能根据检测样本数、含有的阳性样本个数、可能的错误发生率进行高效的混合方案设计,是目前所知的最优的设计方法。这种方法应用在药物检测领域取得了不错的效果[9]。
2.3 直接构造
Macula[10]给出了一个利用有限集的子集之间的包含关系设计检测矩阵的方法:设M(n,k,d)是的(0,1)矩阵(d≤k 随着近年来高通量测序技术的飞速发展,查找大量样本中含稀有变异的样本已成为一种重要应用。为充分利用测序仪的单通道测序能力,有必要将样本混合后进行测序,若利用Overlapping pooling技术将样本有序混合,则可不必添加标志用的条形码。实际应用中,简单的网格设计混合或二进制混合不能发现2个以上含变异的阳性样本,如Snehit Prabhu等[11]介绍的基于Illumina′s Genome Analyzer-2测序平台的混合方法中,一个混合检测池不能含有2个以上的阳性样本。为检测出混合池中含2个以上的阳性样本,Erlich等[12]设计了一种DNA Sudoku混合方法,混合之后添加条形码,再进行测序。该设计能够针对阳性样本数和可能的检测错误灵活设计混合方案,但各组间的混合池数目要求互质。Xin等[13]基于横向设计方法进行了酵母双杂交相互作用组定位的实验验证,与逐个样本的检测相比,该方法大大节约了成本,提高了检测效率,同时仍表现出相当的灵敏性。 Overlapping pooling技术源于群试理论,在高通量测序平台上,这种实验设计方法体现了相当的应用价值。受限于群试理论的发展,这种混合方法在定量检测上仍缺乏应用,如一些常见的血液检测中,每个血液样本均和试剂反应后测得一定的值,通过测量值是否在标准范围内来判断是否为阳性样本。这种情况下不能基于“含有”或“不含有”进行判断,要结合测量值才能判断。若能够实现定量检测的混合实验设计和解码方法,则在众多医学常规检测中均可应用。如Amin Emad等[14]提出了半定量的群试方法,为这种方向的应用提供了一定的参考价值。 [1] Shendure J,Ji H.Next-generation DNA sequencing[J].Nature Biotechnology,2008,26(10):1 135-1 145. [2] Patterson N,Gabriel S.Combinatorics and next-generation sequenc- (▶▶▶▶)(◀◀◀◀)ing[J].Nature Biotechnology,2009,27(9):827. [3] Kautz W H,Singleton R C.Nonrandom binary superimposed codes[J]. IEEE Trans Inform Thy,1964,10:363-377. [4] D′Yachkov A G,Rykov V V,Rachad A M.Superimposed distance codes[J].Problems Control Inform Thy,1983:12:1-13. [5] Macula A J.Error-correcting nonadaptive group testing with dPeP-disjunct matrices[J].Discrete Applied Mathematics,1997,80:217-222. [6] Hwang F K.On Macula′s error-correcting pool designs[J].Discrete Mathematics,2003,268:311-314. [7] D′Yachkov A,Frank H.A construction of pooling designs with some happy surprises[J].Journal of Computational Biology,2005,12:1129-1 136. [8] Thierry N.A new pooling strategy for high-throughput screening:the shifted transversal design[J].BMC Bioinformatics,2006,7:28. [9] Raghunandan M K,Peter J W.PoolHITS:a shifted transversal design based pooling strategy for high-throughput drug screening[J].BMC Bioinformatics,2008,9:256. [10]Macula,Anthony J.A simple construction of d-disjunct matrices with certain constant weights[J].Discrete Mathematics,1996,162:311-312. [11]Prabhu S,Pe′er I.Overlapping pools for high-throughput targeted resequencing[J].Genome Research,2009,19:1 254-1 261. [12]Erlich Y,Chang Y.DNA sudoku—harnessing high-throughput sequencing for multiplexed specimen analysis[J].Genome Research,2009,19:1 243-1 253. [13]Xin X F,Rual J F.Shifted transversal design smart-pooling for high coverage interactome mapping[J].Genome Research,2009,19:1262-1 269. [14]Emad A,Milenkovic O.IEEE International Symposium on Information Theory,Cambridge,JUL 01-06,2012[C].Urbana USA:IEEE,2012. (收稿:2013-05-07 修回:2013-11-25) (栏目责任编校:陈建新) Application of pooled sequencing technology to high-throughout sequencing LI Cheng The problems of high-throughout sequencing technology are introduced when used for large samples,whose principle,characteristics and advantages are also analyzed.The construction of the test matrix is summarized.It's pointed out that the introduction of pooled sequencing into some high-throughout sequencing experiments may result in decreased cost.The prospect of pooled sequencing technology is explored in the high-throughout sequencing.[Chinese Medical Equipment Journal,2014,35(9):116-118,121] composite sample;high-throughout sequencing;group testing;disjunct matrix R318;O151.21 A 1003-8868(2014)09-0116-04 10.7687/J.ISSN1003-8868.2014.09.116 李 成(1979—),男,工程师,主要从事生物医学工程、生物医学信息学方面的研究工作,E-mail:licheng18@163.com。 210002南京,南京军区联勤部药品仪器检验所(李 成)3 Overlapping pooling技术在高通量测序中的应用
4 Overlapping pooling技术的发展和面临的问题
(Institute of Drug and Instrument Control,Joint Logistics Department of Nanjing Military Area Command,Nanjing 210002,China)
