PID/ADRC控制器在四旋翼无人飞行控制中的应用

刘 刚,王 彪, 曹云峰

(1.南京航空航天大学 自动化学院，南京 210016；2.南京航空航天大学 高新技术研究院，南京 210016)

四旋翼无人飞行器是一种能够垂直起降的多旋翼直升机，具有体积小、结构简单、易于维护、机动性能好等优点，近年来成为国内外研究的热点[1].它是一种具有六自由度和4个输入的欠驱动飞行器，采用了轴对称布局，其机械结构简单，4个旋翼均匀分布.其欠驱动、强非线性、强耦合等特性给控制器设计带来了不少问题.另外由于其动力学模型的复杂性、模型参数不确定性和建模不精确性等问题，造成其对控制器的鲁棒性、抗干扰性提出了高要求.

针对以上问题，国内外许多研究机构进行了相关的研究.文献[2-3]采用了经典PID控制方法进行控制系统设计，但PID控制效果依赖于模型的精度；文献[4]首先将复杂的四旋翼动力学模型分解为内外环子系统，并在此基础上采用了反步法以及滑模控制进行控制系统设计,但其控制输出有抖动，影响了控制效果；文献[5]采用LQ控制方法设计控制律，但其忽略了模型中的非线性因素，影响了控制效果；文献[6]应用动态逆(DI)方法处理对象的非线性，将系统等效为一个解耦但存在不确定性的线性对象，并且应用定量反馈理论(QFT)设计了控制器克服了对象参数的不确定性，但此方法对模型的精确性有一定的要求.

经典PID控制以其简单易懂的控制结构，良好的实用性和参数调节方便等优点倍受青睐.自抗扰控制(active disturbances rejection control，ADRC)是近年来逐渐发展起来的一种控制方法[7-8]，自抗扰控制一方面继承了经典PID控制的优点，且不依赖于模型，只利用误差反馈进行控制，以及采用非线性反馈提高控制性能；另一方面，采用扩张状态观测器(extended state observer, ESO)对扰动(外部扰动和内部扰动)进行实时估计和补偿.因此ADRC比较适合用于四旋翼无人飞行器难以建立精确模型，强耦合，强非线性等的复杂控制问题.

本文以作者所在实验室的四旋翼无人飞行器X450为研究对象，建立了机体运动模型和电机模型.由于飞行器控制中对姿态控制的要求较高且控制难度相对较大，位置和线速度控制相对简单，因此采用内、外环回路控制思想设计控制器，其中内环回路采用自抗扰控制方法设计姿态控制器，外环回路采用经典PID控制方法设计位置与线速度控制器.仿真及实验结果表明，四旋翼飞行器在悬停点附近工作时该控制方法是可行及有效的.

1 飞行器建模及自抗扰基本原理

1.1 四旋翼飞行器模型

本文所研究的是X型分布四旋翼结构，主要根据物理机理进行建模[9-10]，假设四旋翼飞行器是刚体，地面为惯性参考系.惯性坐标系和机体坐标系都满足右手直角坐标系规则，如图1所示.惯性坐标系以北—东—天分别作为xn，yn，zn轴方向，机体坐标系zb由右手直角坐标系规则垂直于xb-ob-yb.

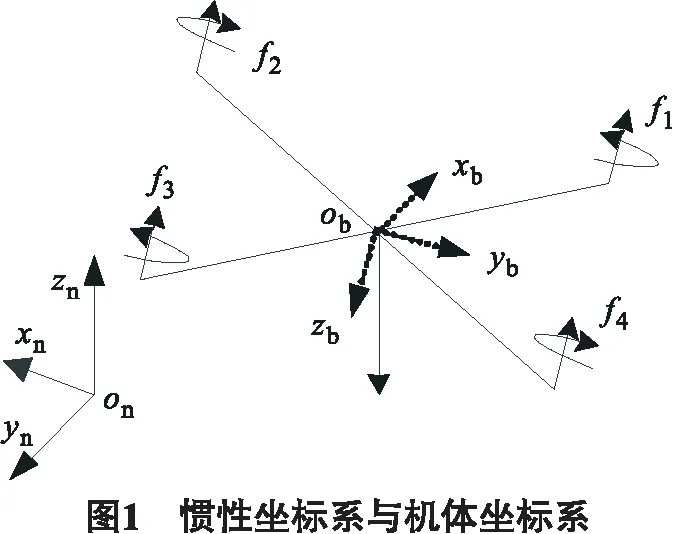
在机体坐标系中建立的飞行器运动方程如下：

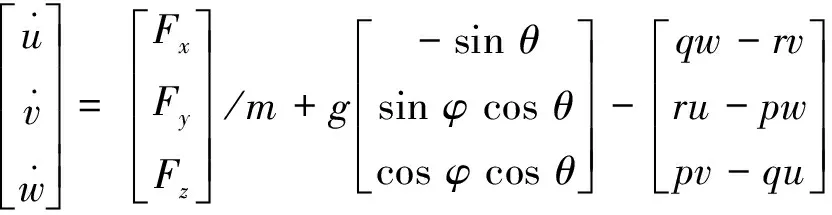
(1)

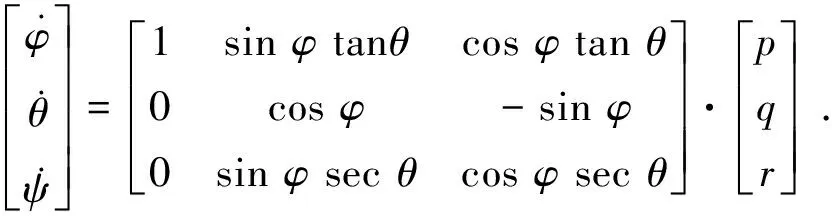
(2)

(3)

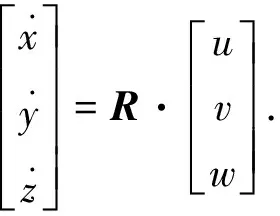
(4)

其中，u，v，w为机体坐标系下三轴向的线速度；φ、θ、ψ为机体坐标系下三轴向的滚转角、俯仰角、偏航角；p，q，r为机体坐标系下三轴向的姿态角速率；x，y，z为惯性坐标系下飞行器的位置坐标；m为飞行器质量；g为当地重力加速度；Fx，Fy，Fz为空气动力在机体坐标系下的分量；Qx，Qy，Qz为外合力矩在机体坐标系下的分量；Ix，Iy，Iz为轴向转动惯量；R为机体坐标系到惯性坐标系的转换矩阵.

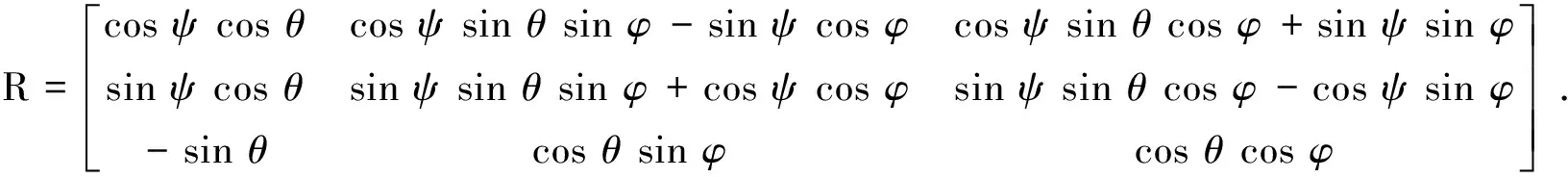
机体坐标系下四旋翼飞行器受到的空气动力和力矩如下：

(5)

(6)

其中，kT、Ω分别为旋翼升力系数和转动角速度，kM为反扭矩系数.

四旋翼的动力系统是由4个电机组成的，小型直流电机近似为如下惯性环节：

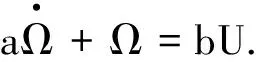
(7)

其中，a,b为系数，U为输入PWM信号.

众所周知，飞行器模型具有建模不精确、参数变化大、耦合性强等特点，因此可以采用自抗扰控制方法解决此类问题.

1.2 自抗扰控制器的基本原理

自抗扰控制(ADRC)由韩京清提出[11]，该控制策略对经典PID控制进行了4个方面的改进：

1) 安排过渡过程；

2) 采用跟踪微分器对被控对象提取微分信号；

3) 由非线性扩张观测器实现扰动估计和补偿；

4) 由误差的P、I、D非线性组合构成非线性PID控制器.

设带有未知扰动的不确定对象为：

(8)

其中f()为不确定函数，w(t)为未知外扰，u、y分别为系统输入和输出，b0为已知常数.其ADRC结构如图2所示.

取对象的状态变量为：

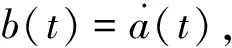
(9)

构造式(8)的非线性扩张状态观测器(ESO)方程如下：

(10)

其中β1,β2,…,βn+1为可调参数;f1(·),f2(·),…,fn+1(·)为适当选取的非线性连续函数.通过对各参数的选择，可令系统(10)的各状态变量跟踪系统(9)的扩张状态变量，即有：

z1(t)→x1(t),…,zn(t)→xn(t),zn+1(t)→xn+1(t).

(11)

ADRC通过跟踪微分器(TD),为参考输入安排过渡过程，得到参考输入v(t)及其各阶导数的近似跟踪值.最终可得到系统的控制量为：

u(t)=k1h1(v1-z1)+k2h2(v2-z2)+…+knh(vn-zn)+zn+1/b0.

(12)

其中，h1,h2,…hn+1为适当的非线性函数;k1,k2,…kn为常系数;zn+1/b0起到了补偿系统扰动的作用，增强了控制系统的鲁棒性.

2 四旋翼飞行器控制系统设计

根据四旋翼动力方程(1)～(4)式可以将控制系统设计为内外环结构[12]，如图3所示.内环采用自抗扰控制，外环采用经典PID控制.

2.1 内环自抗扰控制律设计

内环控制分为3个独立的回路，分别为滚转控制回路，俯仰控制回路和偏航控制回路.自抗扰控制器由跟踪微分器、状态扩张观测器和非线性状态误差反馈控制，其核心部分是状态观测器.

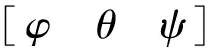
(13)

其中，b0=kM/Iz.

1)偏航运动ADRC的跟踪微分器(TD)方程：

(14)

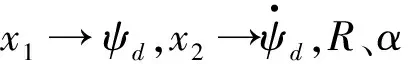
2)偏航运动ADRC的扩张状态观测器(ESO)方程：

(15)

式中，β1、β2、β3为状态误差反馈增益，影响ESO的收敛速度.

3)偏航运动ADRC的非线性状态误差反馈控制量的形成.

(16)

以上各式中饱和函数fal(e,α,δ)的作用为抑制信号抖振，表示为：

(17)

式中δ为fal函数的线性区间宽度.

2.2 外环PID控制律设计

在实现内环姿态控制的基础上，设计四旋翼无人直升机的外环控制.PID是经典的控制方法，具有控制律简单，以及实际控制效果好的优点，适合外环路的控制需要.

由图2可以看出外环控制律包含线速度控制和位置控制2部分.三方向位置控制如下：

(18)

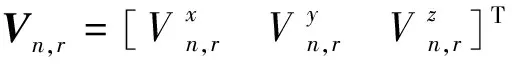
期望的机体系下线速度：

(19)

三方向线速度控制律如下：

(20)

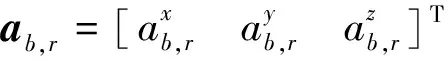
通过所得的机体系下三方向期望线加速度控制量,可以推导出期望的滚转角控制量φr、期望的俯仰角控制量θr和四旋翼垂向控制量总距δcol.根据式(6)可推导出下式：

(21)

整理后得：

(22)

其中，cosθcosφ项补偿了机体在俯仰和滚转运动时的升力损失.

3 控制系统仿真验证

本文使用Matlab/Simulink对系统进行仿真，采用作者实验室所设计的小型四旋翼无人机，相关参数如表1.

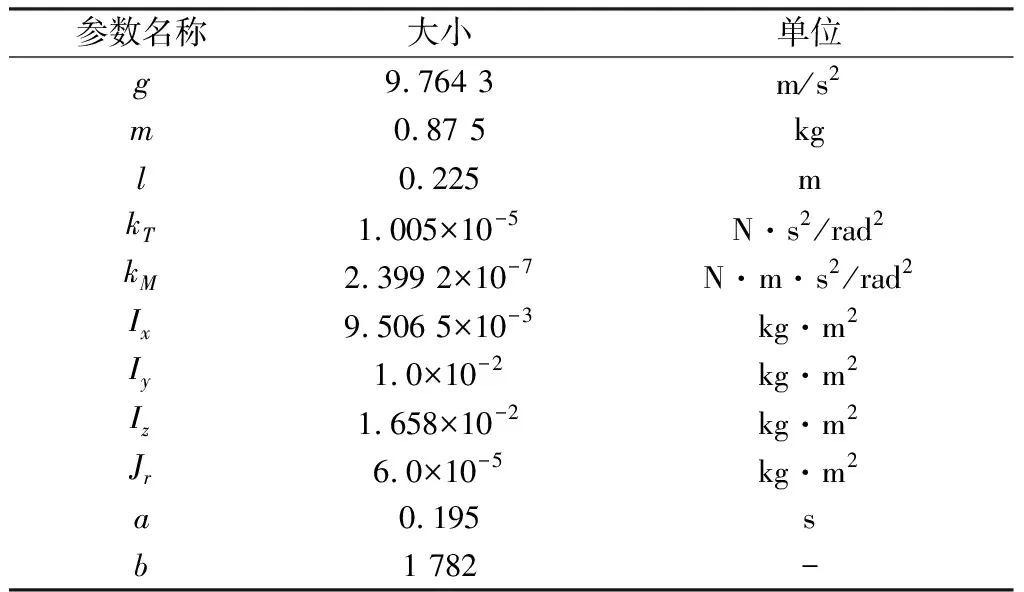
表1 小型四旋翼无人机的相关参数

下面通过仿真说明ADRC是如何安排过渡过程(TD)和对各状态量进行观测(ESO)的.在小角度下仿真，设飞行器初始各姿态角和角速率为0，给定各姿态角期望值为φd=0.1，θd=0.2，ψd=-0.2，并且对反馈状态加入随机噪声.

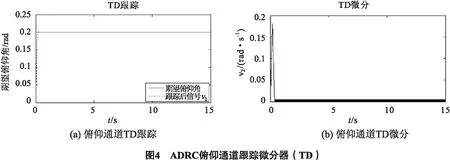
由图4所示，v1信号能快速跟踪θd信号，信号v2是输入θd的广义微分；可以看出TD平滑了θd的变化，增强了ADRC的鲁棒性.

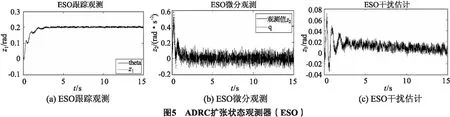
ESO是整个ADRC的核心部分，ESO的观测效果直接影响整个ADRC的使用情况.如图5(a)、(b)所示，ESO观测器能很好地观测角度θ和角速率q的值，图5(c)是ESO实时估计的系统扰动.通过ESO能将系统改造成串联积分型，并对系统扰动进行实时估计并补偿.

因此可以看出内环采用自抗扰控制可以对内扰和外扰进行估计补偿，可以较好地减轻模型不精确带来的问题.

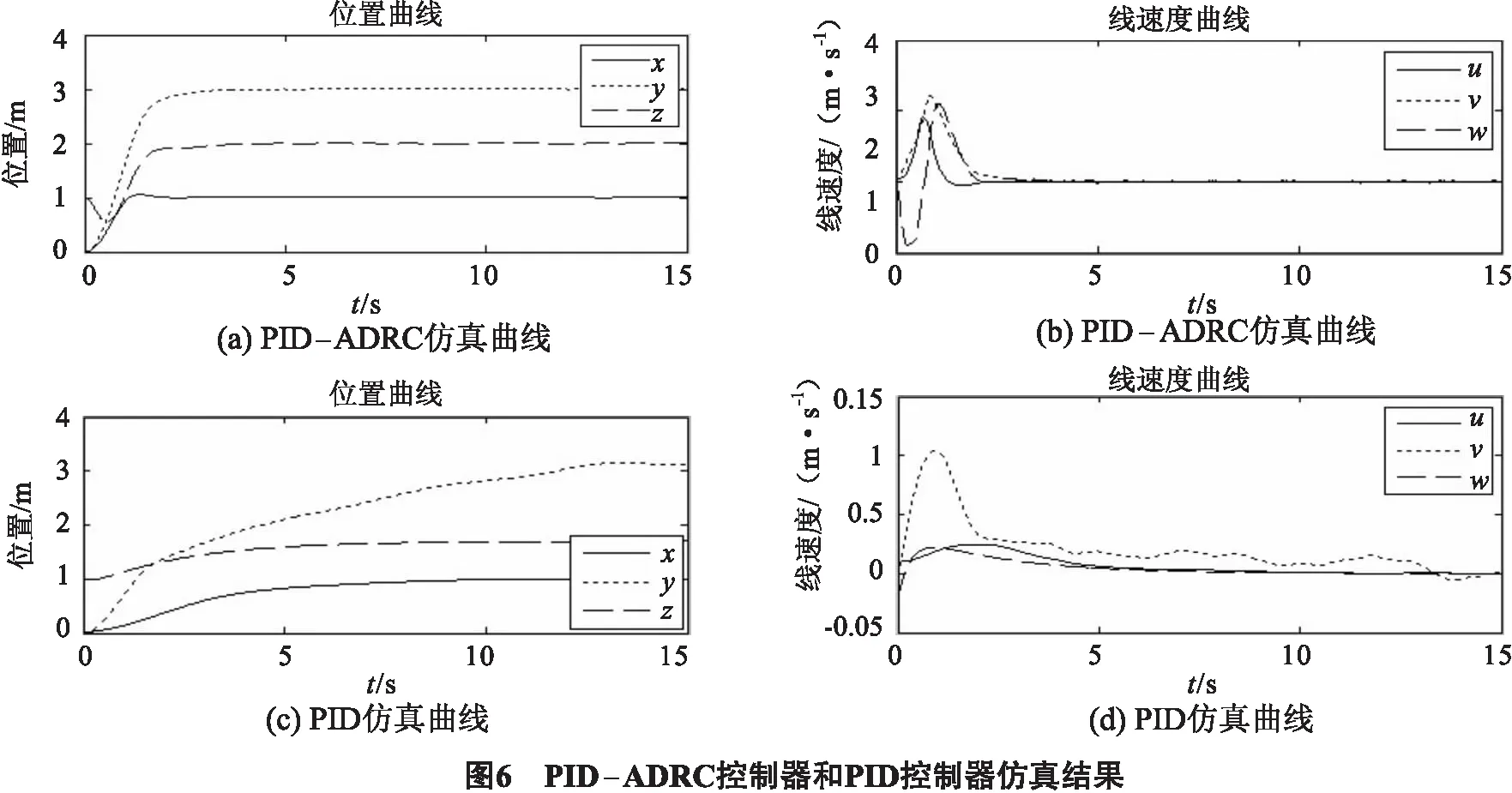
下面将PID-ADRC控制器和PID控制器仿真结果进行对比，设定飞行器初始值为x=y=v=0，z=1 m，u=0.1 m/s，w=-0.2 m/s，姿态φ=0.2 rad，θ=ψ=0，最终使飞行器悬停于位置(x，y，z)=(1，3，2).

由图6(a)、(b)可知，采用PID/ADRC控制结构的四旋翼飞行器能快速平稳地飞向预定位置并且悬停于稳定点，控制效果良好；图6(c)、(d)采用的是PID控制器，四旋翼飞行器也能悬停于预定位置，但过程较长，且震荡比前者大，控制效果显然没有采用PID/ADRC控制结构的控制效果好.仿真结果表明，内环采用自抗扰控制能适量地弥补模型的不确定性和强耦合性，内环自抗扰和外环PID控制的组合是有效的.

4 结语

本文建立了机体运动模型和电机模型，内环采用了自抗扰控制方法设计控制器，外环则采用经典PID控制方法设计控制器，仿真结果表明ADRC控制对内扰和外扰能进行较好的估计补偿，此控制方法具有较好的控制效果.后续工作中，可以将设计好的控制器运用到四旋翼无人飞行器平台上验证控制效果.

参考文献:

[1] 聂博文，马宏绪，王剑，等. 微小型四旋翼飞行器的研究现状与关键技术[J].电光与控制，2007，14(6)：113-117.

[2] 宿敬亚，樊朋辉，蔡开元. 四旋翼飞行器的非线性PID姿态控制[J].北京航空航天大学学报，2011，37(9):1054-1058.

[3] SALIH A L, MOGHAVVEMI M, MOHAMED H A F, et al. Modelling and PID controller design for a quadrotor unmanned air vehicle[C]//Automation Quality and Testing Robotics (AQTR), 2010 IEEE International Conference on. IEEE, 2010(1):1-5.

[4] HU Q, FEI Q, WU Q, et al. Research and application of nonlinear control techniques for quad rotor UAV[C]//Control Conference (CCC), 2012. IEEE, 2012: 706-710.

[5] BOUABDALLAH S, NOTH A, SIEGWART R. PID vs LQ control techniques applied to an indoor micro quadrotor[C]//Intelligent Robots and Systems, 2004. Proceedings 2004 IEEE/RSJ International Conference on. IEEE, 2004, 3: 2451-2456.

[6] 单海燕. DI/QFT 控制器在四旋翼无人直升机飞行控制中的应用[J]. 电光与控制, 2008, 15(12): 68-71.

[7] 韩京清. 自抗扰控制技术[M].北京：国防工业出版社，2008.

[8] 韩京清.从PID技术到自抗扰控制技术[J].控制工程，2002,9(3):13-18.

[9] 吴森堂，费玉华.飞行控制系统[M].北京：北京航空航天大学出版社，2005.

[10] 申珊颖. 斜十字四旋翼飞行器试验建模与控制技术研究[D]. 南京：南京航空航天大学，2013.

[11] 刘金琨. 先进PID控制Matlab仿真[M].北京：电子工业出版社，2011.

[12] 蔡国玮，陈本美，王彪，等. 无人驾驶旋翼飞行器系统[M]. 北京：清华大学出版社，2012.