M-矩阵与其逆矩阵的Hadamard积特征值的新下界
2014-03-27高美平
高美平
(文山学院 数学学院,云南 文山 663000)
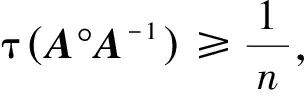
本文继续对M-矩阵A与其逆矩阵A-1的Hadamard积的最小特征值τ(A°A-1)的下界进行研究,得到关于τ(A°A-1)的不等式.
1 符号与引理
记N={1,2,…,n};Rn×n表示实n阶矩阵所成的集合;ρ(p)表示n×n阶非负矩阵P的Perron根;τ(A°A-1)表示非奇M-矩阵A与其逆矩阵A-1的Hadamard积最小特征值.

为了叙述方便,给出以下记号:
引理1[6]设A=(aij)∈Rn×n是行严格对角占优矩阵,A-1=(bij),则|bji|≤sji|bii|,j≠i.



引理5[7]设A=(aij)∈Rn×n,是行严格对角占优的M-矩阵,A-1=(bij),则bji≤mjibii,j≠i.
引理6[10]设A=(aij)∈Rn×n,是严格对角占优M-矩阵,A-1=(bij),则bji≤vjibii,j≠i.
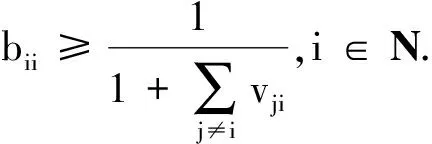
设A=(aij)是严格对角占优M-矩阵,A-1=(bij),易得mki≤ri,,于是vji≤mji.从而vi≤mi.
2 主要结果
文献[1-10]中分别给出了M-矩阵A与其逆矩阵A-1的Hadamard积的最小特征值τ(A°A-1)下界的一些结果.下面给出关于τ(A°A-1)的新下界:

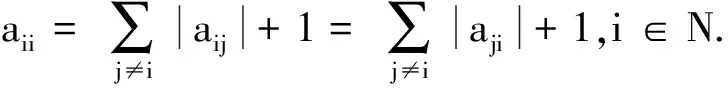
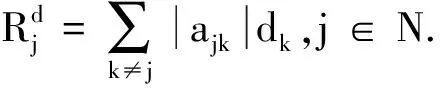
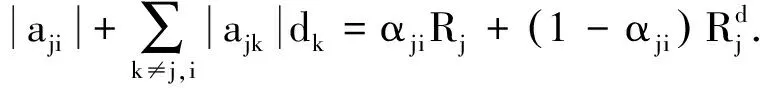

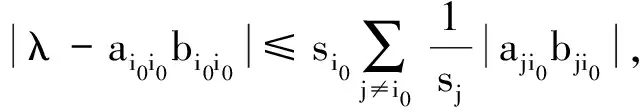
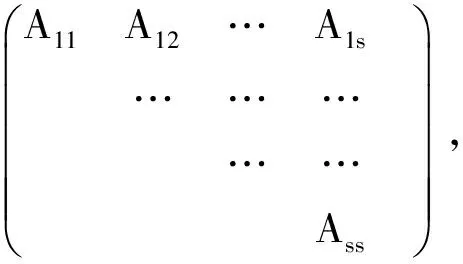
推论1 设A=(aij)∈Rn×n是严格对角占优M-矩阵,A-1=(bij)是双随机矩阵,则
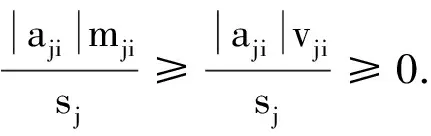
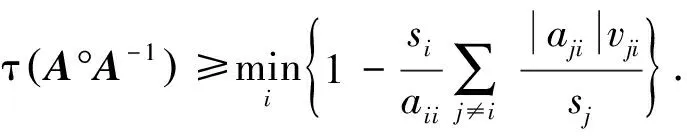
证明由定理1的证明和引理4知定理2成立.证毕

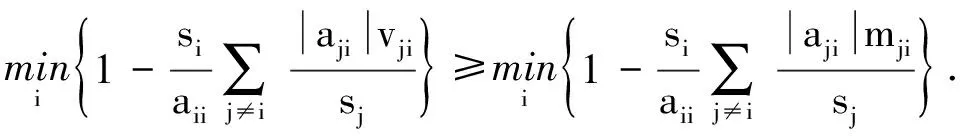
3 例子
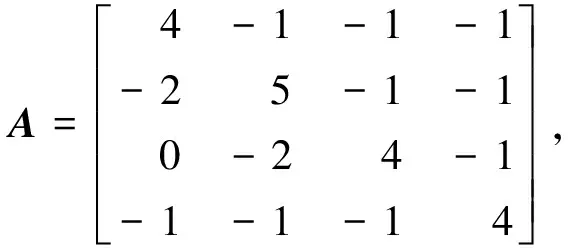

对τ(A°A-1)的下界进行估计:由文献[2-10]的结果分别得τ(A°A-1)≥0.500 0,τ(A°A-1)≥0.662 4,τ(A°A-1)≥0.799 9,τ(A°A-1)≥0.800 9,τ(A°A-1)≥0.8250,τ(A°A-1)≥0.825 0.由本文定理1得:τ(A°A-1)≥0.884 1;事实上τ(A°A-1)=0.975 5.以上表明,本文所得的结果改进了Feidler和Markham的猜想和文献[1-10]的结果.
4 结语
对M-矩阵与其逆的Hadamard积的最小特征值的下界进行了研究,得到了τ(A°A-1)的2个新下界.一方面,结果改进了文献[2-8]的结果.另一个方面,由数值算例表明本文所得的结果改进了文献[1-10]的结果.因此,所得的结果是对相关文献的一个有益补充.
参考文献:
[1] FIEDLER M, MARKHAM T L.An inequality for the Hadamard product of an M-matrix and inverse M-matrix [J].Linear Algebra Appl,1988,101:1-8.
[2] YONG Xue-rong, WANG Zheng.On a conjecture of fiedler and Markham [J].Linear Algebra Appl,1999,288:259-267.
[3] YONG Xue-rong.Proof of a conjecture of Fiedler and Markham [J].Linear Algebra Appl,2000,320:167-171.
[4] SONG Yong-zhong.On an inequality for the Hadamard product of an M-matrix and its inverse [J].Linear Algebra Appl,2000,305:99-105.
[5] CHEN Shen-can.A lower bound for minimum eigenvalue of the Hadamard product of matrices [J].Linear Algebra Appl,2004,378:159-166.
[6] LI Hou-biao,HUANG Ting-zhu, SHEN Shu-qian, et al.Lower bounds for the eigenvalue of Hadamard product of an M-matrix and its inverse[J].Linear Algebra Appl, 2007,420:235-247.
[7] LI Yao-tang,CHEN Fu-bin,WANG De-feng.New lower bounds on eigenvalue of the Hadamard product of an M-matrix and its inverse [J].Linear Algebra Appl, 2009, 430:1423-1431.
[8] 杨晓英,刘新.M-矩阵及其逆矩阵的Hadamard积最小特征值下界的估计 [J].山东大学学报:理学版,2012,47(8):64-67.
[9] 王峰.非奇异M-矩阵的逆矩阵和M-矩阵的Hadamard积的最小特征值下界估计[J].山东大学学报:理学版,2013,48(6):30-33.
[10] 高美平.M-矩阵与其逆的Hadamard积的最小特征值下界新的估计式[J].四川师范大学学报:自然科学版,2014,37(1):90-97.
[11] 黄廷祝,杨传胜.特殊矩阵分析及应用 [M].北京:科学技术出版社,2003:3-87.
[12] VARGA R S.Minimal Gerschgorin sets [J].Pacific J Math, 1965,15(2):719-729.
