改进型遗传算法求解TSP问题
2014-03-26石利平
石利平
(广东女子职业技术学院 应用设计系,广东 广州 511450)
旅行商问题(traveling salesman problem,TSP)[1]又译为货郎担问题,是求解一个闭合的最短路径问题。TSP问题可描述为单一旅行商由一个城市出发,通过给定的要去n个城市,已知各城市间的路程,路经每个城市仅1次,最后返回起始城市的最小路径问题,TSP是NP-Complete问题。生活中的车辆调度、生产线上螺母、城市管道铺设优化等优化问题,均属于TSP最短路径问题,研究如何求解TSP最优问题有着重要的实际意义。
遗传算法(genetic algorithm,GA)是一种著名的智能优化算法,是现代人工智能领域中的关键技术,大量科学实践也证明遗传算法在求解TSP问题方面具有比较高的寻优能力[2]。遗传算法全局寻优能力较强,使用较简单,采用概率化的搜索技术,搜索方向可以自适应地调整,能自动选择优化的搜索空间。但是遗传算法局部搜索能力较差,易出现早收敛和局部最小等问题[3]。本文提出一种基于精英保留选择策略和自适应选择变异算子,在选择、交叉、变异后再引入单向进化逆转操作的改进的遗传算法,提高遗传算法的搜索和求解性能。
1 TSP问题描述
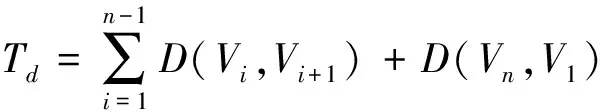
2 标准遗传算法
1975年遗传算法[3-4]由美国教授Holland提出。遗传算法是模拟“物竞天择,适者生存”以及基因遗传学的生物进化过程的随机化搜索方法。遗传算法是以种群个体适应度函数值作为搜索信息,搜索范围为种群所有的个体。
标准遗传算法(SGA)其基本流程[2-9]如下:首先构建初始种群,种群由一定数量的所求问题可能解个体组成,然后计算种群各个个体适应度函数值,经过遗传算法的3种重要操作算子选择、交叉和变异的多次处理,最终求出最优解。
3 改进的遗传算法
3.1 编码
本算法中采用整数排列编码。在TSP优化问题中,有n座城市,各城市的编号分别为整数1,2,3,…,n,这样一个染色体就由为n段组成。如TSP问题中有10个城市,那么{1,3,4,2,6,9,10,8,5,7}就是一个合法的染色体,也是一个可能的优化解。
3.2 初始化种群
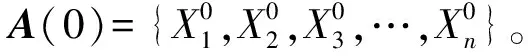
3.3 适应度函数
种群个体进化后是不是较优秀的问题解,即看其适应性,测评的标准就是适应度函数的值。适应度函数的值是群体进化过程中个体优胜劣汰唯一依据。个体适应度函数值较大,则说明该个体生存竞争能力较强,被选择进化的可能性高;反之,个体适应度函数值较小,则其个体生存能力较弱,在群体的进化中被淘汰的可能性高。适应度函数可以说是群体进化中的自然生存环境,是模拟生物界进化中优胜劣汰的自然选择[10]。因此在遗传算法中,如何合理设计适应度函数是非常重要的。本文中个体的适应度函数为
(1)
式中的D(Vi,Vi+1)表示城市Vi至城市Vi+1的距离,Ri表示第i条路径。
该适应度函数值是恰好走完n座城市再回到起始城市的距离倒数。染色体优化的目标就是选取尽量大的适应度函数值,适应度函数值越大则染色体越优。
3.4 选择操作
选择操作是以一定的选择概率从当前种群中选择适应函数值高的生成的新个体,其主要目的尽量使优质基因遗传给下一代,提高算法计算效率和全局收敛的概率。本文算法个体选择概率计算方法如下:
对于给定的规模为n的群体Q(n)=(q1,q2,q3,…,qn),个体qi的适应度函数值为F(qi),其选择概率为
(2)
本文算法在选择操作中加入精英保留策略[6,11]:即为在每代种群中加入一个适应度值大的精英个体,此个体为目前种群最好的个体;种群个体经过变异、交叉进化,若进化后的新一代种群中最好个体优于精英个体,则用最好个体替换精英个体,否则保留此精英个体。这种选择精英策略会保证父代种群中好的个体不会由于变异或交叉而丢失,子代种群中的最优个体永好于父代种群最优个体差。
3.5 交叉操作
交叉是很重要的操作算子,目的是将选择得到的优质个体进行交叉得到更优质新个体。交叉概率取值范围一般建议0.4~0.99[9]。
本文采用精英个体与选择后得的新个体进行部分映射杂交操作,交叉的位置随机产生,即随机产生交叉区域。假设城市数为10,交叉操作算法如下:
(1) 选择父代种群最优个体与一新个体;
(2) 随机产生2个交叉位置n1和n2,n1∈[1,10],n2∈[1,10],对这2个位置中间的数据进行交叉操作;
(3) 交叉后产生的新个体城市编号如有重复,采用部分映射方法消除重复,不重复的编号保留。
这种交叉方法可确保较大可能地保护好父代个体中的优质基因模式,从而使优质染色体遗传到下一代当中,有利于提高遗传算法的性能。
3.6 变异
变异操作是遗传算法的重要操作之一,是将问题解编码串中的某些位的编码与该解中其他位编码调换位置,形成一新个体。变异操作决定遗传算法的局部搜索能力,维持群体的多样性,避免早熟现象出现。遗传算法中,常以变异概率Pm对个体基因进行突变来实现产生新个体。为确保种群进化的稳定性,变异概率一般取较小值。种群进化后期,群体最优个体的适应度值与种群平均适应度值很接近,此时个体基因块也都非常相似,如果算法变异概率依然保持不变,那么遗传进化过程中个体间竞争性就会大大减弱,种群个体进化速度降低,种群多样性变弱,易造成局部收敛。为减少这种情况发生,本文采用一种自适应的变异概率[8-9]计算方法:
(3)
式3中Pm-max为最大变异概率,本文中取0.05;Pm-min为最小变异概率,这里取0.001,F为要变异个体的适应度,Fmax为种群中最大的适应度值,Favg为当前种群平均适应度值。
使用公式(3)选取变异概率时,当个体的适应度大于或等于此时种群的平均适应度时,该个体的变异概率就越小,则该个体发生变异的可能性越小,这样可更好地保证适应度高的优质个体遗传下去。当个体的适应度小于种群的平均适应度时,则其变异概率大,使其进化为优质个体可能性更大,这种思想与优胜劣汰的遗传机制一致。
本文中变异操作是随机产生2个变异位置n1和n2,n1∈[1,10],n2∈[1,10],将这2个位置对换,比如n1=3,n2=8,个体{1,3,4,2,6,9,10,8,5,7,}变异后得到新个体为{1,3,8,2,6,9,10,4,5,7}。
3.7 进化逆转操作
进化逆转操作能改善遗传算法的局部搜索能力。在选择、交叉、变异遗传进化之后引入进化逆转操作。逆转算法如下:先随机产生2个随机整数n1和n2(n1∈[1,10],n2∈[1,10]),确定2个位置,将TSP可能解路径排列中对应的城市交换位置,假如n1=2,n2=5,逆转后TSP环游路线排列{V1,V8,V6,V3,V2,V5,V7,V10,V4,V9},计算新个体的适应度值,如其适应度值优于逆转前的,则保留该新个体,否则保留原来个体。进化逆转后,适应度值提高的个体才接受下来,否则保留原个体。本算法中逆转是单方向的,只接受向好的适应度逆转。设有10座城市,一个TSP可能解路径排列为{V1,V2,V3,V6,V8,V5,V7,V10,V4,V9}。主要代码如下:
SelPath=PathL(D,Selch) %计算被选个体的路径长度,D为各城市的距离矩阵
InvCh=SelCh; % Selch是选择要逆转的个体
%InvCh是逆转后的个体
for i=1:row
pos1=randsrc(1,1,[1:col]);
pos2=randsrc(1,1,[1:col]);
mininv=min([pos1 pos2]);
maxinv=max([pos1 pos2]);
InvCh(i,mininv:maxin)=InvCh(i,maxinv:-1:mininv);
end
InvPath=PathL(D,InvCh);%计算逆转后路径长度
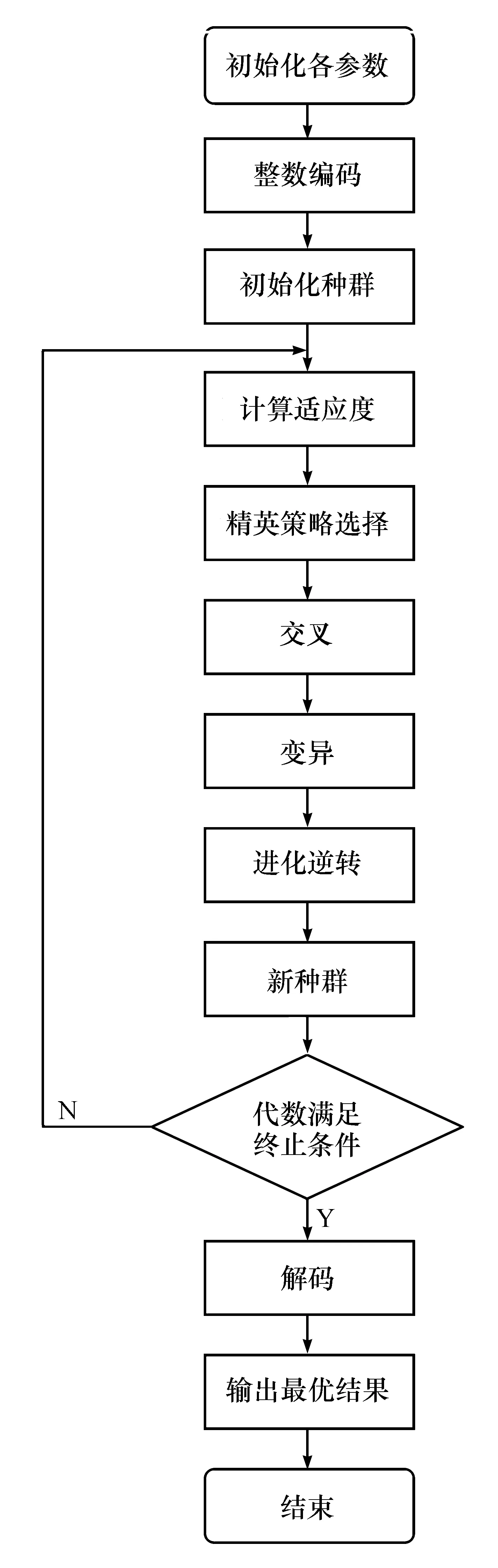
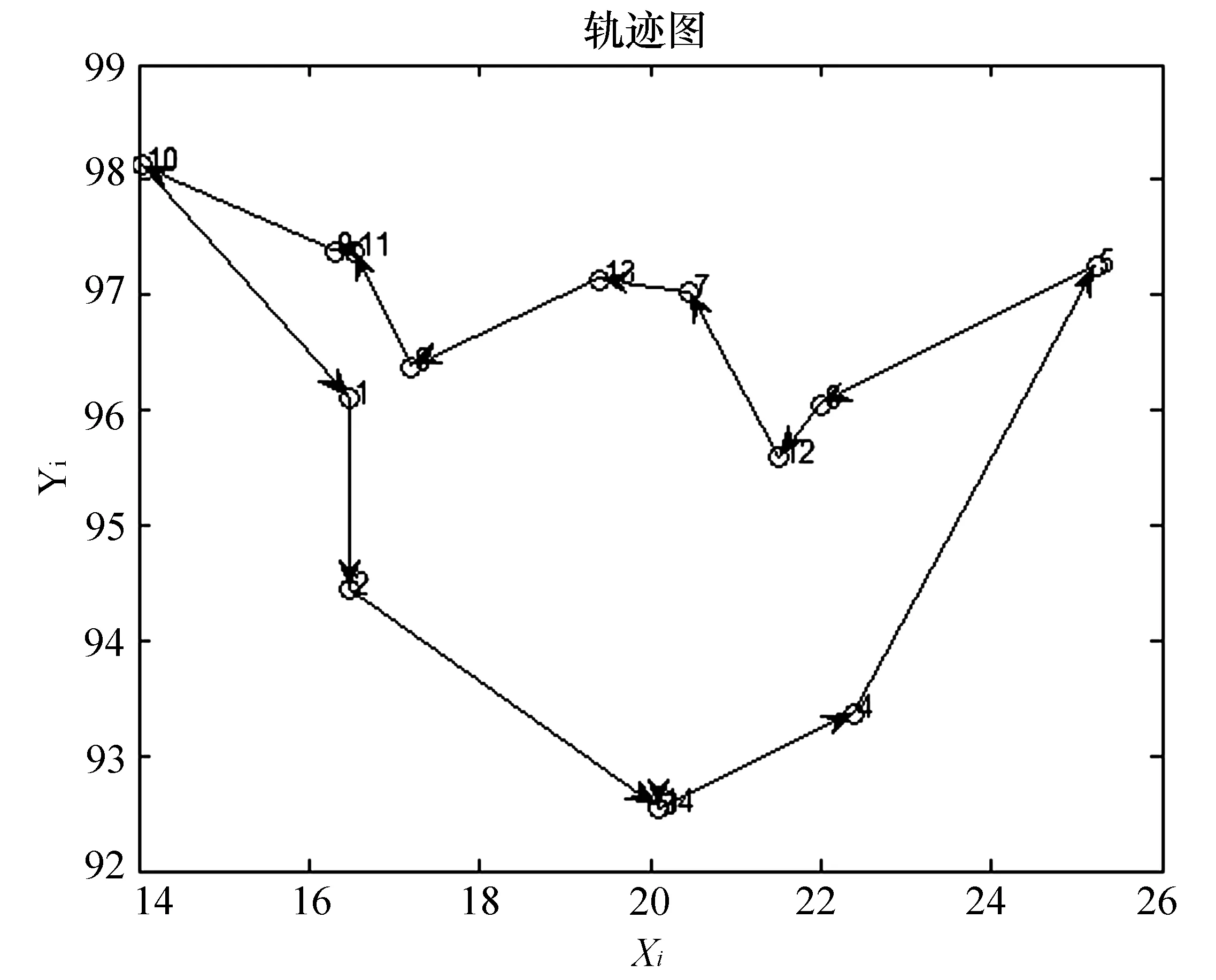
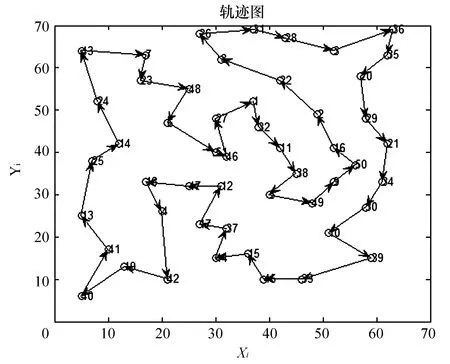
index=InvPath SelCh(index,:)= InvCh (index,:); 改进的遗传算法流程图如图1所示。 图1 改进的遗传算法流程图 本文选用国际上通用的TSPLIB测试库中数据的Barma14和Eli51数据进行测试。barma14数据的14个城市坐标如下: (16.47,96.10),(16.47,94.44),(20.09,92.54),(22.39,93.37),( 25.23,97.24),(22.00,96.05),(20.47,97.02),(17.20,96.38),(16.30,97.38),(14.05,98.12),(16.53,97.38),( 21.52,95.59),(19.41,97.13),( 20.09,92.55)。 Eli5数据的51个城市坐标如下: (37,52)(49,49)(52,64)(20,26)(40,30)(21,47)(17,63)(31,62)(52,33)(51,21)(42,41)(31,32)(5,25)(12,42)(36,16)(52,41)(27,23)(17,33)(13,13)(57,58)(62,42)(42,57)(16,57)(8,52)(7,38)(27,68)(30,48)(43,67)(58,48)(58,27)(37,69)(38,46)(46,10)(61,33)(62,63)(63,69)(32,22)(45,35)(59,15)(5,6)(10,17)(21,10)(5,64)(30,15)(39,10)(32,39)(25,32)(25,55)(48,28)(56,37)(30,40)。 分别使用标准遗传算法和本文中改进算法对TSP问题进行求解,两种算法基本参数一致,各重复执行20次,仿真结果如表1所示。 表1 遗传算法运行结果比较 从表1的仿真结果可知,本文算法求最优解的能力明显强于SGA算法。当TSP问题中城市数较少时,本文算法每次都能找到最优解;当城市数较多时,本文算法能找到近似最优解,求得的近似最优解比SGA算法求的近似最优解更接近于TSPLB所提供的最优解。本文算法求得两种数据下的最优路径分别如图2和图3所示。 图2 改进算法求解barma14最优解轨道 图3 改进算法求解Eli51最优解 通过对遗传算法对选择算子的改进,引入了精英保留策略,使优质个体在进化后尽最大可能保留;在变异操作中采用一种自适应算法选择变异算子,提高变异质量和算法的搜索效果。在选择、交叉、变异后再引入单向进化逆转操作,使子代继承亲代优质基因机会提高,提高算法搜索最优解的能力。仿真结果表明,优化后的遗传算法搜索最优解能力提高,且收敛快。但此算法也存在一定的局限性,当TSP问题的规模比较大,算法一般只能求解最优解的近似解。以后研究方向是将优化的遗传算法与其他算法相结合,如粒子群算法、模拟退火等算法[7,11],使TSP城市数比较大时,也能求出接近的最优解。 [1] Dorado M,Manifesto V,Colonic A.Ant system:optimization by a colony of cooperating gents[J].IEEE Transactions on Systems,Man,and Cybernetics-Part B,1996,26(1):29-41. [2] 马永杰,云文霞.遗传算法研究进展[J].计算机应用研究,2012,29(4):1201-1206. [3] Holland J H.Adaptation in natural and artificial systems [M].Ann Author: University of Michigan Press,Ml,1975. [4] Simians M,Pataki L M.Genetic Algorithms: A Survey[J].IEEE Computer,1994,27(6):17-26. [5] 赵明,宋晓宇,董洁,等.利用遗传算法求解应急物资调度优化问题[J].沈阳建筑大学学报:自然科学版,2012,28(5):944-948. [6] 刘全,王晓燕,傅启明,等.双精英协同进化遗传算法[J].软件学报,2012(4):765-775. [7] 王银年,葛洪伟.求解TSP问题的改进模拟退火遗传算法[J].计算机工程与应用,2012,23(4):765 -775. [8] 李晶皎,赵越,王骄,等.自适应记忆遗传算法研究[EB/OL].[2013-11-20].http://www.cnki.net/kcms/detail/61.1450.TP.20131129.1020.052.html. [9] 曹道友.基于改进遗传算法的应用研究[D].合肥:安徽大学,2010:13-14. [10] 傅颖勋.遗传算法的研究与改进[D].北京:北京邮电大学,2010:5-7. [11] 贾建芳,杨瑞峰,王莉.混合遗传粒子群优化算法的研究[J].自动化仪表,2013,34(9):1-3.4 解决TSP问题优化的遗传算法流程
5 仿真实验及结果

6 结束语
