肋片强化矩形截面螺旋通道换热特性研究
2014-03-26陈瑞杰马中元王兴斗刘晓宇李雅侠
陈瑞杰, 马中元, 王兴斗, 刘晓宇, 刘 刚, 李雅侠
(1.沈阳化工大学 能源与动力工程学院, 辽宁 沈阳 110142; 2.天津化工厂天泰化工公司, 天津 300480)
螺旋管道在化工、能源动力、制冷等工业的传热和分离设备中应用广泛.大量学者致力于螺旋通道内流体流动与换热及其强化传热特性研究[1-2].但目前大多数研究仍集中在圆形截面螺旋管道的研究,而对矩形截面螺旋管道的研究较少.邢云绯[3]采用数值模拟方法研究了矩形截面螺旋通道内流体湍流流动与换热特性,结果表明:由于螺旋管道曲率作用产生的二次流能够很好地强化矩形截面螺旋通道的换热,而且窄高型的(即高度大于宽度)矩形螺旋通道的强化换热效果更为显著.然而,张丽[4]通过采用实验结合数值模拟方法,研究矩形截面螺旋通道内流体流动特性,结果表明:高宽比越大,矩形横截面中心处的二次流强度越弱,并指出要强化矩形截面螺旋通道的换热应从改善换热面中心处的流动效果入手.
目前采用肋片强化换热的方法应用广泛.一方面肋片可以增加换热面积,另一方面肋片有助于使流体产生径向流动,产生附加二次流动,从而加强流体混合,促进管内流体速度和温度分布均匀,从而提高换热效果[5].目前肋片的强化换热方法已安全、经济地应用在各种换热设备上[6].签于此,本文提出在窄高型的矩形截面螺旋通道换热面中心线上安装螺旋纵向肋片,以进一步强化其内换热.给出了增加肋片后的螺旋通道内流场与温度场分布,研究了肋片高度对矩形截面螺旋通道的强化换热效果.
1 物理模型
对于精细化工领域的反应釜,在传统夹套内增加螺旋折流板后,可以使夹套内流场分布均匀,起到减少流动短路和死区,提高传热效果的作用,如图1(a)所示.此时由螺旋折流板以及内外筒体构成的通道可认为是窄高型的矩形截面螺旋通道,如图1(b)所示.当及时移除反应釜内的反应热确保产品质量是主要目的时,如何提高此类换热设备的换热能力具有重要的实际意义.通常折流板焊接在高温内筒壁面上,外部筒体布置保温材料.因此,可认为矩形截面螺旋通道的内壁面和上下壁面为恒定高温壁面;外壁面为绝热壁面,如图1(c)所示.
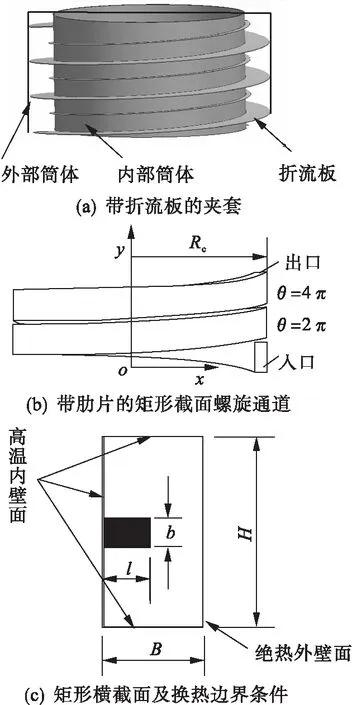
图1 物理模型及换热边界条件
图1中Rc为螺旋半径,B和H分别为矩形截面的宽度和高度,l和b为肋片的高度和宽度.为了研究肋片高度对矩形截面螺旋通道的强化换热效果,分别采用三种肋片高度,研究其对矩形截面螺旋通道的强化换热作用,即肋片高度分别为l=B/4、B/2和3B/4.螺旋通道结构参数及肋片参数如表1所示.螺旋通道选为2圈结构,即θ=4π,导流片厚度取为3 mm.肋片材料为铜.

表1 矩形截面螺旋管道及肋片结构参数
2 数值计算方法及数据处理
应用CFD软件FLuent,以水为工作介质进行数值模拟.文献[7]中指出:流体在弯曲通道湍流流动与换热时,由于湍流的脉动和螺旋流动的相互作用,表现出较高的各向异性和对流线弯曲的敏感性,可以采用Realizablek-ε模型.
入口采用均匀速度和均匀温度入口的边界条件(入口温度设定为288 K,高温壁面为393 K).出口采用充分发展出口边界条件.采用Quick格式离散动量方程、能量方程,离散方程的求解用修正速度压力的SIMPLEC方法.壁面采用无滑移壁面条件.各方程收敛条件为平均参差绝对值小于1.0×10-5.计算网格采用六面体网格,通过网格独立性实验消除了网格对计算精度的影响.
为了验证计算结果的准确性,用此数值模拟方法,计算了与文献[8]中实验结构相同的矩形截面弯曲管道换热平均努塞尔数Nu,数值模拟结果与实验结果的偏差小于10 %,证明此计算方法是可靠的.
定义雷诺数Re、阻力系数f和努塞尔数Nu如下:
(1)
(2)
(3)

(4)
(5)
其中:Q为换热量,J;A=πRc(H+2B+2l)为总换热面积,m2;tw为壁面温度,K;tin和tout分别为螺旋管中流体进出口温度,K;qm为质量流量.
3 结果与分析
3.1 流场
文献[4]中指出:流体在单一螺旋通道内流动与换热时,由于离心力的作用,在与主流方向垂直的横截面上会有二次流动产生,而且二次流仅在正交螺旋坐标系下可以获得.根据文献[4]中直角坐标系和正交螺旋坐标系的变换关系,得到正交螺旋坐标系下,θ=3π的横截面上无量纲轴向速度的等值线和二次流矢量图,如图2所示.

从左到右分别为l=0、B/4、B/2和3B/4,左侧为绝热外壁侧
图2Re=5 000时的流场
Fig.2 Flow fields atRe=5 000
从图2中可以看出:湍流条件下,单一矩形截面螺旋通道内(l=0时),二次流为旋转方向相反的两涡结构,二次流的涡心在远离换热壁面中心线的上下两侧.由于二次流的作用,横截面上无量纲轴向速度的最大值偏向外壁侧,同时外壁侧的轴向速度梯度大于内壁侧的速度梯度.
增加扰流肋片后,通道横截面上的二次流形状发生了较大的改变.由于肋片的扰动作用,产生了附加二次涡,随着肋片高度的增加,附加二次涡的范围增大,并逐渐靠近换热壁面.研究结果表明:二次流能够破坏边界层,强化换热.因此,在矩形截面螺旋通道内增加扰流肋片后,附加的二次涡会进一步强化换热.从图2(b)中也可以看出,增加肋片后,横截面上无量纲轴向速度分布也发生了较大变化,随着肋片高度的增加,无量纲轴向速度的最大值位置由一个变为两个,最大值也逐渐增大.
3.2 温度场
定义无量纲温度Θ为:
(6)
图3给出了θ=3π的横截面上,无量纲温度Θ的等值线,从图中可以看出,随着肋片长度的增加,换热壁面上温度分布越来越均匀,说明换热效果增强.
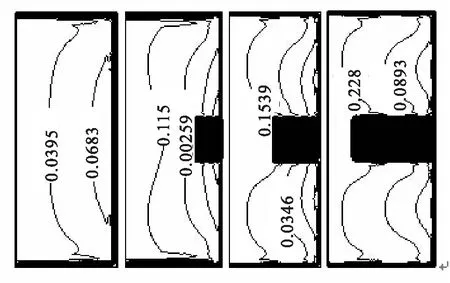
从左到右分别为l=0、B/4、B/2和3B/4,左侧为绝热外壁侧
图3Re=5 000时的无量纲温度场
Fig.3 Temperature fields atRe=5 000
3.3 强化换热及阻力特性
3.3.1 单一螺旋通道换热壁面Nulocal分布
图4给出了θ=3π的横截面上,单一矩形截面螺旋通道内换热壁面上局部努塞尔数Nulocal的分布曲线.
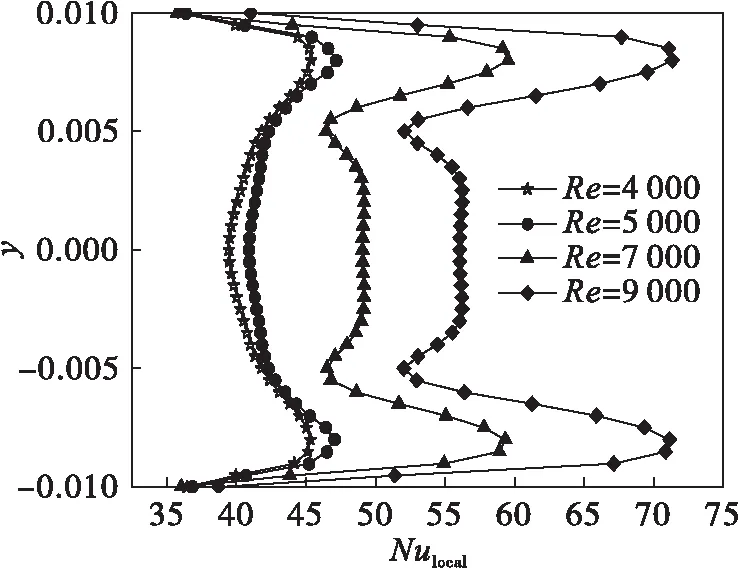
图4 单一螺旋通道内换热壁面Nulocal分布曲线
由图4可以明显看出:换热壁面中心线附近,即y=0位置Nulocal值明显小于两侧的Nulocal值.这主要是由于二次流涡心远离此处,对换热效果影响较小的缘故.因此,采取措施强化此处换热会提高矩形截面螺旋通道的换热效果.
3.3.2 肋片的强化换热效果分析
图5和图6给出了不同肋片高度下,对流换热系数α和流动阻力系数f随雷诺数Re的变化曲线.
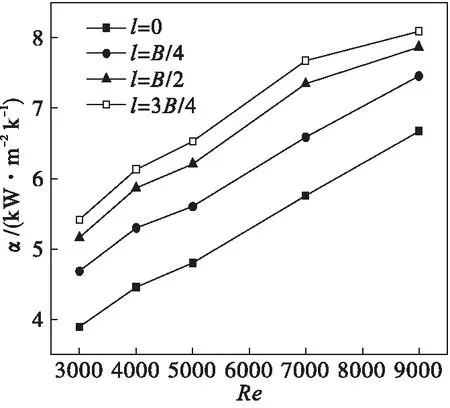
图5 不同肋片高度下的对流换热系数α

图6 不同肋片高度下的流动阻力系数f
从图5、图6中可以看出:随着肋片高度l的增加,矩形截面螺旋通道内对流换热系数α和流动阻力系数f均增大.这是由于附加二次流一方面能够破坏边界层,对换热起强化作用,另一方面二次涡增大了壁面附近流体的速度梯度,即增大了流动阻力.分析计算结果表明:加装肋片后的α是单一矩形截面螺旋管道的1.03~1.2倍,而f为1.003~1.033倍.综合传热和流动两方面因素来分析肋片对矩形截面螺旋通道的强化换热效果,定义强化换热因子j为:
(7)
式中Nu0和f0分别为单一矩形截面螺旋通道内流体换热平均努塞尔数和阻力系数,Nu和f分别为加入肋片后的对应值.图7给出了不同高度的扰流肋片强化矩形截面螺旋通道换热时,强化换热因子j随雷诺数Re的变化曲线.从图7中可以看出:强化换热因子j在0.911~1.067之间,说明强化传热具有意义.随着雷诺数Re的增加,j均减小,说明肋片较适合强化低雷诺数下的矩形截面螺旋通道换热.从图7中还可以看出:随着肋片高度的增加,j值逐渐减小,这说明肋片高度增加带来的换热量提高程度弱于肋片高度增加导致的流动阻力增加.这是由于随着肋片高度增加,附加的二次涡逐渐远离换热内壁面,对换热的相对强化作用减弱.
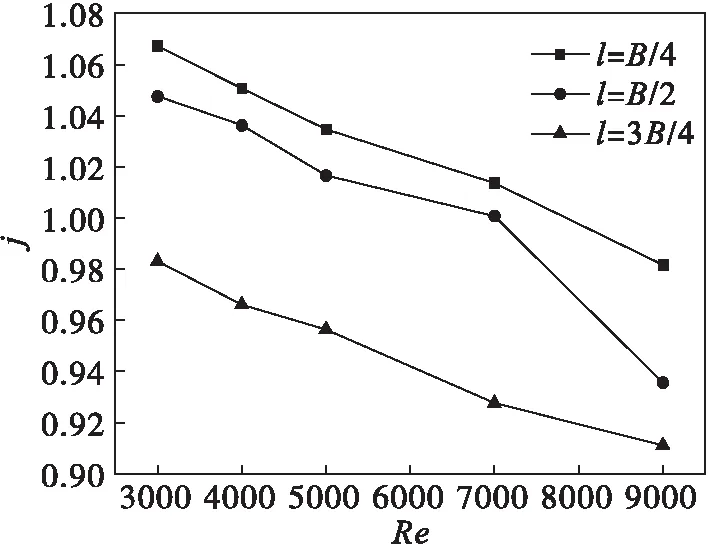
图7 强化换热因子变化曲线
4 结 论
采用计算流体力学软件Fluent研究了肋片对矩形截面螺旋通道的强化换热作用.速度场和温度场分析结果表明:在矩形截面螺旋通道换热面中心线增加扰流肋片后会产生附加的二次涡,使得对流换热系数和流动阻力系数同时增加.低雷诺数下肋片的综合强化换热效果要好于高雷诺数下的强化换热效果.研究范围内,加装肋片后的对流换热系数α是未加装肋片的1.03~1.2倍,流动阻力系数f是未加装肋片的1.003~1.033倍;强化传热因子j在0.911~1.067之间.
参考文献:
[1] Jayakumara J S,Mahajani S M,Mandala J C.CFD Analysis of Single-phase Flows Inside Helically Coiled Tubes[J].Computers and Chemical Engineering,2010,34:430-446.
[2] 湛含辉,朱辉.螺旋管内迪恩涡运动的数值模拟[J].热能动力工程,2011,26(1):41-47.
[3] 邢云绯,仲峰泉,张新宇.矩形横截面螺旋管内湍流流动与换热特性[J].航空学报,2013,34(6):1269-1276.
[4] 张丽,邢艳伟,吴剑华,等.矩形截面螺旋通道内流体流动特性[J].化工学报,2010,61(5):1089-1096.
[5] 李清芳,张国忠,林媛媛,等.内肋套管管内流动与换热特性研究[J].工程热物理学报,2009,30(12):2122-2124.
[6] 刘湘云,史保新,李克天,等.螺旋内肋管的流阻与换热特性实验研究[J].中北大学学报(自然科学版),2010,31(2):108-112.
[7] 陶文铨.数值传热学[M].2版.西安:西安交通大学出版社,2001:347-353.
[8] Mori Y,Uchida Y,Ukon T.Forced Convective Heat Transfer in a Curved Channel with a Square Cross Section[J].International Journal of Heat and Mass Transfer,1971,14(11):1787-1805.
