有源钳位推挽变换器控制策略的研究
2014-03-25朱景全
朱景全,李 媛
(商丘师范学院,河南 商丘 476000)
1 问题的提出
随着科技与社会的发展,人们对各种电气设备的要求也越来越高.推挽电路由于其简单的结构,被广泛引用于逆变器,UPS等诸多领域.然而由于开关管关断时,漏磁能量会在开关管上引起一个较大的电压尖峰,以及在能量传递的一个周期内功率器件开关变换馈能不平衡导致能量伏秒面积不等引起的变压器的偏磁问题[1]15-18,推挽电路的使用受到了一定的限制.随着有源钳位推挽变换器的提出,电压尖峰问题得到了很大的改善,经实验验证其能有效地解决常规变换器效率低下、变压器漏磁的问题[2]60-63.有源钳位推挽变换器拓扑结构图如图1所示:
本文针对有源钳位推挽变换器,使用基于PI调节的电压负反馈进行控制.这种控制方法实现简单,处理迅速,可以很好地控制有源钳位推挽变换器稳定工作,且有效地降低了漏磁能量在开关管上引起的电压尖峰.
2 有源钳位推挽变换器控制策略
2.1 推挽变换器的数学模型
由于PWM控制的推挽电路非线性很强,故而使用电路的动态特性来分析非常困难.一般对DC/DC变换器的建模方法主要有数字仿真法与解析建模法.数字仿真法使用数学算法求得DC/DC变换器中所需的数字解,虽然精度高,但不易与其电路意义联系起来[3].解析建模法使用解析表达式求解,虽然电路意义明确,但是使用困难.故此处选用状态空间平均法对推挽电路进行分析. 推挽变换器拓扑结构图如图2所示:

图1 有源钳位推挽变换器拓扑结构图

图2 推挽变换器拓扑结构图
状态平均法从DC/DC变换器的状态空间方程出发,通过平均、小信号扰动[4]53-55、线性化处理得到数学模型以及电路模型.这种方法电路意义明确,并且方便进行进一步的分析.
给推挽电路限定4个假设条件:变压器原边的两个开关管与副边的整流二极管均为理想开关;整流滤波器的频率远远低于开关管的开关频率;动态扰动信号的频率也远远低于开关管的开关频率;扰动信号的幅值远远低于稳态值.这样,就可以得到推挽电路的动态小信号模型,如图3所示,本文只讨论电感电流连续的情况[5]957-961.
对小信号模型使用状态空间平均法,得到推挽变换器的数学模型如式(1)、(2):
(1)

(2)
2.2 基于PI调节的电压负反馈控制策略
由推挽变换器的数学模型可得输出电压与输入电压之间的关系Vo=2ndVs.将脉冲宽度调制器的传递函数近似为一个比例系数为1/Vm的比例环节,使用电压反馈,且反馈系数设置为β.此电压负反馈的推挽变换器控制结构框图如图4所示:

图3 推挽电路的动态小信号模型

图4 推挽变换器的电压闭环控制结构框图
在闭环系统中添加比例积分(PI)环节,可以提高系统稳定性,保证系统精度,提高系统抗干扰能力.PI环节中的比例环节可以提高系统跟踪误差的快速性,同时积分环节可以降低系统误差.PI调节发展成熟,实现简单,调节好PI参数既可以保证系统稳态精度,又可以保证动态响应的迅速性.
PI环节的传递函数的一般模型式(3):
(3)
其中:Kp为PI环节的比例系数,Ti为PI环节的积分时间常数.
对于PI调节中的参数,Kp越大,系统响应速度越快,但是系统超调量也会增大,若此参数过大,则会引起系统的不稳定.积分环节的参数选取不当也会给系统稳定性,系统跟踪的快速性等带来不利的影响.故而要使PI调节器有效地工作,必须要合理地对PI参数进行整定.
在工程应用中通常使用二阶工程设计法来整定PI调节器的参数,并进行一定的优化.二阶工程设计法的基本思想是根据已知系统的被控对象传递函数,与所希望得到了系统开环传递函数进行对比,以此确定PI参数.
二阶系统的闭环传递函数一般如式(4):
(4)

(5)
令系统的开环传递函数为Φ0(s),则可得系统开环传递函数与闭环传递函数的关系如下:
Φ(s)=Φ0(s)/[1+Φ0(s)]
(6)
根据式(6)可得二阶系统的理想开环传递函数的表达式:
(7)
根据理想开环传递函数表达式,用二阶工程设计法的思想,设计出PI调节器的最优参数.
此经过优化的PI调节器不仅结构简单,精度高,稳定性好,而且对某些传感器或其他执行机构产生的延时做了弥补,使系统的输出能更快更好地跟踪给定信号.
3 仿真研究
根据上述的有源钳位推挽变换器的拓扑结构图,在simulink中搭建仿真模型如图5所示:
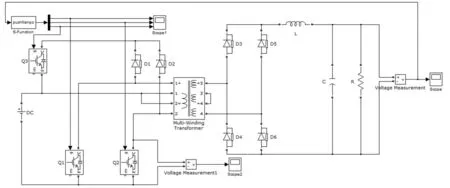
图5 有源钳位推挽变换器PI控制仿真模型
图中,Q1、Q2管为推挽电路的主开关管,Q3管为有源钳位管.输出电压反馈到控制单元,根据既定的控制策略向三个开关管发出PWM信号,控制其开通与关断以达到推挽升压同时去除开光管上的电压尖峰.
对该模型进行仿真分析,得开关管Q2两端电压如图6所示:
而对于普通推挽电路,Q2两端的电压波形如图7所示:

图6 有源钳位推挽变换器PI控制Q2管两端电压

图7 普通推挽变换器Q2管两端电压
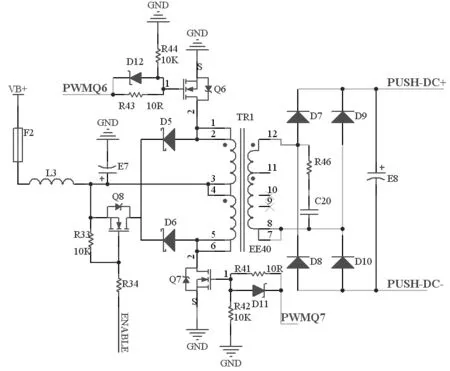
图8 有源钳位推挽变换器主电路图
由此可见,使用基于PI的电压负反馈控制的有源钳位推挽变换器可以有效地消除开关管Q1、Q2两端电压中的尖峰,保证了开关管的长期稳定运行.
4 实验研究
4.1 实验平台的构成
搭建有源钳位推挽升压变换器的主电路如图8所示:
其中,Q6、Q7作为推挽电路的两个开关管,二极管D5、D6以及Q8构成了有源钳位通路.二极管D7、D8、D9、D10作为整流二极管工作,电感L3与电容E7,E8分别构成了输入滤波电路与输出滤波电路.
电路工作时,蓄电池的电能经过输入滤波电路加到推挽变压器的3、4引脚上,Q6导通时,变压器原边向副边馈能.当Q6关断且Q7未导通时,Q8管导通,形成通路,给变压器的漏感放电.而在Q7导通时,给Q8施加关断信号,重复以上工作循环.
软件控制框图如下图9:

图9 有源钳位推挽变换器软件PI控制框图
4.2 实验结果及分析
使用上面搭建的实验平台进行实验,用示波器观测开关管Q7两端的电压,得出实验波形如图10:
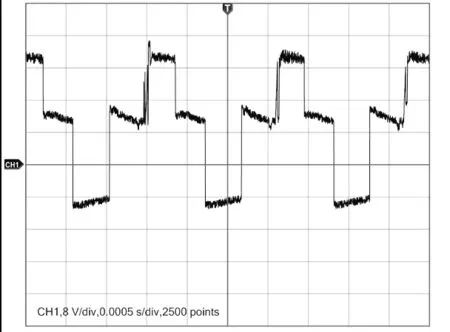
图10 示波器观察出的开关管Q7两端电压波形
5 结论
推挽变换器的应用越来越广泛,然而其漏感在开关管上引起的电压尖峰却限制了推挽变换器的发展.有源钳位推挽变换器则很好地弥补了这一点,与无源钳位电路将漏感中的能量通过电阻发热的形式吸收相比较,保证了系统的变换效率.本文通过对推挽变换器的数学模型进行分析,确立了基于PI调节的电压负反馈控制策略,结合二阶工程设计法对PI参数进行整定与优化,保证了系统稳定高效地运行.经过仿真与实验的验证,本文的控制策略可以有效地减小变压器漏感引起开光管电压尖峰,并使推挽变换器稳定可靠运行.
参考文献:
[1] 徐 田,鞠志忠.消除推挽DC/DC变换器偏磁策略的研究[J].通信电源技术,2008(05).
[2] 李康艺,王兴蔚.单输出有源钳位正激DCDC变换器设计[J].磁性材料及器件,2010(10).
[3] 刘三山.基于MPPT的离网光伏发电系统的设计[D].合肥:合肥工业大学,2013.
[4] 刘伟晗, 王 琪, 龚春英. 双环控制型推挽正激DC- DC变换器的小信号建模[J] . 电源世界, 2005(9).
[5] 张 兴,马先奎,张崇巍.推挽式DC、DC开关电源的设计与校正[J].合肥工业大学学报,2000(12).
