孤南地区浅层稠油弹性参数敏感性分析及应用

王振涛,董月昌,王玉梅

(1.中国石油化工股份有限公司胜利油田分公司物探研究院,山东东营257022;2.中国石油化工股份有限公司胜利油田分公司勘探处,山东东营257022)

胜利油田孤岛地区新近系和古近系馆陶组河流相储层中稠油储量丰富,呈环状围绕孤岛油田分布。随着勘探的不断深入,孤岛油田南区(以下简称“孤南地区”)分布的动用性差、采收率低的稠油藏成为挖潜增产的重要目标。孤南河流相储层砂体横向变化快、叠置关系复杂,油气受构造与岩性的双重控制,各小层油水系统自成一体,油水关系复杂,勘探成功率不高,钻井相对较少,井网控制程度差,砂体储层以及油水分布一直不落实。在地震储层预测方面,由于该区油藏岩石物理研究不够深入,对储层岩性和流体的敏感弹性参数认识不清,造成储层岩性及流体的预测精度低,多解性大,严重阻碍了勘探开发进程[1-3]。

在实验室测量中,稠油与水的弹性参数相当接近,易被误认为地层中饱和稠油岩石与饱和水岩石的岩石物理弹性参数特性相似,导致稠油层和水层难以识别。在有关稠油藏岩石物理研究方面,20世纪80年代Wang等[5]通过实验发现稠油和饱和油砂体随着油藏环境条件的变化而变化,并证实稠油未固结砂岩温度升高时纵波速度明显降低,饱和稠油岩石在地层条件和地面条件下岩石物理特性存在差异。

针对孤南地区浅层稠油藏地震流体预测问题,我们利用经验公式研究地层温度、压力以及水矿化度对稠油和地层水岩石物理参数的影响,估算地层条件下稠油和水的纵波速度、密度以及体积模量等岩石物理参数,在此基础上利用岩石物理横波估算和流体替换技术分析稠油藏岩性和流体敏感参数,通过叠前高精度反演获取包括泊松比和拉梅系数敏感参数在内的多种数据体,应用双参数油层概率判识技术识别含油层,以提高孤南地区浅层稠油藏的油层预测能力。

1 地层条件下流体体积模量估算

国内外油藏研究人员通过大量实验研究分析,形成了一系列估算原油和地层矿化水密度、速度的经验公式。地层压力和温度都会对原油密度产生影响,且石油组分不变时,两者的影响非常独立。原油密度受压力影响的经验公式为

(1)

式中：ρP为原油在压力P时的密度,g/cm3;ρ0为原油在15.6℃和一个大气压下所测得的原油密度,g/cm3;P为地层压力,MPa。原油密度随压力的增大而增大,孤南地区稠油藏埋深为1100～1500m,埋深较浅的地层压力相对低,统计为10～13MPa,地层压力对该区原油密度影响小。

原油密度受温度影响的经验公式为

(2)

式中：ρ为地层原油密度,g/cm3;T为地层温度,℃。ρ为地层原油密度,g/cm3。原油密度随着温度的升高而降低,孤南地区稠油藏温度为50～70℃,对原油密度影响大,估算地层原油密度为770～820kg/m3。

原油速度的计算利用Batzle等[6]提出的原油速度与压力和温度关系的经验公式:

(3)

式中：v为地层原油速度,m/s。原油速度随温度和压力的升高而升高,与实验室测量变化关系一致[7],估算孤南地区稠油藏地层原油速度为1397～1454m/s。

地层水弹性参数不仅受温度和压力的影响,而且也受到水矿化度的影响,Batzle等[6]利用实验结果建立了求取地层水密度和速度的经验公式：

式中：ρw为纯水密度,kg/m3;ρb为地层矿化水密度,kg/m3;vw和vb为纯水和地层矿化水速度,m/s;T为地层温度,℃;P为流体压力,MPa;S为地层水矿化度,mg/L;wij为常量。其中,根据实际资料设定,纯水密度ρw为1000kg/m3,地面原油密度ρ0取加热20℃测量平均值970kg/m3。孤南浅层油藏地层水矿化度变化大,水矿化程度高,统计为10000～18000mg/L,估算地层水密度为1076～1152kg/m3,地层水速度为1680～1700m/s,温度和矿化度对地层水速度和密度影响较大,两者随温度和矿化度的增大而增大,压力对地层水速度和密度影响较小。

对孤南地区浅层稠油和水的密度对比分析表明,在地面条件下稠油和纯水密度差异不大,纯水的密度稍高于重油的密度,而在地层条件下稠油与地层水密度差异明显,地层水密度比油的密度高达300kg/m3(图1)。对孤南地区浅层稠油和水的速度对比分析表明,在地面条件下稠油和纯水速度差异不大;而在地层条件下稠油与地层水速度差异明显,地层水速度比稠油速度高达270m/s(图2)。

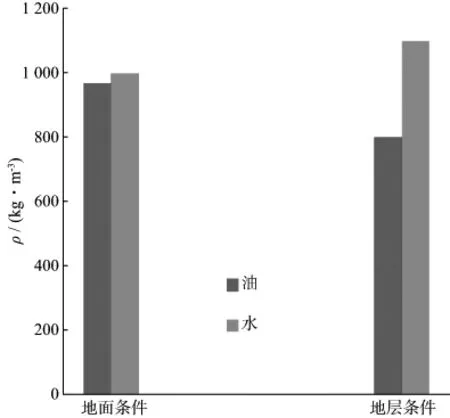
图1 地面和地层条件油、水密度对比

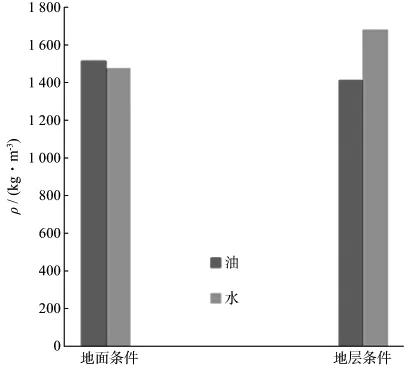
图2 地面和地层条件油、水纵波速度对比

利用估算出的流体速度和密度就可以计算稠油和水的体积模量,公式为

(7)

式中：K为体积模量,Pa;v为流体速度,m/s;ρ为流体密度,kg/m3。流体体积弹性模量与速度和密度成正比,地层稠油的密度和纵波速度分别低于地层水的密度和纵波速度,因此地层稠油体积模量也低于地层水体积模量。

对流体速度和密度取平均估算值,稠油速度和密度分别取1420m/s和800kg/m3,地层水速度和密度分别取1690m/s和1100kg/m3,得到孤南浅层稠油体积模量为1.6×109Pa,地层水的体积模量为3.1×109Pa。地层水体积模量约为稠油体积模量的两倍,稠油和地层水的体积模量差异明显,这是能够开展孤南稠油地震识别的岩石物理基础。

2 储层弹性参数敏感性分析

2.1 岩性敏感参数分析

地层弹性参数影响因素复杂,不仅受饱含流体的影响,而且受矿物组成、孔隙大小与形状以及胶结程度等多种因素的影响,在对地层中的流体识别之前首先应进行砂岩储层的识别。通过测井岩石物理横波估算以及多参数分析,确定区分砂岩储层与围岩的岩性敏感参数[8-14]。

饱和岩石纵波速度、横波速度以及密度是开展岩石物理参数计算分析的重要基础信息,纵波速度和密度测量成果多,但横波速度测量成果很少,所以需要根据已有测、录井信息进行横波估算。基于Gassmann饱和岩石模量估算理论以及岩石模量与速度、密度关系式,饱和岩石纵、横波速度计算方程为

式中：vP和vS分别为饱和岩石纵波速度和横波速度,m/s;Kf,Ks,Kd分别为流体、固体矿物和干岩石骨架体积模量,GPa;φ为孔隙度;μd为干岩石骨架剪切模量,GPa;ρe为饱和岩石密度,kg/m3。

横波速度估算过程主要包括：①基于含水饱和度和孔隙度等测井信息,结合油藏条件下稠油和地层矿化水纵波速度、密度参数,应用流体混合理论[15],得到混合流体弹性模量;②孤南浅层河流相储层主要矿物成分以石英、长石以及粘土矿物为主,基于固体矿物混合模型理论,得到主要矿物弹性模量;③利用测井曲线估算泥质含量,基于Xu-White模型,给出初始参数,得到初始岩石骨架弹性模量;④利用岩石物理理论模型正演模拟,得到饱和岩石纵波速度、横波速度与密度,并通过对比实测纵波速度和密度进行误差分析,如果误差大,修改不确定变量,直至误差最小可认为构建的岩石物理模型逼近实际地层,从而估算出可靠的饱和岩石纵波速度、横波速度和密度。

针对孤南地区稠油储层砂岩、泥岩的岩性识别,对纵波速度、横波速度和密度分别进行了单参数敏感性分析(图3)。由图3a可以看出,砂岩纵波速度整体高于泥岩纵波速度,但是泥岩速度值跨度大,两者叠置明显,用纵波速度难以识别砂岩和泥岩;砂岩横波速度(图3b)整体也高于泥岩横波速度,其对岩性的敏感程度高于纵波速度,但泥岩横波速度跨度也很大,叠置区域也很大,利用横波速度也不易区分砂岩和泥岩;孤南地区浅层稠油藏埋深浅,上覆地层压力相对小,砂岩压实脱水作用弱,总孔隙度大,而泥岩脱水压实作用强,孔隙度收缩明显,总孔隙度小,造成砂岩密度低于泥岩密度,含油后会更低,但砂岩、泥岩密度的统计频次中心接近(图3c),且地震中很难提取准确的密度信息,因此,不适合用密度来识别砂岩和泥岩岩性。

进一步利用纵波速度、横波速度和密度计算纵横波速度比、泊松比、拉梅系数、剪切模量等弹性参数并分别进行敏感性分析,综合对比认为,利用泊松比参数区分孤南地区稠油储层砂岩和泥岩,结果较为理想,从泊松比弹性参数统计分析结果(图3d)可以看出,砂岩低值而泥岩高值的特征明显,两者叠置区域相对较小,统计频次中心差异大。

图3 孤南地区稠油储层砂、泥岩弹性参数敏感性分析a 纵波速度vP; b 横波速度vS; c 密度ρ;d 泊松比σ

2.2 流体敏感参数分析

在岩性敏感参数分析的基础上,利用流体替换技术对储层流体弹性参数敏感性进行分析。选取GN209井深度1470m的砂岩储层(孔隙度φ为34%,含水饱和度Sw为42%),利用地层条件下稠油和水体积模量估算结果和流体替换技术,得到不同含流体状态下饱和砂岩对应的岩石物理弹性参数(表1)。

从表1中可以看出,砂岩横波速度vS随含水饱和度的增大而减小,但变化幅度很小;纵波速度vP和密度ρ随含水饱和度增大而增大,变化明显;纵横波速度比vP/vS、泊松比σ、拉梅系数λ等多种弹性参数也表现为随含水饱和度增大而增大的特征,且变化特征相对明显,其中拉梅系数对流体敏感性最强,可以优选作为孤南地区稠油储层流体识别的敏感弹性参数(图4)。

表1 特定砂岩储层流体替换的弹性参数变化

图4 孤南地区稠油储层流体弹性参数敏感性分析

3 敏感弹性参数反演及应用

岩性和流体弹性参数敏感性分析认为,泊松比对砂岩储层的岩性识别较为敏感,而拉梅系数对储层中流体的变化较为敏感。在根据低泊松比参数对砂岩储层识别的基础上,利用低拉梅系数可以较好地预测识别砂岩含油性。

叠前反演是目前比较成熟的地层弹性参数求取技术,它利用叠前分角度叠加数据,通过初始模型约束控制,获得纵波速度、横波速度和密度,从而计算出纵横波速度比、泊松比以及拉梅系数等多种地层弹性参数[16]。目前大多数叠前反演方法通常采用Zoeppritz方程的简化近似公式,但会存在两个方面的问题,一是在上、下地层参数变化大的情况下,近似式反演会产生一定的计算误差;二是在大角度反演计算时,误差也会较大。

孤南地区稠油藏埋深小于1500m,地震资料采集面元为25m×50m,入射角度能够达到36°,资料频宽为6～65Hz,主频35Hz左右,地震资料品质相对较好。但是由于入射角度大,基于Zoeppritz方程近似式的叠前反演方法反演精度低。因此,我们采用叠前高精度反演方法,对Zoeppritz方程直接求解构建叠前反演Jacobi偏导数矩阵方程[17-18],建立反射系数与纵波速度、横波速度和介质密度的关系,实现了基于Zoeppritz方程反射系数梯度矩阵的弹性参数精确计算。利用该方法得到的储层泊松比和拉梅系数体准确性更高,为稠油层识别提供了较好的属性参数。

利用双参数概率判识技术[19]对反演得到的泊松比和拉梅系数体开展油层识别。将研究地层划分为含油砂体、含水砂体以及围岩3种主要岩相,不同岩相在泊松比-拉梅系数交会图上具有不同的分布区域(图5);利用测井岩石物理分析获得的泊松比和拉梅系数统计信息,分别建立3种岩相的双参数概率密度分布函数和先验概率函数,利用概率判识技术得到油层分布概率体,预测孤南地区稠油藏的油层分布情况。

图5 孤南地区稠油储层不同岩相的泊松比-拉梅系数交会分析

结合钻井资料对油层分布概率体进行分析，结果表明,稠油藏的油层识别精确度大大提高,多解性进一步降低。GN202井在深度1191～1198m钻遇单层厚7m的油层,试油期间产油4.6t/d,产水20.1t/d,综合含水81%;GNX209井在深度1469～1479m内钻遇两层厚8m的油层,试油期间产油6.8t/d,产水5.4t/d,综合含水44%。从油层分布概率预测剖面(图6)上看,GN202井稠油储层段表现为中等含油概率特征,而GNX209井稠油储层段表现为高含油概率特征,预测结果与试油结果吻合。同时,钻遇的非含油储层和围岩在图6 上都表现为低含油概率特征,预测结果与钻井吻合程度高。

利用三维镂空技术对预测的中、高含油概率砂体进行了解释,图7为预测的孤南地区稠油藏油层厚度平面分布,从整体面貌上可以看出，该地区河道砂体储层纵、横向变化快,油水关系复杂。由图7 可见,GNX209,GNX204,GNX210,GN202,GN218C,K72和K103等多口井钻遇的含油砂体展布清楚,而临近的K54,K57,GN218,GN8和GN17井没有钻遇油层,为失利井,预测结果与钻井吻合程度高。

图6 孤南地区稠油层分布的泊松比和拉梅系数双参数概率预测剖面

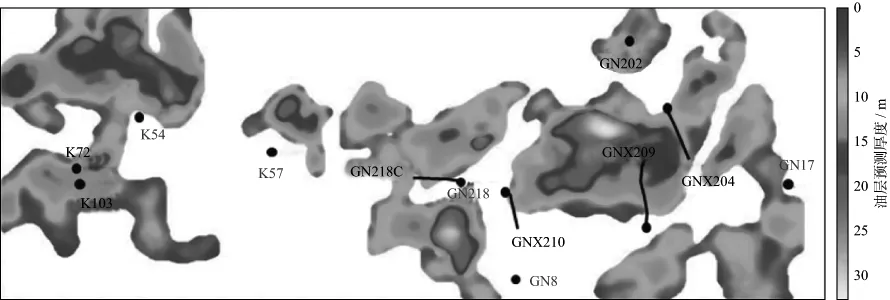
图7 孤南地区浅层稠油藏油层预测厚度平面分布

4 结束语

孤岛油田南区浅层稠油藏埋深浅,压实差,孔隙度大,流体弹性参数差异对饱和岩石的体积模量有较显著的影响,地层条件下饱含油砂体与饱含水砂体弹性参数特征差异明显,具有稠油识别的岩石物理基础。在测井横波估算和岩性敏感参数分析的基础上,再利用流体替换技术对储层流体弹性参数进行了敏感性分析,表明利用低泊松比可以很好地区分出砂岩储层,利用低拉梅系数可以很好地识别砂岩储层中的含油层。利用叠前高精度反演方法精确提取地层弹性参数信息,对反演得到的泊松比和拉梅系数进行双参数油层概率判识,最终得到的油层分布概率体可以较好地进行孤南地区稠油藏油层预测。地震岩石物理综合研究及应用的成果表明,基于岩石物理分析和叠前高精度反演的双参数油层概率判识技术提高了孤南地区浅层稠油藏的油层识别能力,降低了稠油藏地震流体识别的多解性。

参 考 文 献

[1] 王忠.孤岛油田馆陶组含油层系多源供烃判识及成藏分析[J].天然气地球科学,2011,22(3)：391-398

Wang Z.Oil Sources in multi-directions and accumulation analysis in Guantao Formation of Gudao Oilfield in Zhanhua Sag[J].Natural Gas Geoscience,2011,22(3)：391-398

[2] 束青林,张本华,徐守余.孤岛油田河道砂储集层油藏动态模型及剩余油研究[J].石油学报,2005,26(3)：64-73

Shu Q L,Zhang B H,Xu S Y.Dynamic model and remaining oil distribution of fluvial reservoir in Gudao Oilfield[J].Acta Petrolei Sinica,2005,26(3)：64-73

[3] 王学忠,王建勇.孤东油田地热采油可行性研究[J].断块油气田,2008,15(1):126-128

Wang X Z,Wang J Y.Study on feasibility of geothermal oil recovery in Gudong Oilfield[J].Fault-Block Oil & Gas Field,2008,15(1):126-128

[4] 毕俊凤,顾汉明,刘书会,等.河道砂体地震响应特征及影响因素分析——以垦东1地区馆陶组上段河道砂为例[J].石油物探,2013,52(1):97-103

Bi J F,Gu H M,Liu S H,et al.Analysis on seismic response characteristics of channel sands and its influence factors:case study of Upper Guantao Formation in KD1 area[J].Geophysical Prospecting for Petroleum,2013,52(1):97-103

[5] Wang Z,Nur A,Batzle M.Acoustic velocities in petroleum oil[J].Journal of Petroleum Technology (SPE18163),1988,571-585

[6] Batzle M,Wang Z.Seismic properties of pore fluids[J].Geophysics,1992,57(11):1396-1408

[7] 马中高,伍向阳.石油流体弹性参数实验研究[J].石油物探,2007,46(1):94-99

Ma Z G,Wu X Y.Experimental study on elastic properties of oil[J].Geophysical Prospecting for Petroleum,2007,46(1):94-99

[8] 王玉梅,苗永康,孟先军.岩石物理横波速度曲线计算技术[J].油气地质与采收率,2006,42(5)：535-538

Wang Y M,Miao Y K,Meng X J.Calculation procedure of shear velocity curve on petrophysics[J].Petroleum Geology and Recovery Efficiency,2006,42(5)：535-538

[9] 郝前勇,印兴耀,王玉梅,等.弹性模量流体因子在永新工区储层预测中的应用[J].石油物探,2012,51(5):502-507

Hao Q Y,Yin X Y,Wang Y M,et al.Application of elastic modulus fluid factor on reservoir prediction at Yongxin Block[J].Geophysical Prospecting for Petroleum,2012,51(5):502-507

[10] 李燕,刘浩杰,王玉梅.Gassmann模型机理分析及其应用[J].勘探地球物理进展,2010,33(1):16-20

Li Y,Liu H J,Wang Y M.Mechanism analysis of Gassmann model and its application[J].Progress in Exploration Geophysics,2010,33(1):16-20

[11] 张元中,周开金,赵建斌,等.砂泥岩地层横波测井曲线预测方法研究[J].石油物探,2012,51(5):508-514

Zhang Y Z,Zhou K J,Zhao J B,et al.Shear-wave logging curve prediction method for shaly sand formation[J].Geophysical Prospecting for Petroleum,2012,51(5):508-514

[12] Xu S,White R E.A new velocity model for clay-sand mixtures[J].Geophysical Prospecting,1995,43(1):91-118

[13] Xu S,White R E.A physical model for shear-wave velocity prediction[J].Geophysical Prospecting,1996,44(4):687-717

[14] Keys R G,Xu S Y.An approximation for the Xu-White velocity model[J].Geophysics,2002,67(5):1406-1414

[15] 张金强,马中高,曲寿利,等.碳酸盐岩储层流体替换中混相流体体积模量的计算[J].石油物探,2012,51(2):133-137

Zhang J Q,Ma Z G,Qu S L,et al.Calculation of bulk modulus for mixed-phase fluid in fluid substitution for carbonate reservoir[J].Geophysical Prospecting for Petroleum,2012,51(2):133-137

[16] 高云,朱应科,赵华,等.叠前同时反演技术在砂砾岩体有效储层预测中的应用[J].石油物探,2013,52(2):223-228

Gao Y,Zhu Y K,Zhao H,et al.Application of prestack simultaneous inversion technique in effective reservoir prediction of sand-gravel body[J].Geophysical Prospecting for Petroleum,2013,52(2):223-228

[17] 刘福平,孟宪军.反演纵横波速度的Jacobian矩阵及精确计算方法[J].中国科学：地球科学,2010,40(11)：1608-1616

Liu F P,Meng X J.Jacobian matrix for the inversion of P- and S-wave velocities and its accurate computation method[J].China Science:Earth Science,2010,40(11)：1608-1616

[18] 孟宪军,刘福平.地震反射系数的相角变化[J].石油地球物理勘探,2010,45(增刊1)：121-124.

Meng X J,Liu F P.The phase angle change for seismic reflection coefficient[J].Oil Geophysical Prospecting,2010,45(S1)：121-124

[19] 王振涛,王玉梅,钮学民.贝叶斯判别方法在叠前反演数据解释中的应用[J].海洋地质前沿,2012,28(3)：67-72

Wang Z T,Wang Y M,Niu X M.Application of Bayes criterion to interpretation of prestacking simultaneous inversion[J].Marine Geology Frontiers,2012,28(3)：67-72