基于时频域谱模拟的时变子波估计方法

张漫漫，戴永寿，张亚南，丁进杰，王蓉蓉

(中国石油大学(华东)信息与控制工程学院,山东东营257061)

地震波在地下介质传播过程中，由于地层的吸收和滤波作用，子波能量逐渐被吸收，高频成分逐渐衰减，因此待估计的子波具有动态衰减性。为了满足油气勘探的需要，得到高分辨率的地震资料，时变子波的提取成为地球物理工作者一个重要的研究方向。

时变子波估计方法很多，如胡启宇[1]和Liang等[2]使用同态理论和高阶统计量估算时变和空变地震子波;彭才等[3-4]提出了基于动态褶积模型的子波估计方法;Baan[5]提出了基于峰值最大化的时变地震子波估算方法;高静怀等[6]基于反射地震记录变子波模型提取地震子波进而提高地震记录分辨率;冯晅等[7]提出分时窗提取地震子波的方法并应用于合成地震记录中。这些方法大都采用分段处理，即首先对地震记录在时间上进行分段，假设每段内的地震子波是时不变的，进而在每段内提取出一个时不变的地震子波。受分段长度的影响，每段提取的平均意义子波与实际子波势必存在一定误差，使得后续的地震资料处理和解释结果不准确。当相邻地层的地震反射振幅和频率成分差异比较大时，分段提取的方法将不能很好的反映相邻层段中子波的变化。

为了突破地震记录平稳性假设，解决上述常规分段子波提取方法存在的局限性和不足，本文考虑到地震记录中由于地层的吸收滤波作用导致的地震波振幅和高频成分衰减的情况，提出了一种基于时频谱模拟的时变子波估计方法。

1 基于时频域谱模拟的时变子波估计方法

首先对地震记录做时频分析，在二维时间-频率域内进行滤波处理，然后采用谱模拟的方法拟合出每一反射点处的子波振幅谱(这里假设地震记录已经过零相位化处理)，从而实现时变子波的提取，其处理流程如图1所示。该方法不需要考虑对子波进行衰减补偿，与分段子波提取方法相比，摒弃了分段平稳的假设，更精细地刻画了地震记录中的非平稳成分。

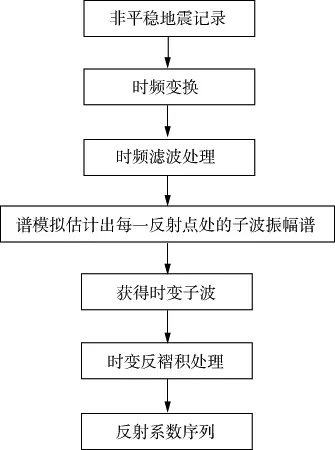
图1 基于时频域谱模拟的时变子波估计方法流程

1.1 地震记录的时频分析

实际地下介质是粘弹性的，地震子波在地下介质中传播时由于波前扩散和吸收衰减等效应会使子波能量衰减、频带变窄，所以地震子波随时间变化，记录的地震资料是一个非平稳信号。而时频分析是研究非平稳信号的有力工具，它以联合时频分布的形式来表示信号的特性，可以较为准确地定位某一时刻出现的频率分量。所以，对地震记录进行时频分析能够充分显示出其中的非平稳特性。

常用的时频分析方法有短时傅里叶变换、Gabor变换、小波变换和S变换等。其中，S变换是在继承短时傅里叶变换和小波变换优点的同时，克服了短时傅里叶变换时频分辨率不变以及小波变换的尺度因子与频率无关的缺点。S变换采用与频率有关的可变高斯窗函数，其窗函数定义如下：

(1)

式中：f为频率。可以看出，S变换窗函数的变化趋势固定不变，不能根据实际需要灵活调整，为此很多学者对S变换的窗函数加以改进提出了多种广义S变换[8-10]。常用的广义S变换采用时窗宽度随频率f呈反比例变化的高斯窗函数。在高频段时窗较窄，可获得较高的时间分辨率;在低频段时窗较宽，可获得较高的频率分辨率。这些广义S变换对于大多数非平稳信号能获得较好的时频效果，但仍不能很好满足非平稳地震记录处理所要求的分辨率。齐春燕等[11]在广义S变换的基础上提出一种改进的广义S变换，其窗函数的表达式为

(2)

式中：q,p为大于零的调节因子。从(2)式可以看出窗函数的宽度与频率呈正比例变化，即在低频处可获得较高的时间分辨率，在高频处获得较高的频率分辨率，此性质符合地震记录动态衰减特性。信号s(t)的时频谱为

(3)

利用该方法对地震记录进行时频分析，可获得更高的时频分辨率，且具有很好的时频聚焦性，能够有效地分辨出地震资料中频率成分的变化，有利于更精细地分析地层结构。此外，该方法还可进行无能量损失的反变换，从而准确重构时间域地震信号。

1.2 地震记录时频谱的时频滤波

由上述可知，改进的广义S变换具有良好的时频聚焦性，能够获得高质量的时频谱信息，在压制噪声、判断反射层的位置以及油气的直接显示等方面可获得较好的应用。然而受测不准原理的限制，我们不可能同时获得较高的时间分辨率和频率分辨率[12]。由文献[13]可知，对所获得的非平稳地震记录的时频谱直接处理，有一定效果，但不是很理想。为了更好的适应薄互层的地震分析和解释，在保持现有频率分辨率的同时尽可能提高时间分辨率，避免相邻反射地层之间的影响，引入一种时频滤波器[14]对地震记录的时频谱进行滤波处理。该滤波器应是时间和频率的光滑函数，且具有以下特性：

1) 对某一时间τ，当t=τ时，H(t,ω)=1;当|t-τ|→∞时，H(t,ω)=0;

2) 对某一时间ξ，当ω=ξ时，H(t,ω)=1;当|ω-ξ|→∞时，H(t,ω)=0。

即H(t,ω)对空间点(τ,ξ)具有时频局域化性质。据此定义如下形式的3参数(λ,p,v)时频滤波器：

(4)

函数的后一部分对前一部分起衰减控制作用，不同的λ,p对应不同的衰减。λ越小，p越大，H(t,ω)越尖锐，支集越小，实际应用中一般λ取负值，p取正值。取λ=-1,p=1,v=2时的时频滤波器的三维曲面图如图2所示。

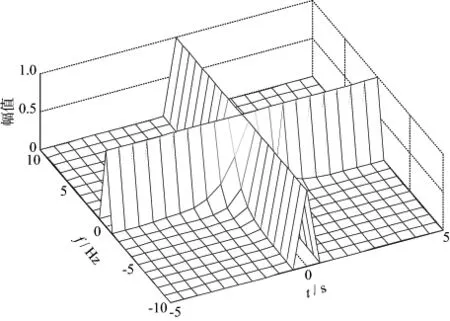
图2 时频滤波器的三维曲面表示

利用上述滤波器对地震记录的时频谱进行滤波：

(5)

f≠0

式中：S(τ,f)为处理后的地震记录时频谱;T为时频滤波器的时窗宽度;tr为反射系数出现的时间点，且T/2小于相邻反射系数最小间隔的一半。

1.3 基于时频域谱模拟的时变子波提取

得到地震记录的时频谱后，需要从中拟合出子波的时变振幅谱。常用的方法是在反射系数是白噪序列的假设条件下，通过地震记录的自相关得到子波振幅谱。然而实际的反射系数序列并不一定符合白噪假设，且自相关法不能用于时频域提取时变子波，为此本文提出采用谱模拟[15]的方法估计时变子波。该方法一般用于反褶积处理中[13,16-17]，是一种比较有效且稳健性较强的地震子波模拟方法。

谱模拟假设地震子波的振幅谱是平滑的，认为子波振幅谱类似于雷克子波谱的单峰光滑曲线，对其在频率域进行数学建模，数学表达式为

(6)

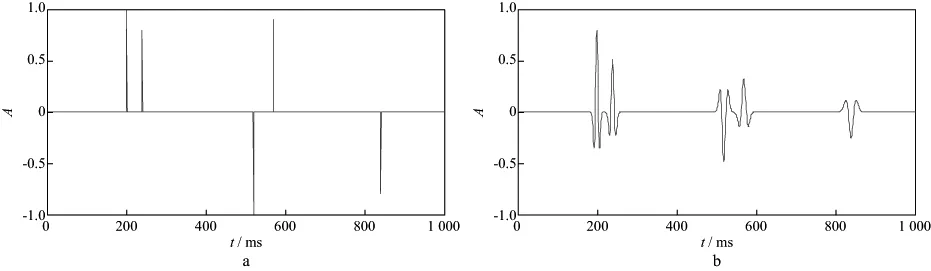
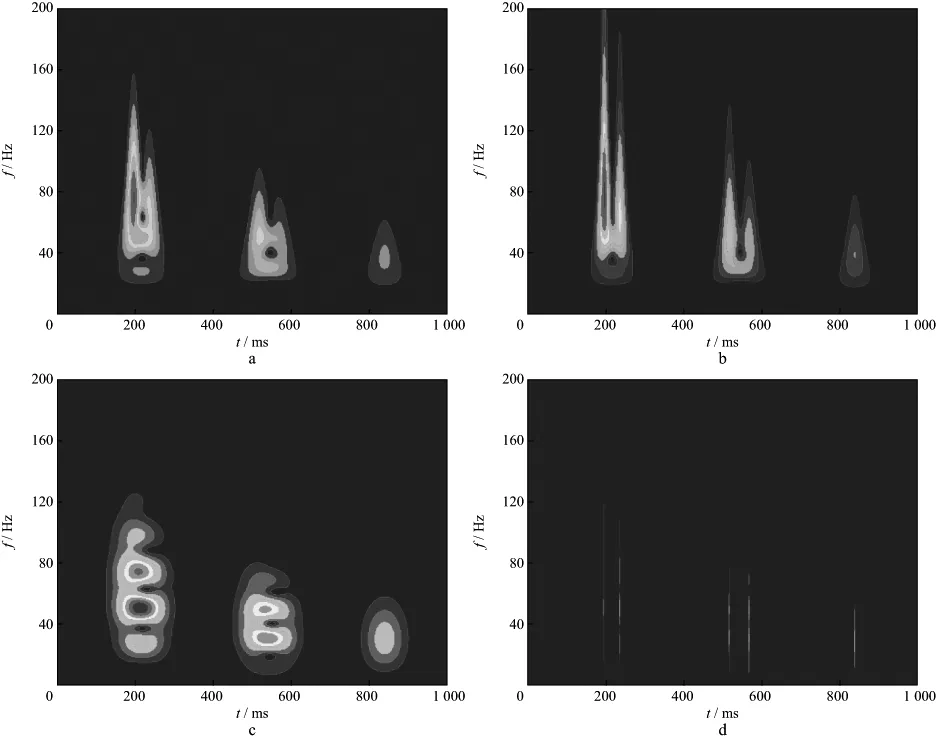
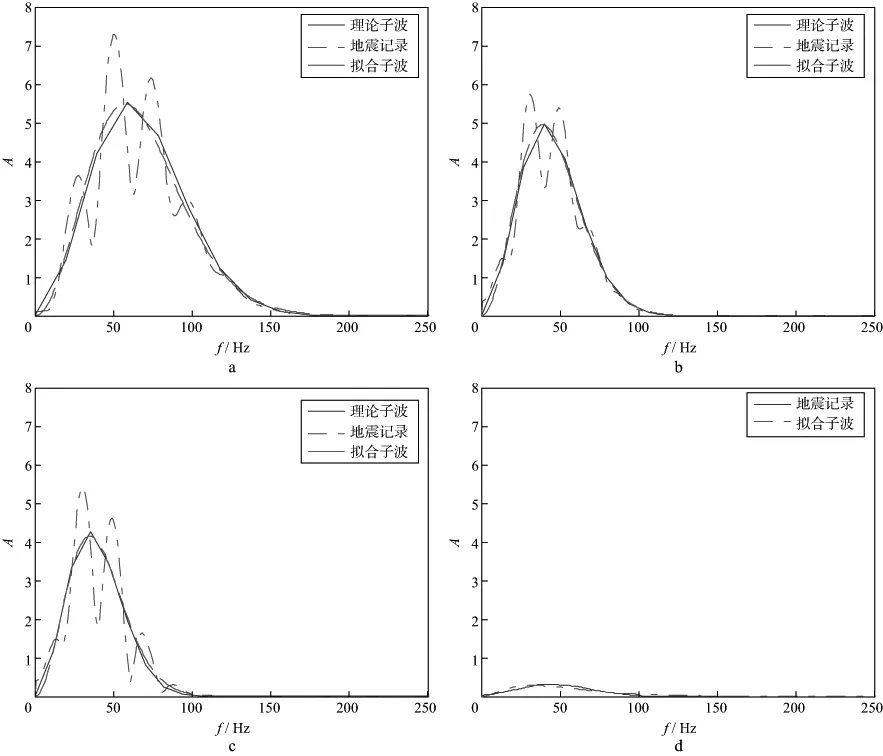
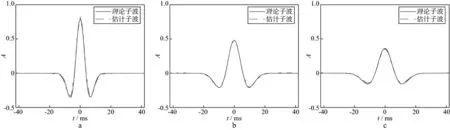
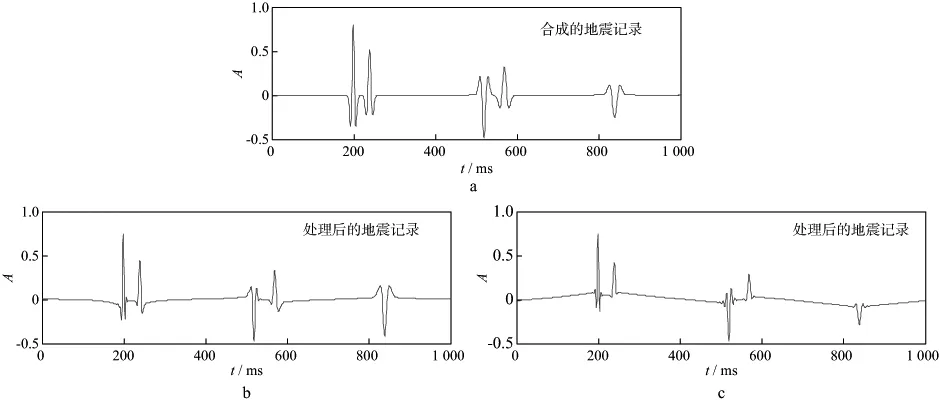
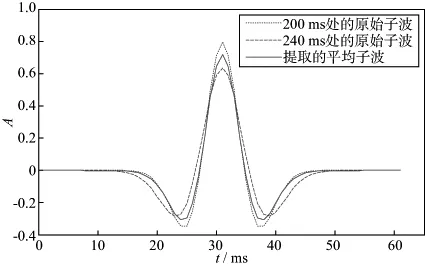
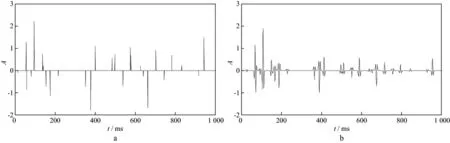
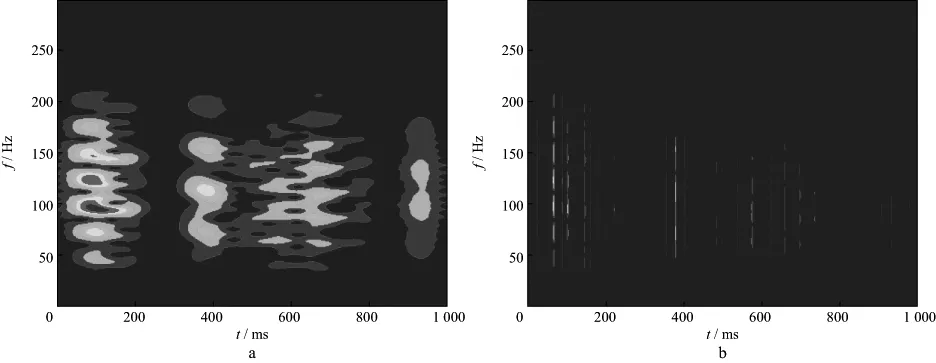
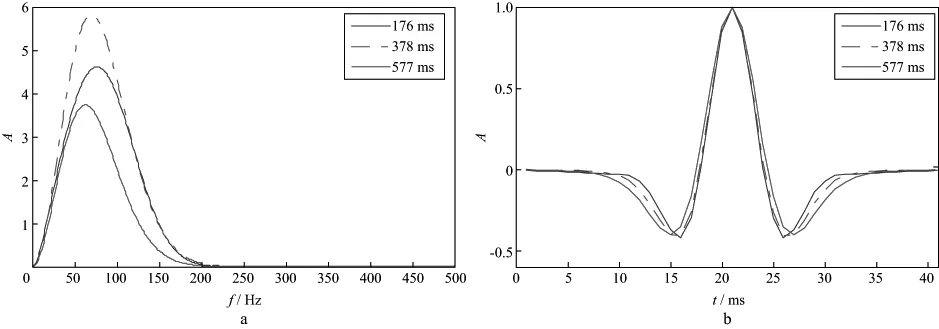
式中：k是一个常数;N为阶数;an是关于f的多项式系数，一般0

基于时频域谱模拟的时变子波估计方法具体实现过程：

1) 对地震记录x(t)进行改进的广义S变换，得到相应的时频谱SNGST(τ,f);

2) 对地震记录的时频谱进行时频滤波处理，得到处理后的时频谱S(τ,f)。

3) 固定时间T，提取相应时刻的地震记录频谱S(T,f)，通过谱模拟的方法拟合出该时刻的地震子波振幅谱W(T,f)，根据实际需要对相位进行处理(本文假设子波已通过零相位化处理)，反傅里叶变换即可得到该时刻的地震子波。

根据地震记录中反射点出现的不同位置，改变时间τ的取值，可实现时变子波的精细提取。子波提取的最终目的是进行反褶积处理，在去除子波影响时，采用时变维纳滤波法[5]进行反褶积处理，从而提高了地震记录的处理精度。

2 数值模拟

我们采用含有5个反射系数脉冲的稀疏模型进行试验，其长度为1000ms，采样频率为1ms，如图3a所示。各反射系数脉冲的位置和大小分别为(200ms,1.0)，(240ms,0.8)，(520ms,-1.0)，(570ms,0.9)和(840ms,-0.8)，其中包括2个相邻的同向反射系数和2个相邻的异向反射系数。采用主频分别为60,50，40，35，30Hz且振幅逐渐衰减的零相位雷克子波与反射系数序列褶积得到逐渐衰减的合成地震记录，如图3b所示。

图3 反射系数序列(a)和逐渐衰减的合成地震记录(b)

图4是对上述合成地震记录进行多种时频分析的结果。从图4可以看出，与S变换和广义S变换相比，改进的广义S变换具有更好的时频分辨率，且能准确地反应出相邻2个地层的频率成分及其差异。然而，从改进的广义S变换谱可看出，虽然原反射系数出现的时间点200，240，520，570，840ms处的能量最大，但在邻域内仍存在频率成分，这会对后续子波估计进而去除子波成分有一定的影响。图4d是对改进的广义S变换谱滤波后的结果，可以看出，在保持频率分辨率的同时，获得了更好的时间分辨率。

从处理后的地震记录时频谱中，分别提取每个时刻的地震子波。图5分别为200，520，570，650ms时的原始理论子波的振幅谱、地震记录的振幅谱以及模拟出的子波振幅谱对比结果。图6分别为200，520，570ms处的原始理论子波与估计子波时域对比结果。

图4 S变换(a)、广义S变换(b)、改进的广义S变换(c)以及滤波后的时频谱(d)

由图5和图6可以看出：①模拟出的子波振幅谱与原始子波振幅谱基本吻合，反变换到时域亦是如此，从而证明谱模拟提取时变子波振幅谱的准确性;②对比520ms和570ms处的模拟结果，相邻地层之间虽然存在相互影响，但本文提出的方法仍能准确的提取出每一反射点处的子波;③随着时间的增加，拟合出的子波其主频逐渐降低且能量减少，能够反应出子波在传播过程中的动态衰减特性;④提取反射点以外时间点处的子波(如图5d)，虽然能得到一个振幅谱，但其主频较原始子波有一定误差，且能量很低。

用得到的时变子波对地震记录进行动态反褶积处理，结果如图7所示。可以看出，用时频域谱模拟提取的时变子波进行反褶积处理后的地震记录，消弱了子波的影响。对比图7中滤波前、后的处理效果，可以明显看出，滤波处理后的反褶积结果在反射点处更加接近脉冲。

图5 200ms(a)，520ms(b)，570ms(c)，650ms(d)时理论子波、地震记录和拟合子波的振幅谱对比

图6 200ms(a)，520ms(b)，570ms(c)时的原始子波与估计子波时域对比

图7 用估计子波作动态反褶积处理后的地震记录a 原始合成记录; b 处理后记录(无滤波); c 处理后记录(加滤波)

若采用分段处理的方法提取子波，200和240ms,520和570ms很可能被分到一个时段内。图8是200和240ms所在段内提取的平均子波，可以看出，该子波与两个时刻的原始子波均有一定的误差，而用此子波进行反褶积处理结果必然不准确。

为了进一步说明问题，合成一个比较接近实际的非平稳地震记录。随机生成一个稀疏反射系数利用本文方法处理该非平稳地震记录，图10a显示了对地震记录进行改进的广义S变换得到的时频谱，图10b是时频滤波处理后的结果，可见，处理后的时频谱在频率分辨率不变的基础上，其时间分辨率大大提高，这有利于后续的地震资料处理。仅以176，378，577ms为例，图11a为拟合出的子波振幅谱，图11b为反变换回时域后的归一化子波。从3个时刻的图形对比不难看出，随着时间的增加，子波主频逐渐降低，频带变窄，相应时域波形变宽，说明本文方法能够很好地反映地震记录中的非平稳成分，准确精细地提取出时变子波。由于378ms处的反射系数较大，模拟的378ms处的子波振幅谱的幅值比176ms处的大，但其主频仍是降低的。

序列(图9a)，对应的非平稳地震记录为图9b。

图8 分段提取子波对比

图9 反射系数序列(a)和非平稳合成地震记录(b)

图10 对非平稳合成地震记录进行广义S变换(a)及滤波后的结果(b)

图11 不同时刻子波提取对比a 子波振幅谱; b 时域子波

提取出每一反射点处的子波后，将其用于反褶积处理，得到提高分辨率后的地震记录(图12)，从处理前、后地震记录的对比可以很明显的看出，反褶积处理后的地震记录上在反射点处更接近脉冲序列，从而说明本文方法能够准确提取时变子波，有效提高地震资料分辨率。

图12 用提取子波作反褶积处理前(a)、后(b)地震记录对比

3 结束语

常用的时变子波提取方法大都采用分段提取，当相邻层段的子波属性存在较大变化时，分段方法不能有效地反应这一变化。为此，我们研究提出了一种基于时频域谱模拟的时变子波提取方法。理论分析和数值模拟结果表明，该方法有效刻画了地震记录中的非平稳成分，且不需要对反射系数序列进行白噪假设;时频滤波器的引入大大提高了时间分辨率，能够更精细地提取出时变子波;在提高地震资料分辨率方面，该方法不需要研究地震记录的动态衰减机制，直接对地震资料进行处理，避免了误差累积。

本文提出的方法在实际应用中的稳定性和普适性等问题，有待后续在对实际地震资料的处理中作进一步探讨。

参 考 文 献

[1] 胡启宇.同态反褶积的一种可能途径[J].石油物探,1984,23(2):109-111

Hu Q Y.A possible way for hommorphic deconvolution [J].Geophysical Prospecting for Petroleum,1984,23(2):109-111

[2] Liang G H,Cai X P,Li Q Y.Using high-order cumulants to extrapolate spatially variant seismic wavelets [J].Geophysics,2002,67(6):1869-1876

[3] 彭才,朱仕军,黄中玉,等.基于动态褶积模型的动态子波估计[J].石油物探,2007,46(4):224-328

Peng C,Zhu S J,Huang Z Y,et al.Dynamic wavelet estimation based on the dynamic convolution model [J].Geophysical Prospecting for Petroleum,2007,46(4):224-328

[4] 彭才,曾涛,常智,朱仕军.混合相位动态子波估计[J].油气地球物理,2008,6(1):21-24

Peng C,Zeng T,Chang Z,et al.Estimation of mixed-phase nonstationary wavelet [J].Petroleum Geophysics,2008,6(1):21-24

[5] Mirko van der B.Time-varying wavelet estimation and deconvolution by kurtosis maximization [J].Geophysics,2008,73(2):11-18

[6] 高静怀,汪玲玲,赵伟.基于反射地震记录变子波模型提高地震记录分辨率[J].地球物理学报,2009,52(5):1289-1300

Gao J H,Wang L L,Zhao W.Enhancing resolution of seismic trances based on the changing wavelet model of the seismogram [J].Chinese Journal of Geophysics,2009,52(5):1289-1300

[7] 冯晅,刘财,杨宝俊,等.分时窗提取地震子波及在合成地震记录中的应用[J].地球物理学进展,2002,17(1):71-77

Feng X,Liu C,Yang B J.The extractive method of seismic wavelet in different time window and the application in synthetic seismogram [J].Progress in Geophysics,2002,17(1):71-77

[8] 高静怀,陈文超,李幼铭，等.广义S变换与薄互层地震响应分析[J].地球物理学报,2003,46(4):526-532

Gao J H,Chen W C,Li Y M,et al.Generalized S transform and seismic response analysis of thin interbeds [J].Chinese Journal of Geophysics,2003,46(4):526-532

[9] Stockwell R G.A basis for ef digital signal processing of the S-transform [J].Digital Signal Processing,2006:1-22

[10] Ervin S, Djurovi L, Jin J. A window width optimized S-transform[J]. EURASIP Journal on Advances in Signal Processing,28(1):1-13

[11] 齐春艳,李彦鹏,彭继新,等.一种改进的广义S变换[J].石油地球物理勘探，2010,45(2):215-218

Qi C Y,Li Y P,Peng J X,et al.An improved generalized S-transform [J].Oil Geophysical Prospecting,2010,45(2):215-218

[12] 张贤达.现代信号处理[M].第2版.北京：清华大学出版社,2002:360-362

Zhang X D.Modern signal processing [M].2nd ed.Beijing:Tsinghua University Press,2002:360-362

[13] Tian J,Song W,Yang F.Enhancing the resolution of seismic data based on the generalized S-transform [J].Petroleum Science,2009,6:153-157

[14] 高静怀,张兵.基于时频滤波的吸收衰减参数估算[J].石油地球物理勘探,2012,47(6):931-936

Gao J H,Zhang B.Seismic attenuation parameter estimation based on the time-frequency filtering [J].Oil Geophysical Prospecting,2012,47(6):931-936

[15] Rosa A L，Ulrych T J.Processing via spectral modeling [J].Geophysics.1991,56(8):1244-1251

[16] 孙成禹.谱模拟方法及其在提高地震资料分辨率中的应用[J].石油地球物理勘探,2000,35(1):27-35

Sun C Y.Spectrum modeling method and its application to seismic resolution improvement [J].Oil Geophysical Prospecting,2000,35(1):27-35

[17] 唐博文,赵波,吴艳辉,等.一种实现谱模拟反褶积的新途径[J].石油地球物理勘探,2010,45(增刊1):66-70

Tang B W,Zhao B,Wu Y H,et al.A new method for spectral-modeled deconvolution [J].Oil Geophysical Prospecting,2010,45(S1):66-70