脉冲中子源密度测井俘获伽马射线强度的数值模拟
2014-03-25潘保芝蒋必辞
潘保芝,张 瑞,刘 坤,李 丁,蒋必辞
(1.吉林大学地球探测科学与技术学院,吉林长春130026;2.中国石油大学(华东)地球科学与技术学院,山东青岛266580)
为取代传统密度测井中的同位素中子源,各大石油公司都在研究利用脉冲中子源测量地层密度的方法。脉冲中子源是一个小型的加速器,将氘核加速轰击锆氚靶上的氚核,通过聚变反应产生快中子[1]。脉冲中子源以一定的脉冲宽度和重复周期向地层发射能量为14MeV的中子束。与常规中子源相比,脉冲中子源具有源强度高且质量轻、释放出的中子能量单一等特点,特别是能够依赖电信号以脉冲的形式向外界发射中子,而当电信号停止,中子便不再发射,故没有放射性危害。
关于脉冲中子源密度测量的研究,已经取得一定的成就。1997年,康普乐公司首先研制出了利用快中子非弹散射伽马射线获取地层密度的测井仪器[1];2005年,斯伦贝谢公司推出了包括脉冲中子密度测井在内的随钻测井平台[2-3];2013年Atfeh等[4]利用脉冲中子源密度测井方法对大规模碳酸盐岩储层进行了实例研究,进一步证明了脉冲中子源方法进行地层评价的可用性。
前人对于脉冲中子源密度测井的研究,大多以非弹散射伽马射线为研究对象,目前相关理论已基本成熟。本文的研究对象是俘获伽马射线,将俘获伽马射线作为密度测井的伽马源进行研究,模拟分析经地层吸收后剩余伽马射线强度与地层密度以及探测源距的关系,从而指导脉冲中子源密度测井仪器的设计。
蒙特卡洛数值模拟方法是模拟微观粒子运输的重要工具,在核测井方面有很大的应用价值。它成本低,周期短,并在一定程度上弥补了无法获得实体物理模型的缺陷[5]。我们采用蒙特卡洛数值模拟方法模拟并记录粒子的轨迹,得到中子与原子核碰撞以及扩散后的位置,研究中子被俘获产生的俘获伽马射线强度的分布,分析经地层吸收后剩余伽马射线强度与地层密度的关系,并讨论测量条件对剩余伽马射线强度分布的影响。
1 模拟原理及建立模型
脉冲中子源发射的快中子进入地层后,依次发生减速作用损失能量以及扩散作用后被俘获[6]。发生减速作用和被俘获时分别产生非弹散射伽马射线和俘获伽马射线。我们将产生的俘获伽马射线作为密度测井的伽马源,该伽马射线进入地层后,会被地层衰减,部分被吸收,通过模拟经地层吸收后剩余伽马射线的强度,便可以得出其强度与地层密度的关系。
首先建立一个各向同性均匀二维介质平面模型,为了使效果更直观清楚,采用直角坐标系研究极坐标问题,将中子源设定在坐标原点(0,0),模拟范围为200cm×200cm,骨架是石英,孔隙度(φ)可变,孔隙流体是含氯(Cl)的矿化水。脉冲中子源发射大量的快中子,假设快中子进入地层时的初始能量为14MeV,不考虑最初的非弹散射,快中子与孔隙中的流体或者岩石的骨架发生弹性碰撞,其能量逐渐减弱,变成热中子,之后经过扩散作用,最后被地层中的核素俘获并产生俘获伽马射线。大量的俘获伽马射线进入地层之后,经康-吴效应和光电效应将被地层吸收一部分,最终得到剩余伽马射线的分布。图1为用俘获伽马射线的衰减探测地层密度示意图。

图1 用俘获伽马射线的衰减探测地层密度示意图解
2 中子与物质作用过程的模拟
2.1 减速过程的模拟
脉冲中子源发射的快中子,依次经过地层的减速作用和扩散作用而被地层核素俘获。首先模拟地层对快中子的减速作用过程。不考虑最开始的非弹散射,只模拟弹性散射减速作用。而减速作用主要是地层中的氢核素(H)引起的,所以只考虑与孔隙中H的弹性碰撞过程。快中子弹性碰撞过程中能量的变化为
(1)
式中:E0表示碰撞前的能量;E′表示碰撞后的能量;M为靶核的质量;m为快中子的质量;θ为弹性散射角度。
对于大量快中子的模拟,建立分别表示x坐标、y坐标和能量E的3个二维数组xij,yij和Eij,数组下标表示第i个快中子的第j次碰撞;为了获得足够数量的计算,用new(·)函数将数组定义为动态的,用rand(·)函数产生随机数赋给每一个散射角度,两次碰撞之间的路程为1cm[7],初始能量为14MeV,终止能量为热中子能量0.025eV。
模拟了中子数量N=1000时不同孔隙度情况下热中子的分布(图2),图2a,图2b和图2c分别是地层孔隙度为5%,40%,100%(水)时1000个热中子的初始位置云图。从图2中可以看出,热中子是围绕中子源呈圆形分布的,在离源近的地方分布较密集,离源远的地方分布较稀疏;热中子云的半径随介质孔隙度的增大而逐渐减小,这是因为在减速过程中,H是最重要核素,含氢指数越大,快中子越容易被减速。由于H主要出现在油或水中,所以在地层中不含泥或不含结晶水的情况下,可以通过脉冲中子测井研究地层中的含氢量,从而求取孔隙度。通过热中子云的半径来判断介质的减速长度,由图2c可得水的减速长度约为7.5cm,这刚好与实际查得的资料相符,实际查阅水的减速长度为7.7cm[6]。

图2 不同地层孔隙度条件下热中子的初始位置云图(N=1000)
2.2 扩散过程和俘获过程的模拟

(2)
式中:∑a与∑s分别为介质的宏观俘获截面和宏观散射截面。已知水的∑a=0.0220cm-1,∑s=2.6800cm-1;石英的∑a=0.0034cm-1,∑s=0.2680cm-1[6]。在得到每个热中子的初始位置之后,热中子要在介质中扩散,扩散的距离由(2)式计算。扩散的角度随机,用rand(·)函数生成1~100的随机数,当随机数小于孔隙度时,认为热中子在水中扩散,当随机数大于孔隙度时,认为热中子在石英中扩散。图3和图4分别显示了孔隙度为20%和50%时扩散前、后的1000个热中子位置云图。
由图3和图4可以看出,热中子扩散使得中子云半径增大,孔隙度越大,热中子扩散长度越小。这是因为当孔隙度增大时,岩石骨架含量相应减少,骨架的热中子扩散长度比孔隙水的热中子扩散长度大,所以综合结果导致热中子扩散长度减小。

图3 地层孔隙度为20%时扩散前(a)、后(b)的热中子位置云图(N=1000)
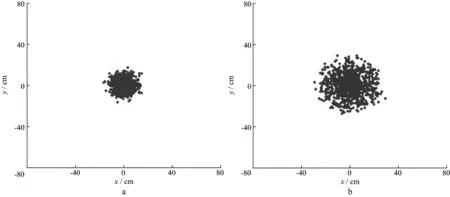
图4 地层孔隙度为50%时扩散前(a)、后(b)的热中子位置云图(N=1000)
热中子扩散结束即被核素俘获同时产生俘获伽马射线,对于几种常见的核素来说,除了H核素之外,氯(Cl)、硅(Si)、铝(Al)、钙(Ca)俘获热中子产生的伽马射线能量相差并不大,都在7MeV左右[6]。所以模拟时将放出的伽马射线能量定为7MeV。这些俘获伽马射线便可作为密度测井的“伽马源”。
在这些核素中,氧(O)的俘获截面与其它核素相比低很多[6],故将O的俘获作用省略,只模拟H,Cl和Si。依然模拟一个岩石骨架为石英的纯地层,而孔隙流体为具有一定矿化度的水,将被3种不同核素俘获的热中子位置分别进行统计,得到其热中子俘获位置云图。图5是孔隙度为20%,氯含量占孔隙体积的百分比(VCl)为10%时,1000个热中子被Cl,Si,H俘获的位置云图。图5中被Cl俘获放出的伽马射线最多,Si次之,而H最少,这是因为三者的俘获截面不同以及含量不同所引起的。

图5 热中子被Cl,Si,H俘获的位置云图(φ=20%,%,N=1000)
3 俘获伽马射线吸收过程的模拟
3.1 俘获伽马射线强度分布的模拟
已知热中子被Cl和Si俘获产生两种能量的伽马量子,被H俘获产生一种伽马量子[6],所以可以计算这个“伽马源”的强度。将热中子被俘获的区域进行网格划分,每个网格大小为5cm×5cm,求出每个单位面积内的伽马量子数,统计得出俘获伽马射线的强度分布。为了找出更准确的统计规律,将中子数量增加到10000个进行模拟。图6分别是孔隙度为5%,10%和20%时10000个热中子产生的俘获伽马射线强度(Q)分布图,这些也就是分散式的伽马源。
由图6可以看出,俘获伽马射线强度在中子源附近较大,随着与中子源的距离L的增大,伽马射线强度迅速减弱。并且,孔隙度小的地层伽马射线强度分布较平缓,峰值较小;孔隙度大的地层伽马射线强度分布较陡峭,峰值较大。即孔隙度越大,俘获伽马射线强度随源距下降得越快。

图6 不同孔隙度条件下10000个热中子俘获伽马射线强度分布图解
对图6选取y=0,x>0的剖面进行绘图,结果如图7所示。从图7中可以看出,俘获伽马射线强度随源距L的增大而降低。当L>100cm时,俘获伽马射线强度已经趋近于零;当L≈35cm时,对于不同孔隙度的地层俘获伽马射线强度几乎交于一点,此时俘获伽马射线强度与地层孔隙度无关;当L<35cm时,孔隙度高的地层俘获伽马射线强度大;当L>35cm时,孔隙度低的地层俘获伽马射线强度大。

图7 10000个热中子俘获伽马射线强度随源距的变化
3.2 俘获伽马射线吸收过程的模拟
俘获伽马射线进入地层后,会被地层中的元素吸收,已知剩余伽马射线强度J满足如下关系式[6]:
(3)
式中:i表示面积单元序号;Qi表示第i个单元内俘获放出的伽马射线强度;ri表示第i个单元到探测点的距离;n表示单元的总个数;μm为质量吸收系数;ρ为地层密度。
模拟时首先进行网格划分,共划分成1600个5cm×5cm的网格,即n=1600。统计每个网格内的俘获伽马射线个数Qi,将质量吸收系数μm设定为0.17cm2/g[6]。假设地层孔隙度分别为5%,10%,20%,30%,40%,对于每一个孔隙度都分别假设地层密度为2.1,2.2,2.3,2.4,2.5g/cm3,统计在0,10,20,30,……,140cm源距处的剩余伽马射线强度,从而得出其在纵向上的分布。图8为剩余伽马射线强度随孔隙度变化(ρ=2.4g/cm3)和随密度变化(φ=5%)的分布。
从图8a可以看出,当L≈55cm时,剩余伽马射线强度不受孔隙度的影响;当L<55cm时,剩余伽马射线强度随孔隙度的增大而增大;当L>55cm时,剩余伽马射线强度随孔隙度的增大而减小。从图8b中可以看出,剩余伽马射线强度随密度的增高而减小。
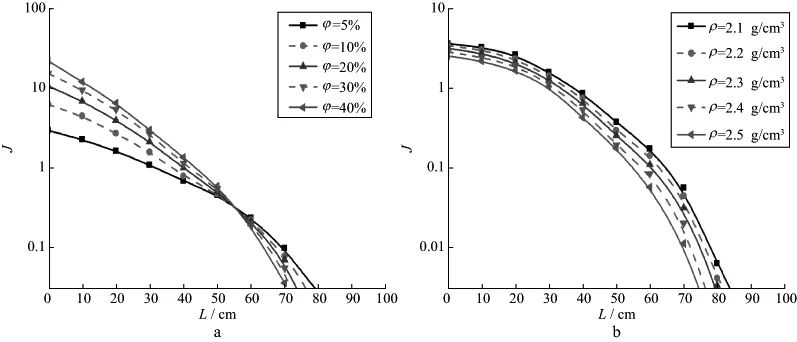
图8 10000个热中子产生的剩余伽马射线强度随孔隙度变化(ρ=2.4g/cm3)(a)和随密度变化(φ=5%)(b)的分布
3.3 剩余伽马射线强度与地层密度的关系
设计脉冲中子源密度测井仪器时,其中一个最重要的参数就是源距L。伽马探测器所放的位置,既要保证探测器的计数率较高又要保证反映地层密度的精度达到一定的需求。由3.2节中的模拟结果可知,在L≈55cm位置处,剩余伽马射线强度不受孔隙度的影响,且对密度变化比较敏感,所以源距L最好选择在50~60cm。
由3.1节中的模拟结果可知,在源距为50~60cm处,俘获伽马射线强度随孔隙度的增大而减小,其变化关系如图9a所示。由图9a可见,俘获伽马射线强度与孔隙度φ呈指数关系。而由公式(3)可推知剩余伽马射线强度J与孔隙度φ之间也呈指数关系。
选中源距为50~60cm之后,得到不同孔隙度条件下的剩余伽马射线强度与密度的关系,其中L=55cm处的剩余伽马射线强度与密度的关系曲线示于图9b。使用模拟的数据进行拟合,得到剩余伽马射线强度与地层密度、孔隙度以及源距的拟合关系为
(4)
其相关系数为0.97。需要说明的是,此关系式为每万个中子产生的剩余伽马射线强度,中子源能量为14MeV。在实际应用中,(4)式中的孔隙度φ为同一个仪器中子探测部分所获得的孔隙度。

图9 特定源距时俘获伽马射线强度Q与孔隙度φ的关系(a)和剩余伽马射线强度J与密度ρ的关系(b)
3.4 剩余伽马射线强度的影响因素
3.4.1 中子源强度N和能量E的影响
中子源的特性对剩余伽马射线强度有着一定的影响,评价中子源的特性主要从源强度N和源能量E两个方面考虑。图10a是中子源强度对剩余伽马射线强度影响(E=14MeV,φ=5%,VCl=10%,ρ=2.4g/cm3)的模拟结果,可以看出剩余伽马射线强度随中子源强度N的增大而增大。这是因为当中子源的强度增大时,与核素反应的中子数增加,产生的俘获伽马射线数量增大,从而剩余伽马射线强度增加。图10b是中子源能量对剩余伽马射线强度影响(N=10000,φ=5%,VCl=10%,ρ=2.4g/cm3)的模拟结果,可以看出中子源的能量E对剩余伽马射线强度几乎没有影响。

图10 中子源强度(a)、中子源能量(b)和地层水含氯量(c)对剩余伽马射线强度影响的模拟分析
3.4.2 地层水含氯量(VCl)的影响
氯是最重要的热中子俘获物质,俘获截面大且放出的伽马射线数量多,所以地层水中氯的含量对剩余伽马射线强度有一定的影响,但影响不大。图10c 为地层水含氯量对剩余伽马射线影响(E=14MeV,N=10000,φ=5%,ρ=2.4g/cm3)的模拟结果。由图10c可以看出,在源距选定之后,随着水中含氯量的增大,剩余伽马射线的强度也增大。这是因为含氯量增大使得中子与核素作用总的宏观俘获截面增加,产生的俘获伽马射线强度增大,从而剩余伽马射线强度也随之增大。
4 结论与认识
1) 脉冲中子源发射的快中子经地层减速作用产生的热中子,以中子源为中心呈圆形分布;当地层孔隙度增大时,热中子分布半径变小。热中子扩散作用导致热中子云的半径有所增大,而且随着孔隙度的增加,热中子的扩散长度减小。
2) 俘获伽马射线强度随源距L的增大呈指数迅速降低。且当L>100cm时,俘获伽马射线强度几乎为零;当L≈35cm时,俘获伽马射线强度与孔隙度无关;当L<35cm时,孔隙度大的地层俘获伽马射线强度大;当L>35cm时,孔隙度小的地层俘获伽马射线强度大。
3) 俘获伽马射线经过地层吸收之后,得到的剩余伽马射线强度受孔隙度和地层密度的共同影响,随密度的增加而减小;合适的源距为50~60cm,建立了剩余伽马射线强度与地层密度、孔隙度以及源距的拟合关系,可以指导脉冲中子源密度测井仪器的设计。
4) 中子源强度、地层水含氯量对剩余伽马射线强度也有影响,剩余伽马射线强度随中子源强度和地层水含氯量的增大而增大;而中子源能量对剩余伽马射线强度几乎没有影响。
参 考 文 献
[1] 于华伟,孙建孟,朱文娟,等.随钻脉冲中子密度测井的蒙特卡罗模拟研究[J].测井技术,2009,33(6):521-524
Yu H W,Sun J M,Zhu W J,et al.Monte-Carlo simulation method in pulsed neutron density logging while drilling[J].Well Logging Technology,2009,33(6):521-524
[2] Reichel N,Evans M,Allioli F,et al.Neutron-gamma density(ngd):principles,field test results and log quality control of a radioisotope-free bulk density measurement[J].SPWLA 53rdAnnual Logging Symposium, 2012,GGG
[3] Quirein J A,Jr H S,Chen D D,et al.Formation density prediction using pulsed neutron capture tools[J].SPWLA 46thAnnual Logging Symposium,2005,QQ
[4] Atfeh M,Daghar K A A,Marzouqi K A,et al.Neutron porosity and formation density acquisition without chemical sources in large carbonate reservoirs in the middle east-a case study[J].SPWLA 54thAnnual Logging Symposium,2013,KKK
[5] 吴文圣.Monte Carlo方法在核测井中的新应用[J].测井技术,2001,25(6):412-416
Wu W S.The uses of Monte Carlo method in nuclear logging[J].Well Logging Technology,2001,25(6):412-416
[6] 李舟波.钻井地球物理勘探 [M].北京:地质出版社,2006:114-175
Li Z B.Geophysical exploration drilling [M].Beijing:Geological Publishing Press,2006:114-175
[7] 庞巨丰.核测井物理基础[M].北京:石油工业出版社,2005:94-129
Pang J F.Physical basis of nuclear logging [M].Beijing:Petroleum Industry Press,2005:94-129
[8] 于华伟.随钻环境下脉冲中子测量地层密度的理论基础研究[D].青岛:中国石油大学(华东),2011
Yu H W.The fundamental research of the pulsed-neutron density logging while drilling[D].Qingdao:China University of Petroleum,2011
[9] Odom R C,Bailey S M,Wilson R D,et al.Pulsed neutron density measurements:modeling the depth of investigation and cased-hole wellborge uncertainties[J].SPWLA 40thAnnual Logging Symposium,1999,JJ
