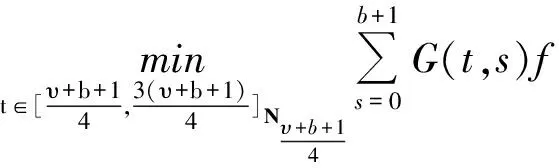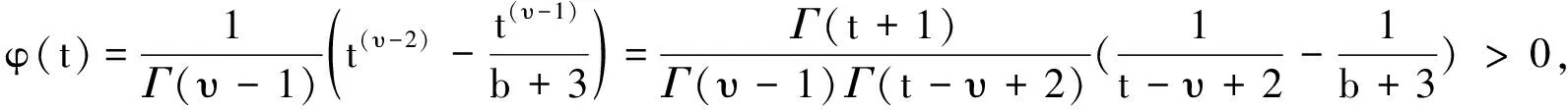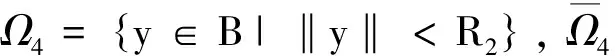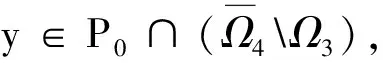一类分数阶差分方程正解的存在性
2014-03-25祝相宇孙明哲
祝相宇, 孙明哲
( 延边大学理学院 数学系, 吉林 延吉 133002 )
近年来,差分方程被广泛应用于机械系统、经济等研究领域中,并逐步成为了一个独立的理论体系.目前为止,关于有限分数阶差分问题的研究成果还较少.其中: Miller和Ross[1]将线性有序的υ阶分数阶微分方程作为一般的整数阶线性有序分数阶微分方程的模型来考虑问题,并取得了一些有意义的成果.文献[2]采用一种改进的方法来求解了该类问题;文献[3]研究了上述问题的一种适定的初始值问题,并给出了多种解决算法.本文在借鉴前人研究方法的基础上,对一类有限分数阶非线性差分方程边值问题正解的存在性进行研究,获得了该类问题存在正解的充分性条件.
本文中考虑的有限分数阶差分方程边值问题为:
-Δυy(t)=f(t+υ-1,y(t+υ-1)),t=1,2,3,…,b+1;
(1)
y(υ-3)=0,y(υ+b+1)=0,y(υ-2)=g(y).
(2)
其中 2<υ≤3,b是整数且满足b≥2,f∶[υ-1,υ+b]Nυ-1×R→R是连续函数.记
Η={(y(υ-3),y(υ-2),…,y(υ+b+1))Τ|y(υ+i-3)∈R,i=0,1,2,…,b+4}.
g∶Η→R是给定的映射.
为方便,本文记Na={a,a+1,a+2,…}, [a,b]Na={a,a+1,a+2,…,b}, 其中b-a∈N1.
1 预备知识
定义1[4]对于υ>0, 定义函数f的υ阶分数和为
定义2[4]对于N∈N, 0≤N-1<υ≤N, 定义函数f的υ阶分数差分为
Δυf(t)=ΔNΔυ-Nf(t),t∈Na+N-υ.

引理1[4]对于∀t,υ∈R, 如果t(υ),t(υ-1)都有定义,那么Δt(υ)=υt(υ-1).
引理2[5]设f是定义在Na上的实函数,令μ,υ>0, 则有
Δ-υ(Δ-μf(t))=Δ-(υ+μ)f(t)=Δ-μ(Δ-υf(t)),t∈Na+μ+υ.
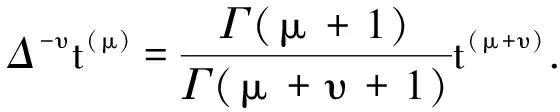
引理4[5]对于任意的实数υ和任意的正整数P, 有

引理5[4]令0≤N-1<υ≤N,ci∈R,i=1,2,3,…,N, 方程Δυy(t)=0有N个线性无关的解,其解可以表示为y(t)=c1t(υ-1)+c2t(υ-2)+…+cNt(υ-N), 且有Δ-υΔυy(t)=y(t)+c1t(υ-1)+c2t(υ-2)+…+cNt(υ-N).

(i) ‖Ax‖≤‖x‖,∀x∈P∩∂Ω1; ‖Ax‖≥‖x‖,∀x∈P∩∂Ω2.
(ii) ‖Ax‖≥‖x‖,∀x∈P∩∂Ω1; ‖Ax‖≤‖x‖,∀x∈P∩∂Ω2.
引理7[5]设υ是任意正实数,a和b是两个实数且有x (ii) (a-x)(υ)/(b-x)(υ)是关于x的递减函数,其中x∈[0,a-υ)N. 构造带有边值条件(2)的分数阶差分方程 -Δυy(t)=h(t+υ-1),t=1,2,3,…,b+1, 2<υ≤3 (3) 的Green函数,其中h∶[υ-1,υ+b+1]Nυ-1→R是连续的. 定理1设2<υ≤3,g∶Rb+5→R, 则分数阶差分方程(3)及(2)式有唯一解: (4) 定理2Green函数G(t,s)具有以下性质: (i)G(t,s)>0, (t,s)∈[υ-1,υ+b+1]Nυ-1×[0,b+1]N0; (ii) maxt∈[υ-1,υ+b+1]Nυ-1G(t,s)=G(s+υ-1,s), 其中s∈[0,b+1]N0; (iii) 存在γ∈(0,1), 使得 即G(t,s)>0.因此,结论(i)成立. (iii)易知 由定理1知,求分数阶差分方程(1)和(2)的解等价于在(2)式条件下求解求和方程 (5) 的解,其中t∈[υ-1,υ+b+1]Nυ-1. 定义Banach空间 B={y∶[υ-3,υ+b+1]Nυ-3→R|y(υ-3)=y(υ+b+1)=0,y(υ-2)=g(y)}, (6) 并赋范数为‖y‖=max|y(t)|,t∈[υ-3,υ+b+1]Nυ-3. 引理8若g(y)≥0, 则存在常数γ′∈(0,1)使得 引理9假设条件①成立,那么对于∀y∈p有Ay∈P0; 特别的,算子A是锥P0到P0上的映射. 定理3(i)假设条件①和②成立,那么分数阶差分方程(1)和方程(2)至少有一个非零解y∈P0; (ii) 假设条件①和③成立,那么分数阶差分方程(1)和方程(2)至少有一个非零解y∈P0. (7) 对于Ω4的构造,按以下两种情况来考虑: MKH(b+2) (8) (9) 设Ω4={y∈B∶‖y‖ 参考文献: [1] Miller K S, Ross B. Fractional difference calculus[C]//Procedings of the internations symposium on univalent functions. Koriyama: Fractional Calculus and Their Applications Nihon University, 1988:139-152. [2] Atici F M, Eloe P W. A transform method in discrete fractional calculus[J]. Int J Difference Equ, 2007,2(2):165-176. [3] Atici F M, Eloe P W. Initial value problems in discrete fractional calculus[J]. Proc Amer Math Soc, 2009,137:981-989. [4] Goodrich C S. Existence and uniqueness of solutions to a fractional difference equation with nonlocal conditions[J] . J Comput Math Appl, 2011,61(21):191-202. [5] Atici F M, Eloe P W. Two-point boundary value problems for finite fractional difference equations[J]. J Difference Equ Appl, 2011,17(4):445-456. [6] Zhao Yige, Sun Shurong,Han Zhenlai. The existence of multiple positive solutions for boundary value problems of nonlinear fractional differential equations[J]. J Commun Nonlinear Sci Number Simulat, 2011(16):2086-2097. [7] 时宝,张德存,盖久明.微分方程理论及其应用[M].北京:国防工业出版社,2005:13. [8] 程金发.分数阶差分方程理论[M].厦门:厦门大学出版社,2010. [9] Chen F Q. Extreme solutions of initial value problems for nonlinear second order integrodifferential equations in Banach spaces[J]. Acta Math Appl Sinica, 2001,17:289-298.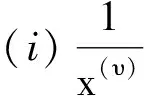
2 Green函数及其性质
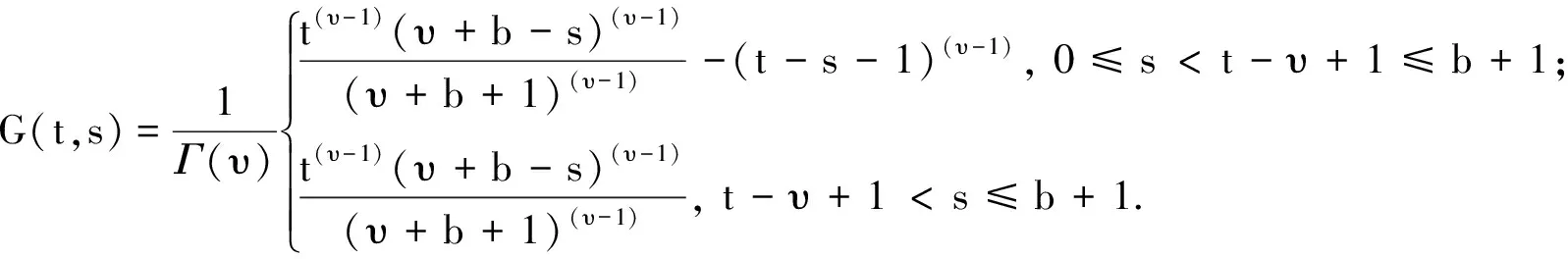

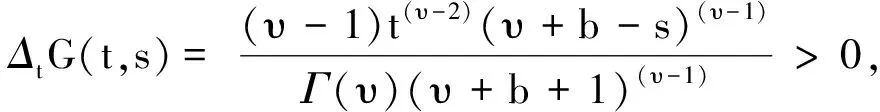


3 正解的存在性