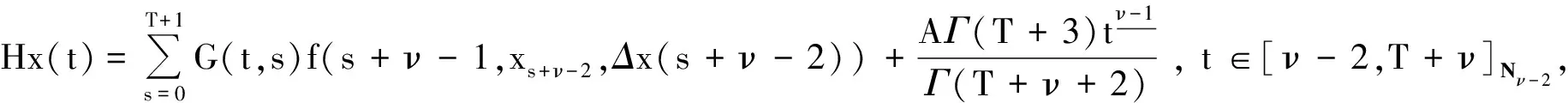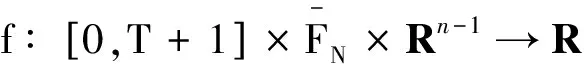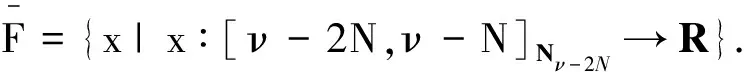一类分数阶泛函差分边值问题解的存在性

吴双， 慎闯， 侯成敏

( 延边大学理学院 数学系， 吉林 延吉 133002 )

差分方程广泛应用于各领域，如计算机科学、动力系统、机械系统及经济系统等.近年来，由于分数阶差分方程模型的不断出现以及对微分方程近似计算的需要,分数阶差分方程逐渐成为学者们关注的研究课题，其基础理论也得到了进一步的发展.例如：文献[1-2]分别研究了离散型分数阶微积分初值问题和有限分数阶差分方程的两点边值问题； C.S.Goodrich[3]研究了带有非局部条件的离散型分数阶边值问题解的存在性和唯一性；文献[4-5]分别对正定非线性项的差分边值问题进行了研究，得到了正定差分边值问题正解的存在性；文献[6-7]分别对非线性项具有混合单调性的差分方程正解的存在性进行了研究.Miller 和Ross[9]最先对有限分数阶差分问题进行了研究，但目前为止，相关结果并不多.最近，文献[10]的作者进一步研究了有限分数阶差分问题，并提供了一种改进的方法.本文将对一类分数阶泛函差分方程边值问题(1)—(3)的解的存在性进行研究.

本文考虑如下的离散分数阶方程边值问题：

Δνx(t)=f(t+ν-1，xt+ν-2,Δx(t+ν-2)),t∈[0,T+1]N0；

(1)

x(s+ν-2)=φ(s+ν-2),s∈[-N，0]N-N；

(2)

x(T+ν+1)=A.

(3)

其中f∶[ν-1,T+ν]Nν-1×FN×R→R是连续的，且φ∈FN,FN={x|x∶[-N+ν-2,ν-2]N-N+ν-2→R}, 1<ν<2,A∈R.

1 预备知识

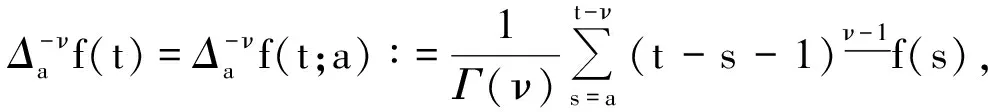
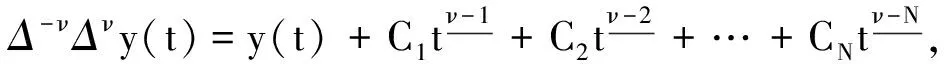
引理2[2]令C为一个带有模的线性空间E的凸子集，并设0∈C; 设F∶C→C是一个完全连续的算子，并令ε(F)={x∈C|x=λFx,∀λ∈(0,1)}, 则ε(F)是无界的，或者F有一个不动点.

2 主要结果及其证明

定理1设f∶[0,T+1]N0×FN×R→R, 则函数x(t)是差分方程(1)带有边界条件(2)和(3)的解的充要条件是x(t)有以下形式：

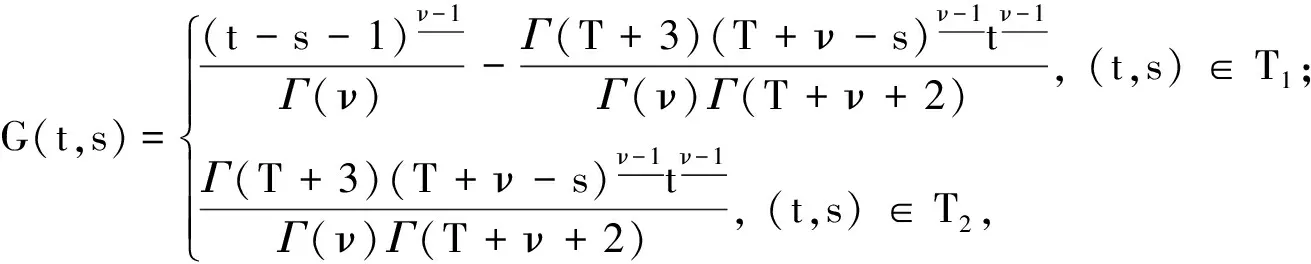
T1={(t,s)∈[ν-2,T+ν+1]Nν-2×[0,T+1]N0:0≤s

T2={(t,s)∈[ν-2,T+ν+1]Nν-2×[0,T+1]N0:0≤t-ν+1≤s≤T+2}.

定义变换S如下：

定理2令f∶[0,T+1]×FN×R→R是连续的，若对于任意的0<λ<1, 存在M>0, 使对于满足条件(5)和(6)的方程(4)的解x, 有‖x‖[ν-2,T+ν+1]Nν-2≤M, 则边值问题(1)—(3)至少有一个解.

Δνx(t)=λf(t+ν-1，xt+ν-2,Δx(t+ν-2))，t∈[0,T+1]N0;

(4)

x(s+ν-2)=φ(s+ν-2)，s∈[-N，0]N-N;

(5)

x(T+ν+1)=λA.

(6)

证明当λ=0时，边值问题(4)—(6)即为(1)—(3).不妨设λ≠0, 则证明过程分为φ(ν-2)=0和φ(ν-2)≠0两种情况.

2) 当φ(ν-2)≠0时,令y=x-φ(ν-2), 那么

(7)

(8)

(9)

下面讨论高阶离散分数阶方程边值问题(10)—(12)，其中N-1<ν

Δνx(t)=f(t+ν-N+1，xt+ν-N,…,ΔN-1x(t+ν-N)) ，t∈[0,T+1]N0；

(10)

x(s+ν-N)=φ(s+ν-N) ，s∈[-N，0]N-N;

(11)

Δix(T+ν+3-N)=Ai，i=0,1,2,…,N-2.

(12)

类似于定理2，得以下定理：

Δνx(t)=λf(t+ν-N+1，xt+ν-N,…,ΔN-1x(t+ν-N))，t∈[0,T+1]N0;

(13)

x(s+ν-N)=φ(s+ν-N)，s∈[-N，0]N-N;

(14)

Δix(T+ν+3-N)=λAi，i=0,1,2,…,N-2.

(15)

证明先求解边值问题(10)—(12)，由引理1知其解为

(16)

参考文献：

[1] Atici F M, Eloe P W. Initial value problems in discrete fractional calculus[J]. Proc Amer Math Soc, 2009,137(3):981-989.

[2] Atici F M, Eloe P W. Two-point boundary value problems for finite fractional difference equations[J]. J Difference Equ Appl, 2011,17(4):445-456.

[3] Goodrich C S. Existence and uniqueness of solutions to a fractional difference equation with nonlocal conditions[J]. J Comput Math Appl, 2011,61(21):191-202.

[4] Li W T, Niu M F, Sun J P. Existence of positive solutions of boundary value problems for second-order nonlinear difference systems[J]. Appl Math Comp, 2004,152:779-798.

[5] Sun J P, Li W T. Existence of positive solutions of boundary value problems for a discrete difference system[J]. Appl Math Comp, 2004,156:857-870.

[6] Chen F Q. Existence of solutions for mixed monotone impulsive volterra integral equations in Banach spaces[J]. Acta Math Sci, 1998,18:371-378.

[7] Chen F Q. Extreme solutions of initial value problems for nonlinear second order integro differential equations in Banach spaces[J]. Acta Math Appl Sinica, 2001,17:289-298.

[8] Atici F M, Eloe P W. Initial value problems in discrete fractional calculus[J]. Proc Amer Math Soc, 2009,137:981-989.

[9] Miller K S, Ross B. An introduction to the fractional calculus and fractional differential equations[M]. New York： Wiley, 1993.

[10] Atici F M, Eloe P W. A transform method in discrete fractional calculus[J]. Int J Difference Equ, 2007,2(2):165-176.